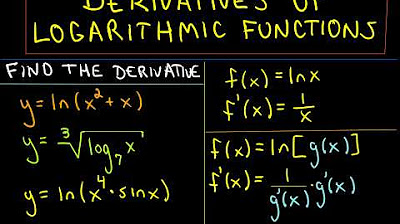Math 11 - Section 2.3
TLDRThe video script is a comprehensive calculus lesson focusing on the derivatives of logarithmic functions, specifically the natural logarithm (ln). The instructor begins by stating the derivative of ln(x) is 1/x and emphasizes the importance of the chain rule when dealing with more complex logarithmic expressions. Several examples are worked through, including the use of the chain rule in functions like ln(x^2 + 1) and applications of the product and quotient rules in expressions involving logarithms. The script also covers the differentiation of logarithms with respect to different bases and the use of logarithmic properties to simplify derivatives. The lesson concludes with applications of these concepts, such as modeling consumer response to advertising and calculating the time needed to warm a frozen package to a certain temperature. The instructor highlights the importance of understanding both the mathematical process and the practical implications of the calculations.
Takeaways
- 📚 The derivative of the natural logarithm function ln(x) with respect to x is 1/x.
- 🔑 Remember to apply the chain rule when differentiating composite functions, such as ln(x^2 + 1), which results in (1/(x^2 + 1)) * (2x).
- 📈 For a constant multiplied by a logarithm, such as -8 ln(x), the derivative keeps the constant multiple and multiplies by the derivative of ln(x), resulting in -8/x.
- ⛓ Use the product rule for functions that are a product of two variables, like x^4 * ln(x), which involves multiplying the first by the derivative of the second and vice versa, then simplifying.
- 🗒️ When differentiating a quotient, such as ln(x) / x^4, apply the quotient rule: (bottom * derivative of top - top * derivative of bottom) / (bottom)^2.
- 🔗 The derivative of ln(6x) can be broken down using logarithm properties into ln(6) + ln(x), where the derivative of ln(6) is zero, leaving 1/x after simplification.
- ⏱️ For applications, such as advertising models, use derivatives to find rates of change, like additional units sold per thousand dollars spent on advertising.
- 📉 As advertising spending (a) increases, the rate of additional units sold (n'(a)) decreases, eventually leading to a point of diminishing returns where further advertising spending does not result in more sales.
- 🧮 When solving for specific values, like t'(60) in a warming problem, use the derivative to find the rate of change at that point, which represents minutes per degree in this context.
- 🍲 In the context of warming a frozen package, the derivative t'(t) can be used to estimate the time it takes for the temperature to increase by an additional degree at a specific time point.
- 🔍 Always check the units and the context when performing derivative calculations to ensure the results make sense in the real-world scenario, such as time in minutes and temperature in degrees Fahrenheit.
Q & A
What is the derivative of ln(x) with respect to x?
-The derivative of ln(x) with respect to x is 1/x.
What is the derivative of ln(x^2 + 1) using the chain rule?
-The derivative of ln(x^2 + 1) is (1/(x^2 + 1)) * (2x), which simplifies to 2x/(x^2 + 1).
How is the constant multiple rule applied when differentiating y = -8ln(x)?
-The derivative of y = -8ln(x) is found by multiplying the constant -8 with the derivative of ln(x), which is 1/x, resulting in -8/x.
What is the derivative of f(x) = ln(6x) using the properties of logarithms?
-Using the property of logarithms that allows us to split the argument as ln(6) + ln(x), the derivative of f(x) = ln(6x) is 1/x, since ln(6) is a constant and its derivative is 0.
Explain the application of the product rule in the given script when differentiating y = x^4 * ln(x).
-The product rule states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first. For y = x^4 * ln(x), the derivative is (x^4)(1/x) + (4x^3)(ln(x)), which simplifies to x^3 + 4x^3ln(x).
What is the quotient rule and how is it applied in the script?
-The quotient rule states that the derivative of a quotient of two functions is (high' * low - high * low') / (low)^2. In the script, it is applied when differentiating ln(x) / x^4, resulting in (1/x - ln(x) * 4x^3) / (x^8).
How is the limit of n'(a) as a approaches infinity discussed in the script?
-The limit of n'(a) as a approaches infinity is discussed by analyzing the behavior of the derivative as the advertising spend 'a' increases. It is shown that as 'a' gets larger, the additional units sold per thousand dollars of advertising decreases, eventually reaching a point where it doesn't make sense to spend more on advertising due to diminishing returns.
What is the formula given for the time needed to warm a frozen package of smoked salmon?
-The formula given for the time needed to warm a frozen package of smoked salmon to a certain temperature in Fahrenheit is t = 250 * ln((38)/(76 - t)), where t is the time in minutes.
How is the concept of logarithmic differentiation applied to the function y = ln(x^4/2)?
-The concept of logarithmic differentiation is applied by recognizing that y = ln(x^4/2) can be rewritten using logarithmic properties as y = ln(x^4) - ln(2), which simplifies to 4ln(x) - ln(2). The derivative is then found by differentiating each term separately, resulting in 4/x.
What is the significance of the derivative of the function representing the time to warm a frozen package of smoked salmon?
-The derivative of the function representing the time to warm a frozen package of smoked salmon (t') gives the rate of change of temperature per minute at any given time, which is useful for determining how quickly the salmon is warming at different stages.
How does the script demonstrate the use of exponential and logarithmic properties in calculus?
-The script demonstrates the use of exponential and logarithmic properties in calculus by simplifying expressions like ln(6x) into ln(6) + ln(x) and using properties such as ln(a^b) = b * ln(a) to rewrite and differentiate complex logarithmic expressions more easily.
Outlines
📚 Introduction to Derivatives of Logarithms
The video begins with an introduction to derivatives of logarithms, specifically focusing on the natural logarithm (ln). The presenter explains that the derivative of ln(x) with respect to x is 1/x, and while a proof is available in the book, it is not covered in the video. The importance of the chain rule is emphasized, and an example is provided to demonstrate its application in finding the derivative of ln(x^2 + 1), resulting in (2x)/(x^2 + 1).
🔢 Derivatives of Logarithms with Constant Multiples
The presenter continues with examples of derivatives involving logarithms with constant multiples. For instance, the derivative of -8 ln(x) is shown to be -8/x, maintaining the constant multiple through the differentiation process. The concept of the argument of a logarithm is introduced, and the derivative of ln(6x) is calculated, demonstrating the use of properties of logarithms and the chain rule, resulting in 1/x after simplification.
📈 Product and Quotient Rule Applications
The video covers the application of the product rule and quotient rule in the context of logarithmic functions. The presenter differentiates x^4 * ln(x) using the product rule, resulting in 3x^3 + x * ln(x). A similar approach is used for the quotient rule with ln(x)/x^4, leading to a derivative of (1 - 4ln(x))/x^5. The discussion highlights the importance of recognizing and applying these differentiation rules in various scenarios.
🎓 Logarithmic Properties and Derivatives
The presenter explores logarithmic properties, such as the ability to bring powers down in front of the logarithm, and uses these properties to simplify derivatives. An example given is the derivative of ln((x^4)/2), which is simplified to 4/x after applying logarithmic properties and the chain rule. The video emphasizes the utility of logarithmic properties in simplifying calculus problems and obtaining the correct derivatives.
📈 Advertising and Consumer Response Model
The video shifts to an application problem involving advertising and consumer response. A model n(a) is given, representing the number of units sold in relation to the amount spent on advertising (a). The presenter calculates the number of units sold when $1,000 is spent on advertising and finds the derivative n'(a) to understand the rate of change in units sold with respect to advertising spend. The concept of diminishing returns in advertising is introduced through the derivative n'(10), which is 20 units per thousand dollars of advertising.
🔢 Calculating Advertising Spend for Desired Sales
The presenter solves for the amount of advertising spend needed to achieve a sale of 1500 units, using algebraic manipulation of the given model. By setting n(a) to 1500 and solving for a, the presenter finds that approximately $12,000 needs to be spent on advertising to reach the sales target. This section demonstrates the practical use of derivatives in solving real-world problems related to business and marketing.
📉 Limit of Advertising Efficiency
The presenter discusses the limit of the derivative n'(a) as a approaches infinity, to determine the efficiency of spending more on advertising. It is shown that as the advertising spend increases, the additional units sold decrease, leading to a limit of zero for n'(a). This suggests that there comes a point where increasing the advertising budget does not yield a significant increase in sales, illustrating the concept of diminishing returns in advertising.
🍣 Thawing Time for Smoked Salmon
The video concludes with a problem involving the thawing time for a frozen package of smoked salmon. The presenter calculates the time needed to warm the package to 60 degrees Fahrenheit and the rate of temperature change per minute (t'(60)). The problem highlights the use of derivatives in understanding rates of change in real-world scenarios, such as the thawing process.
🕒 Time and Temperature Relationship
The presenter finds the derivative of the given thawing time function, which represents the rate of temperature change with respect to time. The derivative t' is calculated, and the presenter emphasizes the importance of units in understanding the meaning of the derivative. The video demonstrates the application of derivatives in physical scenarios, such as calculating the time it takes for a temperature change to occur.
🧮 Final Thoughts on Derivatives of Logarithms
The video ends with a recap of the key takeaways. The presenter reiterates the formula for the derivative of ln(x), which is 1/x, and the application of the chain rule when dealing with more complex logarithmic expressions. The importance of understanding and practicing these concepts is emphasized, and the presenter offers to answer questions in a live session.
Mindmap
Keywords
💡Derivatives
💡Natural Logarithm (ln)
💡Chain Rule
💡Proof
💡Newton's Notation
💡Constant Multiple
💡Product Rule
💡Quotient Rule
💡Logarithmic Properties
💡Applications of Derivatives
💡Limit
Highlights
The derivative of the natural logarithm function ln(x) with respect to x is 1/x.
A simple proof for the derivative of ln(x) is provided in the book but not covered in the brief calculus course.
The importance of remembering the chain rule when differentiating more complex logarithmic expressions.
Using Newton's notation, if f(x) = ln(x), then f'(x) = 1/x.
The derivative of ln(x^2 + 1) involves applying the chain rule, resulting in (1/(x^2 + 1)) * 2x.
Differentiating y = -8ln(x) shows the use of constant multiples in derivatives, yielding -8/x.
For f(x) = ln(6x), properties of logarithms allow the expression to be simplified to ln(6) + ln(x) before differentiation.
The product rule is applied when differentiating y = x^4 * ln(x), resulting in a derivative involving x^3 and ln(x).
The quotient rule is used to differentiate ln(x) / x^4, resulting in a derivative that simplifies to (1 - 4ln(x)) / x^5.
An application problem involves calculating the response to advertising, where n(a) represents the number of units sold based on advertising spend.
The limit of n'(a) as a approaches infinity is zero, indicating diminishing returns on advertising spend.
An example problem involves finding the time needed to warm a frozen package of smoked salmon to a certain temperature.
The derivative t'(60) represents the rate of temperature change per minute at 60 degrees Fahrenheit for the salmon package.
A mistake in the calculation of the temperature after eight hours is corrected by converting hours to minutes and recalculating.
The final temperature after eight hours is determined to be 70.4 degrees Fahrenheit, assuming the room temperature is 76 degrees and the initial temperature is 38 degrees.
The key takeaway is the derivative of ln(x) is 1/x, with the chain rule applied for more complex functions.
The chain rule for the derivative of ln(f(x)) is expressed as (1/f(x)) * f'(x), emphasizing the importance of understanding the rule rather than just memorizing it.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: