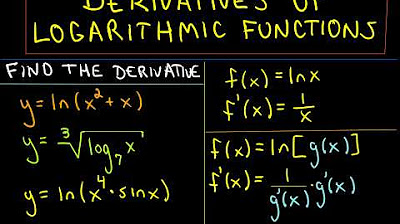Derivatives of Log Functions
TLDRThe video script is an educational lesson on the derivatives of logarithmic functions. It begins by establishing the relationship between logarithms and exponential functions, illustrating how a logarithm is essentially an exponent. The instructor then demonstrates how to convert between exponential and logarithmic forms with concrete examples, such as \(3^2 = 9\) being equivalent to \(\log_3(9) = 2\). The focus shifts to differentiating logarithmic functions by first rewriting them in exponential form, which allows for the application of known derivative rules. The script derives the general rule for the derivative of a logarithmic function, \( f'(x) = \frac{1}{x \ln(a)} \), where \( f(x) = \log_a(x) \), and extends this to the natural logarithm, \( (\ln(x))' = \frac{1}{x} \). The lesson further explores the derivatives of logarithmic functions combined with constants, products, quotients, and when the argument of the logarithm is a more complex expression, applying the chain rule as necessary. The instructor emphasizes the importance of simplification and provides a secondary definition for the derivative of the logarithm of absolute value of \( x \), which simplifies the derivative to \( \frac{1}{x} \) regardless of \( x \) being positive or negative. The script concludes with an invitation for students to ask questions and a prompt for further learning.
Takeaways
- 📚 The derivative of a logarithmic function ( f(x) = log_a(x) ) is ( 1/x ln(a) ), where ( ln(a) ) is the natural logarithm of the base ( a ).
- 🔗 Logarithms and exponential functions are connected; ( a^x = y ) is equivalent to ( log_a(y) = x ), which helps in differentiating logarithmic functions.
- ✅ The natural logarithm ( ln ) is a special case where the base is ( e ), and its derivative is ( 1/x ).
- 📈 When differentiating a logarithmic function, rewrite it in exponential form if necessary, and then apply the rules of differentiation.
- 📌 The derivative of a logarithmic function with a constant multiple can be found using the constant multiple rule, which states that the derivative of ( c * f(x) ) is ( c * f'(x) ).
- 🤔 For more complex logarithmic expressions, use the chain rule to differentiate the inner function and multiply by the derivative of the outer function.
- 🛠️ The quotient rule is applied when differentiating a logarithmic function in the numerator of a fraction, resulting in ( F'(x)G(x) - F(x)G'(x) )/(G(x)^2 ).
- 📉 When a logarithmic function includes an absolute value, the derivative remains ( 1/x ), as the absolute value does not affect the derivative of the logarithm.
- 🔧 Simplification of derivatives is often possible and recommended for cleaner expressions, but do not over-simplify to the point of obscuring clarity.
- 📝 Memorizing the derivative rules for logarithmic functions allows for quicker and more accurate differentiation in calculus problems.
- ➗ The derivative of a logarithmic function with a variable in the argument (other than ( x ) ) requires the use of the chain rule, multiplying by the derivative of the argument.
Q & A
What is the relationship between logarithms and exponential functions?
-Logarithms and exponential functions are inversely related. An exponential function in the form of 'a' raised to the power of 'x' equals 'y' can be rewritten as a logarithmic form, log base 'a' of 'y' equals 'x'. This shows that the base of the exponential function is the same as the base of the logarithm, and the exponent 'x' is the answer to the logarithm.
What is the derivative of f(x) = log base a of x?
-The derivative of f(x) = log base a of x is given by f'(x) = 1 / (x * ln(a)), where 'ln' represents the natural logarithm.
How do you differentiate a natural logarithm function?
-The derivative of a natural logarithm function, f(x) = ln(x), is f'(x) = 1 / x.
What is the derivative of a logarithmic function multiplied by a constant?
-The derivative of a logarithmic function multiplied by a constant, say c * log base a of x, is obtained by applying the constant multiple rule, resulting in c * (1 / (x * ln(a))).
What is the derivative of a logarithmic function when the argument is not x but another function, say u(x)?
-The derivative of a logarithmic function with an argument that is another function, f(x) = log base a of u(x), involves the chain rule and is given by f'(x) = (1 / (u(x) * ln(a))) * u'(x).
How do you rewrite a logarithmic function with a negative argument to simplify the derivative?
-You can use the absolute value to rewrite the logarithmic function, such as log base a of |x| or ln|x|, to simplify the derivative, which remains 1 / x regardless of whether x is positive or negative.
What is the common logarithm and how is its base implied?
-The common logarithm is a logarithm with the base of 10. When the base is not written explicitly, it is implied to be base 10, often referred to as 'log' without the base.
How does the derivative of an exponential function help in finding the derivative of a logarithmic function?
-Since logarithms and exponentials are inverse functions, differentiating an exponential function provides the derivative formula for the corresponding logarithmic function. For example, the derivative of a to the power of x is ln(a) * a to the power of x, which helps in finding the derivative of the logarithmic function as the reciprocal of this.
What is the product rule for derivatives and how is it applied when differentiating a function that is a product of two other functions?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function, i.e., (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x). It is applied by differentiating each function separately and then combining them according to the rule.
What is the quotient rule for derivatives and how is it used when differentiating a function that is a quotient of two other functions?
-The quotient rule states that the derivative of a quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator, i.e., [f(x) / g(x)]' = [g(x) * f'(x) - f(x) * g'(x)] / [g(x)^2]. It is used to find the derivative of a function that is one function divided by another.
Why is it important to keep natural logarithms in parentheses to avoid incorrect mathematical simplifications?
-Natural logarithms are represented as ln(x) and keeping them in parentheses helps to avoid the temptation of incorrectly simplifying expressions by treating the natural logarithm as a variable that can be reduced. The natural logarithm represents a decimal value and does not simplify in the same way as algebraic variables.
Outlines
📚 Introduction to Derivatives of Logarithmic Functions
The video begins with an introduction to the derivatives of logarithmic functions. It emphasizes the relationship between logarithms and exponential functions, explaining how a logarithm is essentially an exponent. The host provides the formula for converting between exponential and logarithmic forms, highlighting that the base of the exponential function and the base of the logarithm must be the same. The video also covers the natural logarithm, which has an implied base of 'e'. Several examples are given to illustrate the concept, such as converting exponential expressions to logarithmic form and vice versa. The importance of understanding both forms is stressed, as each can be more useful in different mathematical contexts.
🧮 Derivative Rules for Logarithmic Functions
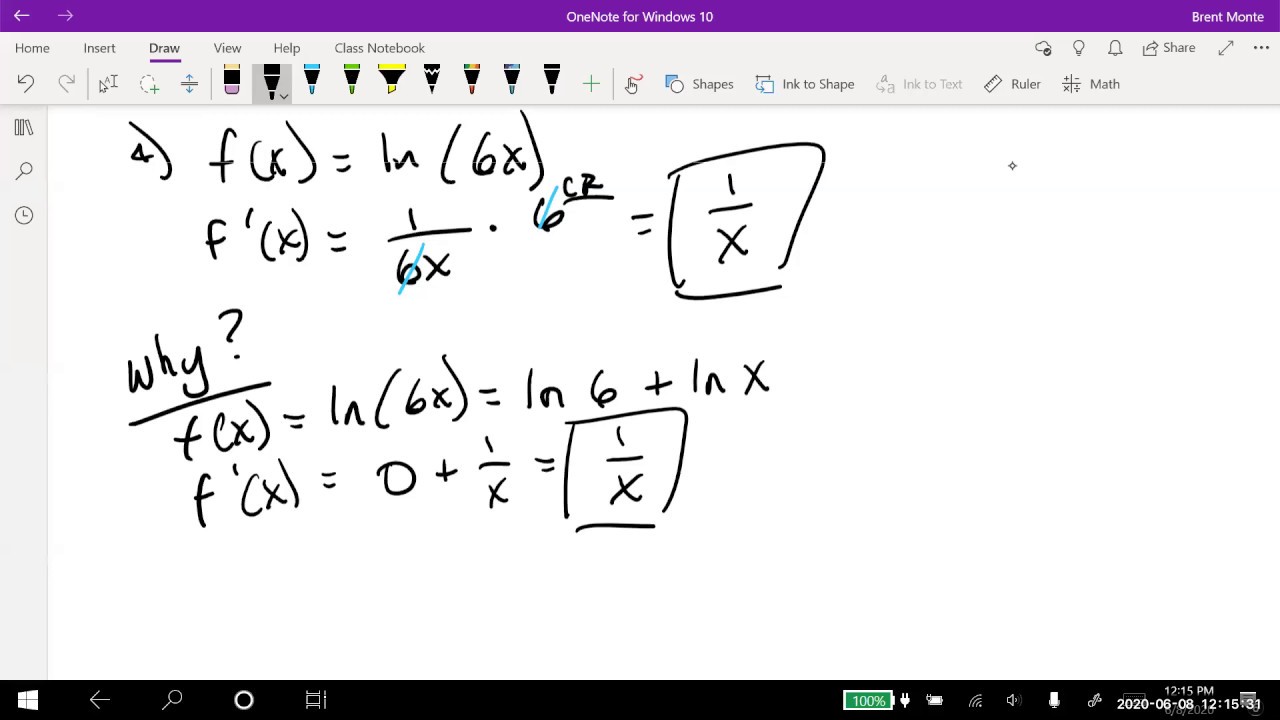
The host moves on to discuss the derivative rules for logarithmic functions. By converting a logarithmic function into its exponential form, the derivative can be found using known derivative rules for exponential functions. The formula for the derivative of a logarithmic function is derived, which involves the natural logarithm of the base and the derivative of the argument of the logarithm. The video also covers the derivative of the natural logarithm function, which simplifies to 1 over the argument. The host then generalizes these rules using the chain rule for more complex logarithmic expressions.
🔢 Derivatives of Logarithmic Functions with Constants
This section deals with the derivatives of logarithmic functions that are multiplied by constants. The constant multiple rule is applied to show that the derivative of a constant times a logarithmic function is simply the constant times the derivative of the logarithmic function. Examples are provided to illustrate this, including the derivative of a logarithmic function with a base of 4 and the common logarithm (base 10). The process of simplifying the derivative expressions is also demonstrated, emphasizing the importance of reducing fractions to their simplest form.
📈 Application of Chain Rule to Logarithmic Functions
The video continues with the application of the chain rule to logarithmic functions. It is shown that when the argument of the logarithm is not a simple x but a more complex expression, the chain rule must be used. The host walks through the process of differentiating a natural logarithm where the argument is a square root, demonstrating the use of the chain rule and simplification of the resulting expression. The emphasis is on correctly applying the chain rule and simplifying the derivative as much as possible without overcomplicating the final answer.
🤔 Product and Quotient Rule for Logarithmic Functions
The host explores the use of the product and quotient rules in the context of logarithmic functions. The product rule is applied to a function that is the product of a logarithmic function and a linear function. The quotient rule is then demonstrated on a function that is a logarithmic function divided by a linear function. The video shows how to find the derivatives in these cases, including the steps to simplify the expressions. The importance of recognizing common factors and simplifying the derivative expressions is highlighted.
🔁 Derivatives of Absolute Value Logarithmic Functions
The final section addresses the derivatives of logarithmic functions with absolute values. The host explains that the derivative of the logarithm of x and the logarithm of negative x are the same, leading to a unified rule using the absolute value. The video concludes with a reminder that the absolute value does not affect the derivative of logarithmic functions, whether the argument is positive or negative. The host encourages students to be comfortable with these concepts and offers help for any questions, signing off until the next lesson.
Mindmap
Keywords
💡Derivatives
💡Logarithms
💡Exponential Functions
💡Natural Logarithm
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Common Logarithm
💡Absolute Value
💡Differentiation
💡Logarithmic Identity
Highlights
Derivatives of logarithmic functions can be easily calculated using the connection between logarithms and exponential functions.
A logarithm is the inverse operation to exponentiation, where the exponent is represented by the logarithm.
The natural logarithm (base e) is a special case where the base is always e and is often denoted without the base.
Derivatives of exponential functions can be used to find derivatives of logarithmic functions by converting them into exponential form.
The derivative of a logarithmic function f(x) = log_a(x) is given by f'(x) = 1/(x * ln(a)) where ln(a) is the natural logarithm of the base.
For the natural logarithm, f(x) = ln(x), the derivative is f'(x) = 1/x.
The chain rule can be applied to generalize the derivative of a logarithmic function when the argument is not simply x.
If a logarithmic function is multiplied by a constant, the derivative is the constant times the derivative of the logarithmic function alone.
Product, quotient, and chain rules can be used in combination to find derivatives of more complex functions involving logarithms.
The derivative of a logarithmic function with a variable base remains 1/x * ln(base), regardless of the base.
When differentiating logarithms of negative values, the absolute value can be used to consolidate the derivative rule as it yields the same result for both positive and negative values.
The derivative of log_a(|x|) is 1/x * ln(a), which applies to both positive and negative values of x.
The derivative of ln(|x|) is 1/x, which is consistent regardless of x being positive or negative.
Concrete examples are provided to illustrate the conversion between exponential and logarithmic forms.
The derivative of a logarithmic function can be simplified by recognizing common factors and reducing fractions.
The process of differentiating logarithmic functions involves understanding and applying the relationship between the derivative of the exponential function and its logarithmic counterpart.
The use of the natural logarithm is emphasized in the context of differentiation, given its base e, which is a standard mathematical constant.
The importance of keeping natural logarithms in parentheses to avoid incorrect mathematical simplifications is highlighted.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: