BusCalc 14 Derivatives of Exponents
TLDRThe video script offers an in-depth exploration of derivatives, specifically focusing on exponential functions. It begins by emphasizing the importance of understanding derivatives as the slope of the tangent line to a curve at any given point. The distinction between power functions, where the variable is the base and the exponent is constant, and exponential functions, where the base is constant and the exponent is the variable, is clearly outlined. The presenter highlights two unique functions: y = 1/2x^2, whose derivative equals the input value, and y = e^x, whose derivative equals the output value. The script then delves into the derivatives of exponential functions with different bases, illustrating that they are proportional to the output value, with the constant of proportionality being the natural logarithm of the base. Several examples are provided to demonstrate the application of the product, quotient, and chain rules in finding derivatives, encouraging viewers to pause and attempt the practice problems before revealing the solutions. The video concludes with a reminder of the importance of practice and struggle in mastering mathematical concepts.
Takeaways
- 📌 The derivative of a function represents the slope of the tangent line at any point on the curve of the function.
- 📝 It's crucial to distinguish between power functions (e.g., x^7) and exponential functions (e.g., 7^x), where the base and exponent roles are reversed.
- 🔑 A unique property of the function y = (1/2)x^2 is that its derivative is equal to the input (x), making the slope of the tangent line at any point the same as the x-value.
- 🧮 The function y = e^x has a special derivative in that it equals the output of the function itself, which is a distinctive property not shared by exponential functions with other bases.
- 📈 For exponential functions with bases other than e, the derivative is proportional to the output, with the constant of proportionality being the natural logarithm of the base.
- 💡 The derivative of e^x simplifies to e^x because the natural logarithm of e is 1, maintaining consistency in the derivative rules for exponential functions.
- 📚 Memorize the derivative formulas for exponential functions, especially for the base e, which is a fundamental concept in calculus.
- 🔧 Apply the product rule (f'g + fg') when differentiating the product of two functions, and the quotient rule (f'g - fg')/g^2 when differentiating a quotient of two functions.
- 🎓 Practice is essential for mastering derivative calculations, including those involving exponential functions, and should involve attempting problems independently before reviewing solutions.
- 🔗 The chain rule is applicable when differentiating composite functions, expressed as dy/du * du/dx, where u is an intermediate variable that simplifies the expression.
- 📉 When dealing with roots or fractional exponents, they can be rewritten as powers to simplify the derivative, such as the square root of a quantity being equivalent to that quantity to the power of 1/2.
Q & A
What is the derivative of the exponential function e^x?
-The derivative of the exponential function e^x is also e^x. This is due to the special property of the exponential function with base e, where the derivative is equal to the function itself.
How does the slope of the tangent line to a function relate to the derivative?
-The derivative of a function at a given point represents the slope of the tangent line to the function at that point. It gives the rate of change of the function's output with respect to a change in the input.
What is the difference between a power function and an exponential function?
-A power function has the form x^n, where x is the independent variable and n is a constant exponent. An exponential function, on the other hand, has the form a^x, where a is a constant base and x is the exponent. The key difference is that in a power function, the variable is the base, while in an exponential function, the variable is the exponent.
What is the derivative of the function y = (1/2)x^2?
-The derivative of the function y = (1/2)x^2 with respect to x is simply x. This is because the power rule brings down the exponent and reduces it by 1, resulting in x^(2-1) = x^1, which simplifies to x.
What is the property that makes the function y = e^x unique?
-The function y = e^x is unique because its derivative is equal to the function itself. This means that the slope of the tangent line to the curve of the function at any point is equal to the output value of the function at that point.
How does the derivative of an exponential function with a base other than e compare to the derivative of e^x?
-The derivative of an exponential function with a base other than e is proportional to the function's output. Specifically, the derivative of a^x is ln(a) * a^x, where ln(a) is the natural logarithm of the base a. This is different from e^x, whose derivative is exactly equal to itself, not just proportional.
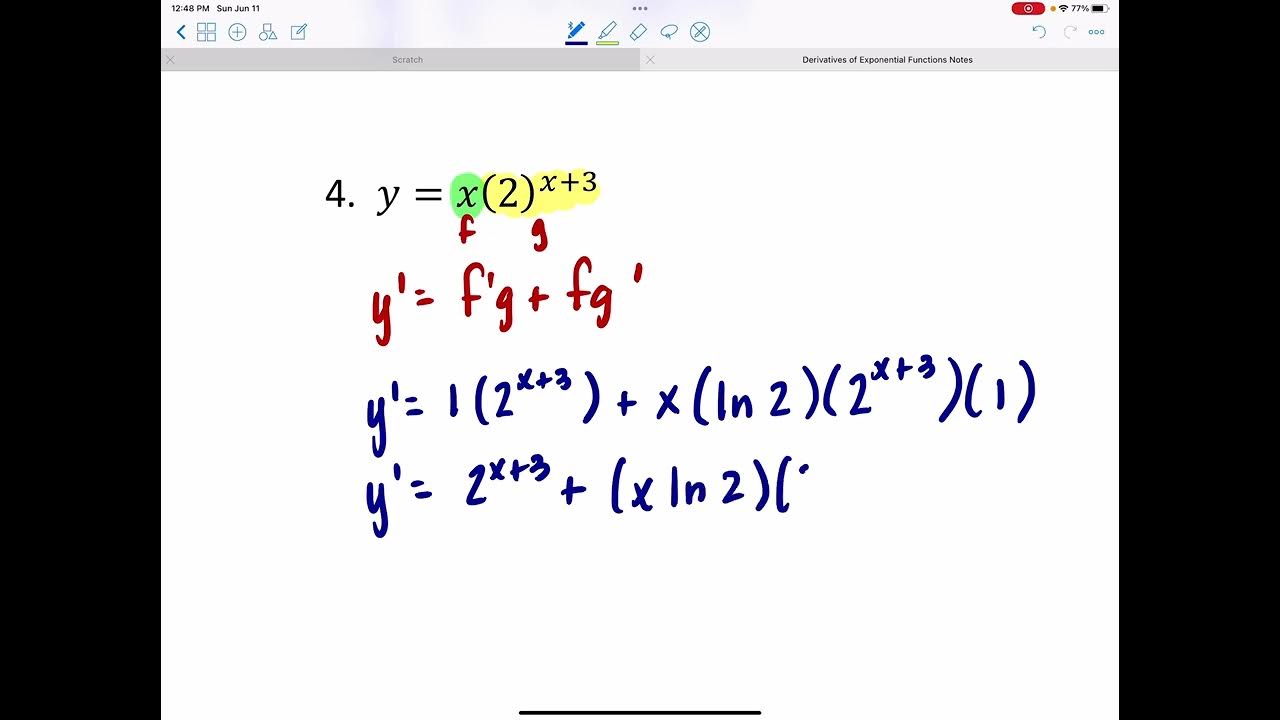
What is the product rule for derivatives, and how is it applied?
-The product rule states that the derivative of a product of two functions, f(x) and g(x), is given by (f'(x) * g(x)) + (f(x) * g'(x)), where f'(x) and g'(x) are the derivatives of f and g, respectively. It is applied when finding the derivative of a function that is the product of two other functions.
What is the quotient rule for derivatives, and how is it used?
-The quotient rule states that the derivative of a quotient of two functions, f(x)/g(x), is given by (f'(x) * g(x) - f(x) * g'(x)) / (g(x))^2. It is used when finding the derivative of a function that is the quotient of two other functions.
What is the chain rule for derivatives, and how does it simplify the process of finding derivatives of composite functions?
-The chain rule states that the derivative of a composite function, say y = f(u(x)), is given by (dy/du) * (du/dx), where u is an intermediate function of x. It simplifies the process by allowing us to break down the composite function into simpler parts, find the derivative of the outer function with respect to the inner function, and then multiply by the derivative of the inner function with respect to the original variable.
How does the concept of simplifying derivatives apply to the given examples in the script?
-Simplifying derivatives involves collecting like terms, factoring, and canceling common factors to express the derivative in its simplest form. In the examples provided, the presenter simplifies the derivatives of various functions by applying algebraic rules and properties, making the expressions easier to understand and work with.
What is the importance of practicing derivative problems, and how does it contribute to mastering the concept?
-Practicing derivative problems is crucial for solidifying understanding and improving problem-solving skills. By working through a variety of problems, students can apply the rules of differentiation in different contexts, recognize patterns, and gain a deeper understanding of the underlying concepts. It also helps in developing the ability to manipulate algebraic expressions and apply the product, quotient, and chain rules effectively.
Outlines
📚 Introduction to Exponential Functions and Derivatives
The video begins with an introduction to the topic of derivatives of exponential functions. It emphasizes the importance of understanding the derivative as the slope of the tangent line to a curve at any given point. The distinction between power functions, where the variable is the base and the exponent is constant, and exponential functions, where the base is constant and the variable is the exponent, is clarified. Two special functions are highlighted: y = (1/2)x^2, whose derivative equals the input x, and y = e^x, where the derivative equals the output of the function itself.
🔢 Derivatives of Exponential Functions with Different Bases
The video explains the derivatives of exponential functions with bases other than e. It is shown that the derivative of e^x is simply e^x, while for other bases like 2^x, the derivative is the natural logarithm of the base times the function itself. This pattern holds for any base 'a', with the derivative being the natural logarithm of the base times a^x. The video also clarifies that the derivative of e^x can be seen as consistent with this rule, given that the natural logarithm of e is 1.
📈 Applying the Product Rule to Exponential Functions
The presenter demonstrates the use of the product rule for derivatives, which is applied when differentiating the product of two functions. An example is given where the derivative of 2^x * x^2 + 1 is calculated. The process involves identifying the two functions being multiplied (f and g), finding their respective derivatives (f' and g'), and then applying the product rule formula: f'g + fg'.
📉 Using the Quotient Rule for Exponential Functions
The quotient rule for derivatives is introduced, which is necessary when differentiating a quotient of two functions. An example is shown where the derivative of e^t / t^2 is calculated. The process involves applying the quotient rule formula: (f'g - fg') / g^2, where f is the numerator and g is the denominator of the original function. The video also provides a cleaned-up version of the derivative for better understanding.
🔁 Derivative Chain Rule for Composite Exponential Functions
The video covers the derivative chain rule, which is used for composite functions. An example is given where the derivative of y = e^(x^2) is calculated. The chain rule is applied by introducing an intermediate variable u = x^2, which simplifies the differentiation process. The derivative dy/du is found first, followed by the derivative du/dx, and these are then multiplied to find the overall derivative dy/dx.
🔍 Simplifying Exponential Derivatives with Chain Rule
The video concludes with a discussion on simplifying derivatives of exponential functions using the chain rule, particularly when dealing with exponents that are powers themselves. An example is given where the derivative of √(10^t) is simplified by recognizing that √(x^n) is equivalent to x^(n/2), and consecutive exponents can be combined by multiplication. The video encourages practice and emphasizes the importance of struggling through problems as a part of the learning process.
Mindmap
Keywords
💡Derivative
💡Exponential Function
💡Power Function
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Natural Logarithm
💡Slope of the Tangent Line
💡Constant of Proportionality
💡Composite Function
💡Differentiation Rules
Highlights
Derivative is defined as the slope of the tangent line to a curve at a given point.
Differentiating between power functions (e.g., x^7) and exponential functions (e.g., 7^x) is crucial.
The function y = (1/2)x^2 has a unique property where its derivative is equal to the input x.
The function y = e^x is special because its derivative is equal to the output of the function itself.
For exponential functions with bases other than e, the derivative is proportional to the output, with a constant multiplier of the natural log of the base.
The derivative of e^x simplifies to e^x because the natural log of e is 1.
Product rule for derivatives is f'g + fg', where f and g are functions.
Quotient rule for derivatives is (f'g - fg') / g^2, applicable when differentiating a quotient of two functions.
Chain rule for derivatives allows for the differentiation of composite functions by breaking them down into simpler components.
The derivative of a function y = e^(x^2) is found using the chain rule, resulting in e^(x^2) * 2x.
When dealing with exponents, consecutive exponents can be simplified by multiplying them, e.g., (x^3)^2 becomes x^6.
The derivative of a function involving square roots can be simplified by expressing the square root as a half power.
Practice problems are essential for mastering derivative concepts and should be attempted before viewing solutions.
The process of differentiating functions using product, quotient, and chain rules is demonstrated through multiple examples.
The importance of simplifying derivatives after applying differentiation rules for clarity and understanding is emphasized.
The video concludes with encouragement to practice and struggle through problems to improve mathematical skills.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: