BusCalc 15 Derivatives of Logarithms
TLDRThis educational video script delves into the intricacies of derivatives, specifically focusing on logarithmic functions. The presenter begins by revisiting the power rule for derivatives and introduces the concept of the anti-derivative, which is essentially the reverse process of differentiation. The script then explores the anti-derivatives of various powers of x, leading to the revelation that the antiderivative of x to the power of negative one is the natural logarithm of x. The video emphasizes the importance of understanding the underlying logic behind mathematical rules rather than just memorizing them. It proceeds to illustrate the application of the product, quotient, and chain rules in calculating derivatives, using logarithmic functions as examples. The presenter encourages students to practice these concepts to solidify their understanding, providing multiple examples and inviting viewers to pause and attempt their own solutions before revealing the answers. The script concludes with an emphasis on the value of practice in mastering mathematical concepts.
Takeaways
- 📚 The power rule is a fundamental principle in calculus for differentiating functions of the form x^n, where n is a constant.
- 🧠 The brain teaser in the video encourages students to actively think about the power rule and its application to various exponents, including negative and zero powers.
- 🔑 The concept of the anti-derivative is introduced as the opposite process of taking a derivative, symbolized by the ∫ sign, which is a tall 'S'.
- 🤔 The video poses a challenge to find the anti-derivative of x^(-3), which leads to a discussion on how to manipulate functions to achieve the desired derivative.
- 📉 The pattern of the power rule is emphasized, showing how the exponent changes when taking the derivative, and how this pattern is broken when dealing with the natural logarithm function.
- 📌 Memorization is stressed for understanding the derivative of the natural log function, which is 1/x, and the relationship between negative exponents and their derivatives.
- 📐 The video explains the derivative of the natural log function using the properties of exponential and logarithmic functions, highlighting the inverse nature of these functions.
- 📝 The importance of practicing math problems is emphasized, with the video providing several examples and encouraging students to pause and attempt their own solutions.
- 🔍 The product rule, quotient rule, and chain rule are all demonstrated through examples, showing how they are applied to functions involving logarithms.
- 📐 The chain rule is particularly highlighted in the context of more complex functions, such as the square root of a logarithm, to show how to break down the problem into simpler components.
- 📈 The video concludes by encouraging further practice with logarithmic derivatives, emphasizing that practice is key to mastering mathematical concepts.
Q & A
What is the power rule for derivatives?
-The power rule states that the derivative of x raised to the power of n, where n is a constant, is n times x to the power of n minus one (d/dx [x^n] = n * x^(n-1)).
What is the derivative of x to the power of zero?
-The derivative of x to the power of zero is 0, because x^0 is equal to 1, and the derivative of a constant is zero.
What is the anti-derivative and how is it denoted?
-An anti-derivative is a function whose derivative is a given function. It is denoted by a tall, elongated 'S' symbol, often referred to as an 'S' with a bar through it, and is read as 'the integral of'.
What is the relationship between the derivative and the anti-derivative of a function?
-The derivative and the anti-derivative are inverse operations. The derivative of an anti-derivative of a function will return the original function, and vice versa.
What is the antiderivative of x to the negative three power?
-The antiderivative of x to the negative three power is negative one half x to the negative two power.
What is the antiderivative of x to the negative one power?
-The antiderivative of x to the negative one power is the natural log of the absolute value of x (ln|x|).
What is the derivative of the natural log function with respect to x?
-The derivative of the natural log function with respect to x is 1 over x (d/dx [ln(x)] = 1/x).
What is the natural logarithm (ln)?
-The natural logarithm is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718.
How is the derivative of the natural log function derived?
-The derivative of the natural log function is derived by setting y as the natural log of x, then using the property of inverse functions that e^(ln(x)) = x, and applying the chain rule to show that dy/dx = 1/x.
What is the product rule for derivatives?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function (d/dx [f(x) * g(x)] = f'(x) * g(x) + f(x) * g'(x)).
What is the quotient rule for derivatives?
-The quotient rule states that the derivative of a quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator (d/dx [f(x) / g(x)] = [g(x) * f'(x) - f(x) * g'(x)] / [g(x)^2]).
Outlines
📘 Introduction to Derivatives of Logarithmic Functions
The video begins by revisiting the power rule of derivatives, exemplified through various powers of x. It highlights the straightforward calculation of derivatives for powers ranging from positive to negative, setting the stage for more complex functions. The focus then shifts to introducing the concept of antiderivatives, using a clear step-by-step approach to explain how to reverse the process of differentiation. The instructor emphasizes understanding the power rule in this context before moving on to the concept of antiderivatives with a graphical representation (tall squiggle) and practical examples to illustrate the process.
🔍 Deep Dive into Antiderivatives
This segment elaborates on calculating antiderivatives, particularly for negative powers of x. The instructor meticulously explains the process of finding antiderivatives for x to the negative three and negative two powers, using algebraic manipulation to achieve the correct forms. This thorough explanation aims to cement the viewer's understanding of antiderivatives as essentially performing the inverse operation of derivatives. The discussion includes correcting a typo related to antiderivative prompts and rounds off with a conceptual analysis of the patterns observed when dealing with negative exponents.
🤔 The Unique Case of the Natural Logarithm
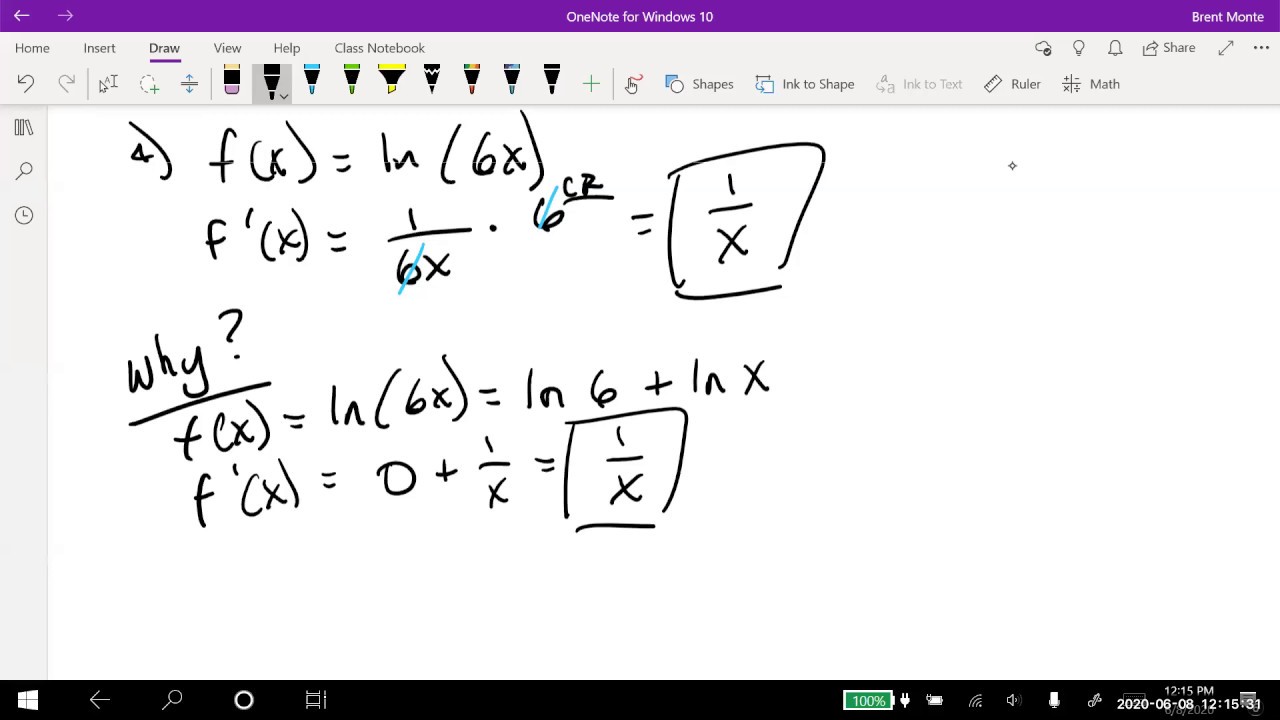
The discussion takes an intriguing turn as the instructor explains the antiderivative of x to the negative one power, revealing that unlike other integer powers, it does not yield a result involving x but rather involves the natural logarithm. This section focuses on the uniqueness of the natural log function as an antiderivative and the importance of memorizing its derivative, 1 over x. The instructor further expands on the relationships between various logarithmic functions, their derivatives, and the mathematical constants involved, particularly emphasizing the conceptual depth and interconnections within logarithmic functions.
🧠 Technical Explanation of Logarithmic Derivatives
This part of the video presents a technical explanation of how the derivative of the natural log function, represented as 1 over x, is derived using the chain rule. The instructor takes a step-by-step approach, using the relationship between e to the power x and the natural log to demonstrate this derivative visually and algebraically. The explanation is aimed at demystifying the derivation process and showing the logical foundation of this important mathematical rule. The instructor's passion for explaining the rationale behind mathematical rules is evident, as they encourage viewers to appreciate the logical reasoning in mathematics.
📐 Applying Logarithmic Derivatives in Practice
The video progresses to practical applications of logarithmic derivatives, incorporating rules like the product rule, quotient rule, and chain rule in various examples. Each example is structured to apply these rules to functions involving logarithms, with detailed steps and explanations provided. The instructor encourages viewers to practice these examples on their own, emphasizing the necessity of hands-on practice to master the concepts discussed. This segment is essential for viewers to understand how to manipulate and derive functions involving logarithms in different mathematical contexts.
🔎 Advanced Logarithmic Differentiation Techniques
The instructor discusses more complex scenarios involving logarithmic differentiation using the quotient rule. The segment includes step-by-step derivations where logarithms are either in the numerator or denominator, demonstrating the nuanced application of the quotient rule in these cases. The instructor aims to simplify these complex derivations, emphasizing understanding and application over rote memorization. Practical examples are provided to reinforce learning, and viewers are encouraged to pause the video and attempt these problems independently to test their understanding.
🚀 Conclusion and Encouragement for Independent Practice
In the concluding segment, the instructor wraps up the discussion on logarithmic derivatives and encourages viewers to engage with practice problems independently. They stress the importance of applying the learned concepts through practice to reinforce understanding and proficiency. The instructor provides final thoughts on the educational approach, emphasizing the importance of understanding the reasoning behind mathematical rules and not just memorizing them. The session ends with a call to action for viewers to continue practicing and improving their skills in calculus.
👋 Sign-Off from the Instructor
The instructor signs off, promising more in-depth discussions in future videos. This brief closing serves as an invitation for continued learning and engagement with upcoming content, reinforcing the educational journey viewers are on with this series.
Mindmap
Keywords
💡Derivatives
💡Logarithmic Functions
💡Power Rule
💡Anti-Derivative
💡Natural Logarithm
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Inverse Functions
💡Derivative of Constant
💡Logarithm Base
Highlights
Introduction of logarithmic function derivatives and a brain teaser to engage the audience.
Explanation of the power rule for derivatives, including examples with positive and negative exponents.
Derivation of the constant function x^0, emphasizing the concept that the derivative of a constant is zero.
Introduction of the anti-derivative concept, which is the opposite of taking the derivative.
Demonstration of finding the anti-derivative of x to the power of -3, leading to the discovery of a pattern.
Correction of a typo and continuation of the discussion on anti-derivatives of x to the power of -2 and -1.
Brain teaser: Encouraging the audience to think about the anti-derivative of x to the power of -1.
Revelation that the anti-derivative of x to the power of -1 is the natural logarithm of x (ln x).
Discussion on the uniqueness of the natural logarithm's derivative, which is 1/x, contrasting with the power rule pattern.
Explanation of the derivative of the natural log function using the properties of e^x and the chain rule.
Product rule application to a function involving a logarithm base 2 and a quadratic function.
Quotient rule application to a function with natural log t in the numerator and t squared in the denominator.
Chain rule application to find the derivative of the square root of the logarithm base 10 of t.
Emphasis on the importance of practicing derivative calculations for mastery.
Instruction to pause the video for practice problems, fostering an interactive learning experience.
Solution walkthrough for practice problems, reinforcing the learning process.
Final encouragement for further practice and a teaser for the next video's content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: