Rules for Integration
TLDRIn this educational video, Professor Money delves into the fundamental rules of integration, focusing on finding anti-derivatives. He explains that integration involves finding functions whose derivatives equal a given function, starting with the simple case of a constant function where the antiderivative is the constant times the variable plus a constant. The video then covers the power rule, which is the most frequently used, illustrating how to adjust the exponent and multiply by the reciprocal. Professor Money also discusses the integral of 1/x, which results in the natural logarithm of the absolute value of x, and the integral of exponential functions. Additionally, he introduces two key properties of integration: the ability to factor out constants and the ability to integrate functions separately and then combine them. The video concludes with examples that apply these rules and properties, emphasizing the importance of practice to master integration techniques.
Takeaways
- 📚 The integral symbol ∫ with dx represents finding the antiderivative of a function, which is a family of functions whose derivative is the integrand.
- 🔢 For a constant k, the antiderivative is kx + C, where C is an arbitrary constant, because the derivative of a constant is zero.
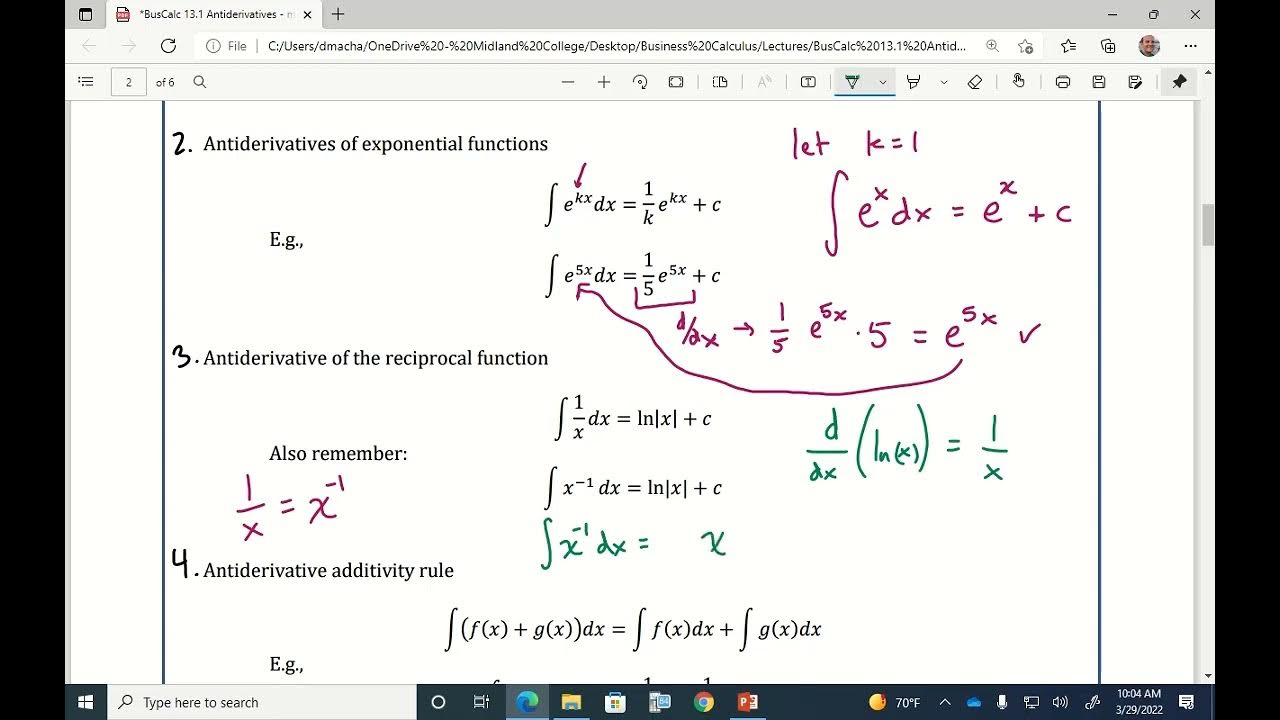
- ✋ The power rule for integration states that the antiderivative of x^n is (x^(n+1))/(n+1) + C, where n is not equal to -1.
- 📈 The natural logarithm function ln|x| is the antiderivative of 1/x, but only for x to the power of -1, due to the logarithmic property.
- 📈 For exponential functions, the antiderivative of e^(ax) is (1/a)e^(ax) + C, where a is a constant and the chain rule is reversed in integration.
- ➕ The integral of a sum of functions can be found by integrating each function separately and then adding or subtracting the results.
- ✖️ The integral of a constant times a function allows you to factor out the constant from the integral, simplifying the calculation.
- 🔁 The constant of integration, C, can be placed at the end of the integral expression after all terms have been integrated, as constants can be combined into a single constant term.
- 🔁 The antiderivative of a function can be checked by differentiating it and ensuring that it yields the original function.
- 🚫 The power rule does not apply to integrals of the form 1/x^n where n is not -1; instead, use the natural logarithm for n = -1.
- 📝 Practice is essential for mastering integration techniques, as it helps to improve speed and accuracy in solving integral calculus problems.
Q & A
What is the main goal of integration in calculus?
-The main goal of integration in calculus is to find anti-derivatives, which are the family of all functions whose derivative is the given function.
What is the integral of a constant with respect to x?
-The integral of a constant (k) with respect to x is k times x plus a constant (kx + C), because the derivative of a constant times x is the constant itself.
What is the power rule for integration?
-The power rule for integration states that the integral of x to the power of n with respect to x is (x to the power of n+1) divided by (n+1) plus a constant, written as (1/(n+1))x^(n+1) + C.
How do you integrate the function 1/x?
-The integral of 1/x is the natural logarithm of the absolute value of x plus a constant, written as ln|x| + C.
What is the rule for integrating an exponential function like e^(ax)?
-The integral of e^(ax) with respect to x is (1/a)e^(ax) plus a constant, because the derivative of e^(ax) is ae^(ax), and integration reverses the multiplication by 'a' to division by 'a'.
What is the first property of integration mentioned in the script?
-The first property of integration mentioned is that the integral of a constant times a function can be factored out as the constant times the integral of the function.
What is the second property of integration discussed in the script?
-The second property of integration discussed is that the integral of one function plus or minus another function can be broken up into separate integrals, similar to how addition and subtraction work in differentiation.
How do you integrate a function like 3x^2 + 4x - 7?
-You can integrate each term separately using the power rule for polynomials and then combine the results, factoring out constants where possible, and finally adding a constant of integration at the end.
What is the integral of 5/x + x^(-3) with respect to x?
-The integral can be broken into two parts: 5 times the natural logarithm of the absolute value of x plus (-1/2x^2) plus a constant, using the property and power rule for integration.
Why can't the power rule be used for integrating x^(-3)?
-The power rule is specifically for integrating x^(-n) where n is a positive integer. When n is not equal to 1, you cannot use the natural logarithm form, and you must use the power rule instead.
How does one check the correctness of an integration result?
-You can check the correctness of an integration result by differentiating the result and comparing it to the original function to be integrated.
Outlines
📚 Introduction to Integration Rules
Professor Money introduces the concept of integration as finding anti-derivatives. He explains that when integrating a constant 'k' with respect to 'x', the result is 'kx' plus a constant 'c'. This is because the derivative of a constant is zero, so it does not affect the result. The video also covers the power rule for integration, which involves increasing the exponent by one and multiplying by the reciprocal of the new exponent, followed by adding 'c'. An example given is integrating x to the ninth power, resulting in (1/10)x to the tenth plus 'c'. The power rule is emphasized as the most frequently used rule in integration.
🔢 Applying Integration Rules and Properties
The video continues with examples of applying the basic rules of integration. It demonstrates how to integrate more complex expressions, such as '3x^2 + 4x - 7', by breaking it down into simpler parts and applying the power rule. The constant multiple can be factored out, and each term is integrated separately. The result is 'x^3 + 2x^2 - 7x + c', which is confirmed by differentiating to get back the original expression. The video also covers the integration of rational functions and exponential functions, emphasizing the use of the natural logarithm for '1/x' and the handling of exponential functions with variable exponents. The properties of integration, which allow for the separation of integrals into sums and the factorization of constants, are also discussed.
🚫 Limitations of the Power Rule for Integration
The final part of the script addresses the limitations of the power rule for integration, particularly when dealing with '1/x'. It explains that the power rule cannot be applied to '1/x' by simply adding one to the exponent, as this would result in an undefined expression ('x^0' is not valid in this context). Instead, the natural logarithm is used for the integral of '1/x'. The video concludes with encouragement to practice the integration rules and properties, highlighting their importance in mastering calculus. It also includes a call to action for viewers to like, subscribe, and continue learning.
Mindmap
Keywords
💡Integration
💡Antiderivative
💡Constant
💡Power Rule
💡Natural Logarithm
💡Exponential Function
💡Chain Rule
💡Properties of Integrals
💡Derivative
💡Constant of Integration (C)
💡Differentiation
Highlights
Integration is the process of finding anti-derivatives, which are all functions whose derivative is a given function.
The integral of a constant (k) with respect to x is k times x plus a constant.
The power rule for integration states that the integral of x to the n power is (x to the n+1 power) divided by (n+1) plus a constant.
For the integral of 1 over x, the result is the natural logarithm of the absolute value of x plus a constant.
The derivative of e to the a x power is the entire exponential function e to the a x, but in integration, it's multiplied by the reciprocal of a.
Properties of integration allow for factoring out constants and breaking up integrals into sums or differences of integrals.
The integral of a sum or difference of functions can be found by integrating each function separately and then combining the results.
When integrating a polynomial, constants can be factored out, and the power rule can be applied to each term.
The integral of 3x squared plus 4x minus 7 with respect to x can be solved by integrating each term separately and then combining.
The derivative of the integrated function can be used to verify the result of an integration problem.
When integrating a function like 5 over x plus x to the negative 3, it can be broken into two separate integrals and solved individually.
The power rule cannot be applied to x to the zero power, which is why the natural logarithm is used for x to the negative one.
Negative exponents can be handled by adjusting the exponent and using the reciprocal in the integration process.
Practice is essential for mastering integration techniques and becoming more efficient in solving problems.
Remembering the four basic rules of integration and the two properties is key to solving a wide range of integration problems.
The video provides a comprehensive guide to the rules and properties of integration, with practical examples to illustrate the concepts.
Subscribing to the channel and liking the video can support the content creator and help others find this educational resource.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: