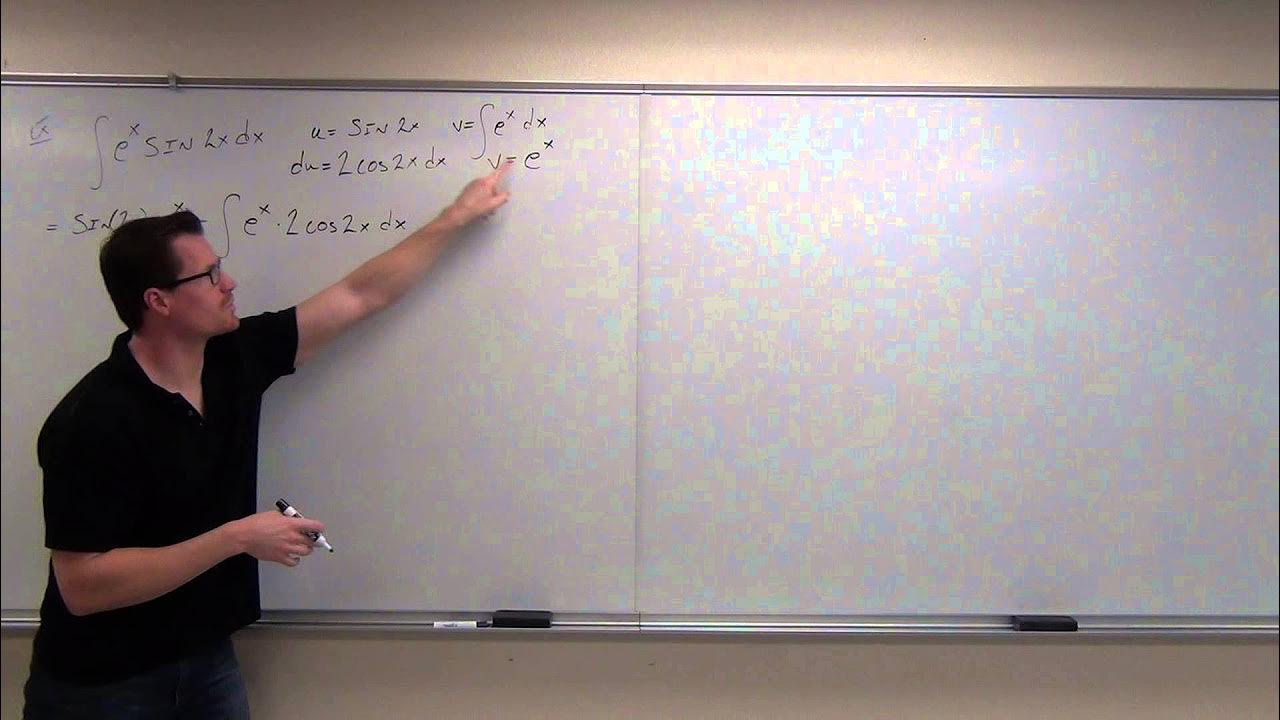Calculus AB Unit 6 Review
TLDRThis comprehensive video tutorial delves into the intricacies of basic integration techniques, guiding viewers through a variety of integral problems. The instructor begins by simplifying and integrating polynomial and rational functions, emphasizing the use of power rules and recognizing derivatives for easier integration. The video progresses to tackle trigonometric integrals, employing the technique of thinking in terms of derivatives to find antiderivatives. It also covers integrals involving products and quotients, where the instructor advises simplifying expressions before integrating. A unique approach to definite integrals of even and odd functions is presented, leveraging the functions' symmetry properties to simplify calculations. The video also explores the application of integrals in physics, including calculating average velocities and positions of moving particles, as well as total distances traveled. It concludes with a discussion on the meaning of integrals in context, such as the average value of a function over an interval and the use of Riemann sums for approximation. The tutorial is rich with examples, offering a clear understanding of integration concepts and their practical applications.
Takeaways
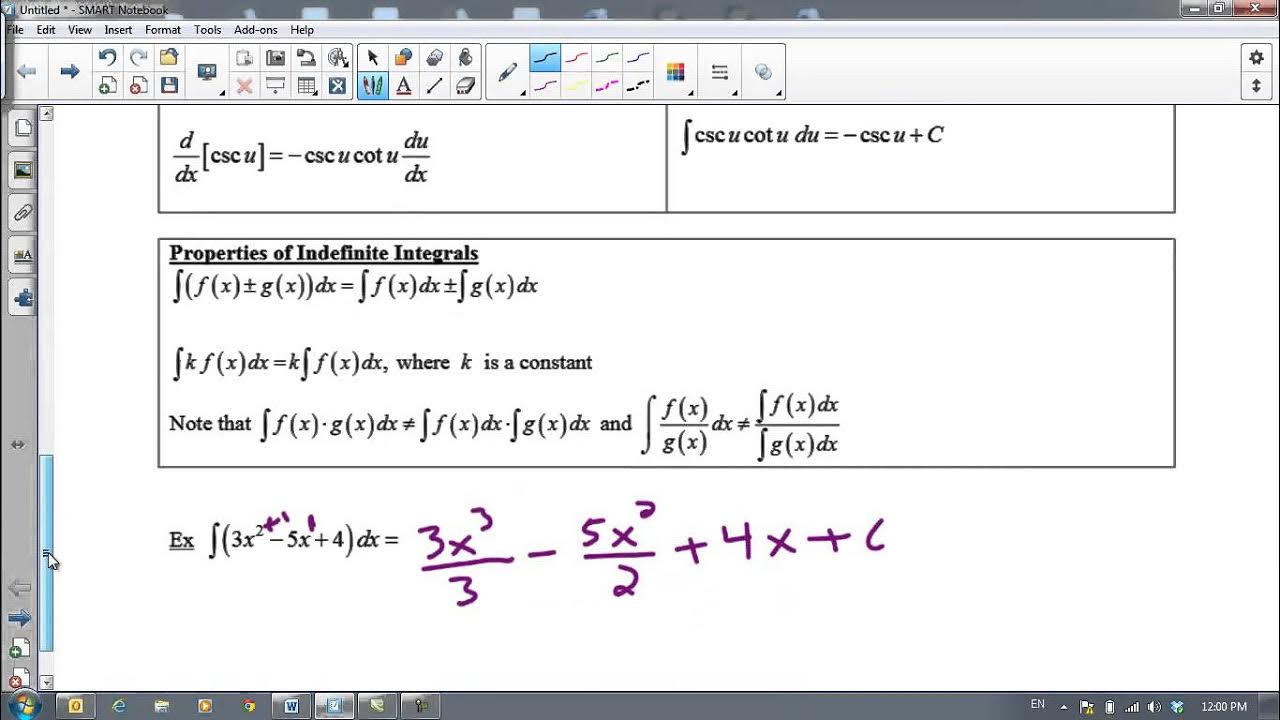
- 📚 Start by finding the antiderivative of each term in the integral separately, such as 3x for the constant 3, and using the power rule for terms like 2x.
- 🔑 Memorize common derivatives like 1/x, which is the integral of -1/x^2, to simplify integration problems.
- 🧮 When integrating by parts, think in terms of the derivative of what will produce what you're integrating, which helps in selecting u and dv.
- 🌟 For even and odd functions, leverage their properties: even functions are symmetric about the y-axis, and odd functions have an area of zero when integrated from a negative to a positive interval of the same length.
- ✅ Use properties of integrals to simplify expressions, such as factoring out constants and separating terms into individual integrals.
- 🏞️ When evaluating definite integrals, substitute the limits of integration into the antiderivative and simplify the result.
- 🔄 For problems involving rates of change, like snow accumulation or particle velocity, integrate the rate to find the total change over time.
- 🚗 To find average velocity or acceleration, use the average value of the velocity or acceleration function over the given interval.
- 📊 For estimating values from data, use the average rate of change over small intervals around the point of interest, or Riemann sums for approximations.
- 🧹 Simplify the integral before applying u-substitution to ensure that the substitution directly relates to the parts of the integral that can be easily integrated.
- 🔢 When performing u-substitution, always remember to substitute back (reverse substitute) to express the final answer in terms of the original variable.
Q & A
What is the antiderivative of 3 with respect to X?
-The antiderivative of a constant, such as 3, with respect to X is simply the constant multiplied by X, which in this case is 3X.
How do you find the antiderivative of 2x using the power rule?
-Using the power rule, which states that the antiderivative of x^n (where n is a constant) is x^(n+1)/(n+1), the antiderivative of 2x is 2x^2/2, which simplifies to x^2.
What is the antiderivative of 1/x?
-The antiderivative of 1/x is the natural logarithm of the absolute value of x, written as ln|x|, plus a constant C.
How can you integrate the function 4x * sqrt(x) with respect to X?
-First, simplify 4x * sqrt(x) to 4x * x^(1/2), which is 4x^(3/2). Then, apply the power rule to integrate x^(3/2) to get (4/5)x^(5/2) plus a constant C.
What is the integral of a function over a symmetric interval for an even function?
-For an even function, the integral over a symmetric interval [a, a] is equal to twice the integral from 0 to a of the function, since the function is symmetric about the y-axis.
What is the integral of an odd function over a symmetric interval?
-For an odd function, the integral over a symmetric interval [a, a] is always zero because the positive and negative areas under the curve cancel each other out.
How do you find the average velocity of a particle on a given interval?
-The average velocity is found by taking the antiderivative of the velocity function and then evaluating it at the endpoints of the interval and finding the difference, which gives the change in position over the change in time.
What is the average value of a function on a given interval?
-The average value of a function on an interval [a, b] is given by (1/(b-a)) * ∫[a, b] f(x) dx, which represents the average value of the function f over the interval.
How do you determine if the speed of a particle is increasing?
-The speed of a particle is increasing when the velocity is either positive and increasing or negative and decreasing. This can be determined by looking at the graph of the velocity function or by analyzing the derivative (acceleration) of the velocity function.
What is the total distance traveled by a particle on a given time interval?
-The total distance traveled is found by integrating the absolute value of the velocity function over the time interval. This gives the net distance or the path length covered by the particle, regardless of direction.
How do you use u-substitution to integrate a function?
-U-substitution is a method used to integrate a function by substituting a part of the integrand with a new variable, u. The derivative of u with respect to x (du/dx) is then found, and the integral is rewritten in terms of u and du. This often simplifies the integral into a more manageable form that can be solved more easily.
Outlines
📚 Basic Integration Techniques
The video begins with a review of Unit 6, focusing on basic integration techniques. The first task is to integrate the function 3 + 2x - 4/x^2 with respect to x. This is done by finding the antiderivative of each term: 3x for the constant, x^2 for the linear term using the power rule, and 4/x by rewriting the term and applying the power rule. The process emphasizes the importance of including a constant of integration (+C). The video also covers integrating the derivative of cosine and sine functions, simplifying expressions before integrating, and applying properties of even and odd functions to evaluate definite integrals.
🧮 Definite Integrals and Function Properties
The script continues with problems involving definite integrals and properties of functions. It discusses how to calculate the integral of an even function (f(x)) from 0 to 4 and then from -4 to 4, doubling the result from the interval [0, 4] due to symmetry. For odd functions (G(x)), the integral over a symmetric interval around the origin equals zero. The video also tackles the integral of the difference of functions (G - f) and uses integral properties to simplify expressions. It concludes with calculating the integral of a constant times a function and the integral of a function over a reversed interval.
🏔 Evaluating Definite Integrals
The third paragraph deals with evaluating definite integrals. It covers finding the antiderivative of trigonometric functions like cosine and sine, and using the properties of these functions to evaluate the integral from 0 to π/4. The process involves substituting the upper and lower limits of integration into the antiderivative. The video also demonstrates how to evaluate definite integrals for functions like 2 - sin(x) from 0 to π/6 and 3 * (x^(1/2))/x from 1 to 9. It concludes with using a table of function values to evaluate definite integrals and emphasizes the importance of understanding the geometric interpretation of integrals.
❄ Snow Accumulation and Particle Motion
The script introduces a real-world application of integration by discussing the accumulation of snow at a rate R(t) inches per hour. It explains the units for differentiating the rate with respect to time (inches per hour squared) and integrating the rate over a time interval (inches). The video also explores the motion of a particle along the x-axis with a given velocity function V(t) and how to find the average velocity and position of the particle over a time interval. It concludes with calculating the total distance traveled by the particle and determining when the speed of the particle is increasing by analyzing the velocity graph.
🚗 Vehicle Velocity and Acceleration
The sixth paragraph involves a table showing the velocity of a vehicle at various times and uses it to estimate the acceleration at t = 1 hour. It explains that acceleration is the derivative of velocity or the average rate of change of velocity. The video then explores the concept of average acceleration and velocity over a time interval and the total distance traveled by the vehicle during a two-hour interval. It also discusses the limitations in determining the average velocity and total distance without the position function and how to interpret the integral of velocity in the context of the problem.
🔢 Approximating Area Under a Curve
The seventh paragraph focuses on approximating the area under a curve using Riemann sums. It explains how to use the midpoint and right-hand Riemann sums to estimate the integral of velocity from 0 to 2, which corresponds to the net distance traveled. The video also covers the concept of the average value of a function over an interval and how it relates to the average velocity of the vehicle on a given time interval. It concludes with finding the average value of a function f(x) = x^2 - sin(x) on the interval from 0 to π using the average value formula.
📐 Area and Antiderivatives
The eighth paragraph involves finding the difference between the values of a function (f(x)) at points 3 and 0, and at points 5 and -3, by setting up integrals and using the graph of the derivative function (f'(x)). It explains how the integral of the derivative function from points a to b equals the difference in the values of the original function (f(b) - f(a)). The video also covers calculating the value of a function at a specific point using the given value of the function at another point and an integral representing an area under the graph.
🧵 Substitution in Integration
The ninth paragraph delves into the method of u-substitution for integrating complex functions. It provides several examples where the integrand contains a root or a logarithmic expression. The video demonstrates how to choose an appropriate substitution (u) based on the structure of the integrand, perform the substitution, and then carry out the integration. It concludes with verifying the result by differentiating the antiderivative and ensuring it matches the original integrand.
📐 Definite Integrals and Function Evaluation
The tenth paragraph discusses the evaluation of definite integrals and function values using substitution and the properties of integrals. It covers finding the value of an integral from a to b by subtracting the value of the antiderivative at point a from the value at point b. The video also explores the concept of the average value of a function over an interval and how to approximate definite integrals using Riemann sums. It concludes with a discussion on the interpretation of integrals in the context of area and accumulation.
🧮 Advanced Substitution and Integration
The eleventh paragraph presents advanced examples of u-substitution for integration, including cases where the integrand involves square roots, cube roots, or exponential functions. The video demonstrates how to perform u-substitution, simplify the integrand, and carry out the integration. It also covers the use of the chain rule in differentiation and the importance of reverse substitution to express the final answer in terms of the original variable. The paragraph concludes with a reminder to check the solution by differentiating the antiderivative and comparing it with the original integrand.
📚 Final Integration Techniques
The twelfth paragraph concludes the video script with a discussion on various integration techniques, including substitution for terms involving square roots and exponential functions. It provides examples of how to perform integration by recognizing patterns that suggest suitable substitution variables. The video emphasizes the importance of simplifying the integrand after substitution and using the power rule for integration. It concludes with a reminder of the need for reverse substitution to express the integral in terms of the original variable.
Mindmap
Keywords
💡Antiderivative
💡Power Rule
💡Indefinite Integral
💡Even and Odd Functions
💡Integration by Parts
💡Average Value
💡Chain Rule
💡Riemann Sum
💡U-Substitution
💡Definite Integral
💡Velocity and Acceleration
Highlights
The video begins with a review of basic integration techniques, starting with integrating the function 3 + 2x - 4/x^2 with respect to x.
The antiderivative of 3 with respect to x is found to be 3x, using the power rule for the other terms.
For the term 4/x, the antiderivative is derived by recognizing the similarity to the derivative of 1/x.
The indefinite integral requires the addition of a constant term, denoted as +C.
Integration of the derivative of sine x is shown to be negative cosine x, and vice versa.
The technique of using the product rule for integration is discussed, along with its limitations.
The concept of even and odd functions is introduced with examples of how they affect the integral from -a to a.
The integral of a function multiplied by a constant is simplified using properties of integrals.
The average velocity of a particle is calculated using the integral of the velocity function over a time interval.
The concept of average acceleration is explained and calculated using the change in velocity over time.
The position of a particle at a future time is determined by integrating the velocity function.
The total distance traveled by a particle is found by integrating the absolute value of the velocity function.
The conditions for when the speed of a particle is increasing are determined by analyzing the velocity graph.
The velocity of a vehicle is used to estimate acceleration and average velocity using a table of values.
The average value of a function on a given interval is calculated using the average value formula.
The graph of a derivative function is used to find the difference in the antiderivative at two points.
U-substitution is applied to integrate complex functions, such as tan(4x)/(cos(4x))^2.
The method of integrating by parts is demonstrated for products of functions and their derivatives.
The final set of problems involves advanced integration techniques, including u-substitution and integration by parts.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: