Double Integrals

The Organic Chemistry Tutor

22 Oct 201925:02

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video tutorial delves into the evaluation of double integrals, focusing on the process of iterated integration. The instructor emphasizes the importance of recognizing variable bounds and the order of integration. Through step-by-step examples, the video demonstrates how to treat variables as constants when integrating with respect to one variable, and how to find antiderivatives for functions of y and x. It also explores the concept that changing the order of integration does not affect the final result, provided the variable bounds are correctly adjusted. The video concludes with a challenge problem, encouraging viewers to apply their understanding of double integrals and iterated integrals in a practical context.

Takeaways

📚 The video focuses on evaluating double integrals, specifically iterated integrals, by working from the inside integral outward.
🔢 The numbers in the integral correspond to the limits of integration, with '1 and 3' being y values and '0 and 2' being x values.
📉 When integrating with respect to y, x is treated as a constant, and the antiderivative of \( y^2 \) is \( \frac{y^3}{3} \).
📈 The process involves evaluating the antiderivative at the limits of integration and then simplifying the expression step by step.
🔄 The order of integration can be changed, and it's important to ensure that the limits of integration correspond correctly when doing so.
📝 The video demonstrates that changing the order of integration results in the same value for the integral, emphasizing the commutative property of iterated integrals.
📐 The script includes a problem involving a rectangular region R with specific x and y values, showing how to set up the integral in two ways.
🔑 U-substitution is introduced as a technique for solving more complex integrals, such as when the integrand involves expressions like \( x^2y \).
🧩 The video challenges viewers to solve a problem involving a double integral over a rectangular region defined by specific values for x and y.
📉 The final challenge problem involves integrating with respect to x first and then y, using u-substitution where u is \( x^2y \), and changing the order of integration for simplification.
🎓 The video concludes with a comprehensive explanation of how to work with double integrals and iterated integrals, highlighting the importance of methodical evaluation and correct application of calculus techniques.

Q & A

What are the key numbers to focus on when setting up a double integral from the given problem?
-The key numbers to focus on are the limits of integration, which in the script are 1 and 3 for y-values and 0 and 2 for x-values. These correspond to the bounds within which the integral is evaluated.
Why is it important to remember the order of dx and dy in a double integral?
-The order of dx and dy is crucial because it determines the order of integration. If dx is written later, the x-values are integrated first, and if dy is written later, the y-values are integrated first. This affects how you set up the integral and the resulting evaluation.
What is the antiderivative of y squared with respect to y?
-The antiderivative of y squared with respect to y is y cubed divided by 3. This is found by using the power rule for antiderivatives, which involves increasing the exponent by one and then dividing by the new exponent.
How does the value of a double integral change if the order of integration is reversed?
-The value of the double integral remains the same even if the order of integration is reversed, as long as the limits of integration correspond correctly to the new order. This is due to Fubini's theorem, which states that the value of a double integral is the same regardless of the order of integration.
What is the final result of the first double integral problem evaluated in the script?
-The final result of the first double integral problem is 52/3. This is obtained after evaluating the inner integral with respect to y and then the outer integral with respect to x.
How does changing the limits of integration affect the evaluation of a double integral?
-Changing the limits of integration will generally change the result of the double integral. The limits define the range over which the function is integrated, and different ranges will yield different areas under the curve, thus different integral values.
What substitution method is used in the script to simplify the evaluation of a double integral?
-The script uses u-substitution to simplify the evaluation of a double integral. This involves setting u equal to an expression involving the variables of integration and then differentiating with respect to one of the variables to find du/dx or du/dy.
Why might you choose to integrate with respect to y first instead of x in a double integral?
-You might choose to integrate with respect to y first if the expression inside the integral is simpler or if the resulting antiderivative is easier to find when y is the first variable of integration. This can make the problem easier to solve.
What is the significance of treating certain variables as constants during the integration process?
-Treating certain variables as constants during integration allows you to focus on integrating one variable at a time. This simplifies the process, as you can ignore the dependency of other variables on the one you are integrating with respect to.
How does the script demonstrate the use of u-substitution in double integrals?
-The script demonstrates u-substitution by setting u equal to an expression involving both x and y, then finding du/dx or du/dy, and finally replacing dx or dy with du/dx or du/dy in the integral. This substitution simplifies the integral and makes it easier to evaluate.
What is the final result of the challenge problem involving u-substitution and changing the order of integration?
-The final result of the challenge problem is 1/18 times e^18 minus 19. This is obtained after using u-substitution to simplify the integral and then evaluating it over the correct limits of integration.

Outlines

00:00

📚 Introduction to Double Integrals

This paragraph introduces the concept of double integrals and the process of evaluating an iterated integral. The focus is on understanding the order of integration, with the numbers 1 and 3 corresponding to y values and 0 and 2 to x values. The explanation walks through the steps of evaluating the integral from 1 to 3 of x times y squared with respect to y, treating x as a constant, and then finding the antiderivative of y squared. The process continues by evaluating the resulting expression from 0 to 2 with respect to x, ultimately leading to the final answer of 52/3. The paragraph also touches on the invariance of the double integral's value when the order of integration is changed, provided the limits of integration are correctly adjusted.

05:01

🔍 Evaluating Double Integrals with Variable Limits

The second paragraph delves into evaluating double integrals over a rectangular region R with given x and y values. It discusses the flexibility of writing the integral in two ways, either starting with x values or y values, and emphasizes the importance of maintaining the correct order of dx and dy. The summary includes a step-by-step calculation of an integral from 0 to 1 of (2y - 3x^2 * y^2)dx, simplifying the expression and finding the antiderivative for each term. The evaluation of the integral from 0 to 2 of (2y - y^2)dy follows, leading to the final answer of 4/3. The paragraph also presents a new problem for the viewer to solve, involving a different integral with a given rectangular region.

10:02

📈 Applying U-Substitution to Double Integrals

This paragraph introduces a method for solving more complex double integrals using u-substitution. It begins by defining a rectangular region with specific x and y values and setting up the integral with the y values first. The integral from 0 to 2 of (4x + y^3)dx is then tackled using u-substitution, where u is defined as 4x + y. The process involves differentiating u with respect to x to find dx in terms of du, and then simplifying the integral to u^3. The limits of integration are adjusted according to the values of x and y, leading to the antiderivative of u^4/4, which is then evaluated from y to 8 + y. The final step involves simplifying the expression and calculating the definite integral from 0 to 3, resulting in a complex arithmetic calculation that yields the final answer.

15:05

🧩 Changing the Order of Integration

The fourth paragraph discusses the strategy of changing the order of integration to simplify the evaluation of a double integral. It starts by questioning whether to differentiate u with respect to x or y and then demonstrates that differentiating with respect to x is more straightforward. The order of integration is reversed, and the integral is set up with x values first, leading to a new integral expression involving xy and e^(u). The limits of integration are adjusted accordingly, and the integral is simplified by recognizing that the derivative of e^(u) with respect to u is simply e^(u). The final expression is evaluated from 0 to 9y, yielding an exponential function minus a constant, which is then used to find the final answer for the integral.

20:07

🎓 Conclusion and Challenge Problem

In the concluding paragraph, the video script summarizes the process of working with double integrals and iterated integrals, emphasizing the importance of understanding the order of integration and the limits of integration. It also presents a challenge problem for the viewer to practice the skills learned in the video. The challenge involves using u-substitution to evaluate an integral where u is set to x^2 times y, and the differentiation is done with respect to x. The video encourages the viewer to work through the problem and understand the process of changing the order of integration and applying u-substitution. The script ends with a reminder to subscribe to the channel for more educational content.

Mindmap

Keywords

💡Double Integrals

Double integrals are a fundamental concept in calculus that extend the idea of a single integral to functions of two variables. They allow for the calculation of quantities such as volume, surface area, or the average value of a function over a two-dimensional region. In the video, the main theme revolves around evaluating double integrals, with the script providing step-by-step instructions on how to do so, demonstrating the process with various integrals written on the board.

💡Iterated Integral

An iterated integral is a way to evaluate a double integral by integrating with respect to one variable at a time. The script emphasizes the importance of the order of integration, showing that the integral can be evaluated by working from the inside out, first integrating with respect to y and then x, or vice versa. The video script provides examples of iterated integrals and demonstrates how to evaluate them correctly.

💡Antiderivative

The antiderivative, also known as the integral, is a function that represents the reverse process of differentiation. It is used to find the area under a curve or to calculate the cumulative effect of a rate of change. In the context of the video, the antiderivative is used to find the indefinite integral of functions such as y^2 and x, which are then evaluated over specific intervals to find the definite integral.

💡Order of Integration

The order of integration refers to the sequence in which the variables are integrated in an iterated integral. The video script explains that changing the order of integration can sometimes simplify the process or make it more complex, depending on the function and the limits of integration. The script provides an example where the order is switched and shows that the value of the integral remains the same.

💡Constants

In the context of integration, constants are terms that do not change with respect to the variable being integrated. The script mentions treating certain terms as constants, such as '2y' or 'y^2', when integrating with respect to another variable. This simplifies the integration process, as constants can be factored out of the integral and then multiplied by the antiderivative of the remaining expression.

💡Limits of Integration

Limits of integration are the boundaries within which an integral is evaluated. They define the region over which the function is integrated. The video script provides specific examples of limits, such as integrating from 0 to 2 with respect to x and from 1 to 3 with respect to y, and demonstrates how these limits are used to calculate the value of the integral.

💡U-Substitution

U-substitution is a technique used in calculus to simplify the process of integration, especially when dealing with complex functions. In the video, u-substitution is introduced as a method to evaluate more complicated integrals by letting u be an expression involving the original variables, thus transforming the integral into a more manageable form. The script provides an example where u is set to 4x + y, and the process of differentiating u with respect to x is shown.

💡Rectangular Region

A rectangular region in the context of double integrals refers to the area in the xy-plane that is bounded by the limits of integration. The video script describes how to set up double integrals over a rectangular region by identifying the x and y limits, which correspond to the sides of the rectangle. This region is used to visualize and calculate the integral's value.

💡Exponential Function

An exponential function is a mathematical function of the form f(x) = a * b^(x), where b is a constant and a is the coefficient. In the video, the exponential function e^(u) is used within an integral, and the antiderivative of this function is e^(u) itself, as demonstrated in the script. The exponential function is a key component in one of the challenge problems presented in the video.

💡Challenge Problem

A challenge problem in the video is an advanced or more complex integral that the viewer is encouraged to solve on their own. The script presents a challenge problem involving an exponential function and a double integral with a u-substitution. It serves as a practical application of the concepts taught in the video and tests the viewer's understanding and ability to apply these concepts to solve more difficult problems.

Highlights

Introduction to the concept of double integrals and iterated integrals.

Explanation of how to interpret the order of integration based on the placement of dx and dy.

Step-by-step evaluation of an iterated integral with a focus on treating variables as constants during integration.

Finding the antiderivative of y squared and evaluating it within the given limits.

Demonstration of how to handle multiple variables in an integral by specifying their ranges.

Calculation of the final answer for the first integral, emphasizing the process of constant factoring and variable substitution.

Discussion on the impact of changing the order of integration and its effect on the integral's value.

Evaluation of a second integral by integrating with respect to x first, treating y squared as a constant.

Explanation of the antiderivative process for x to the first power and subsequent evaluation.

Illustration of the principle that the value of double integrals remains the same regardless of the order of integration.

Presentation of a problem involving a rectangular region and the double integral's representation in two ways.

Solution of a double integral with the expression 2y - 3x^2y^2, including variable substitution and simplification.

Introduction of a challenge problem and the strategy for tackling it, such as choosing the order of integration.

Application of u-substitution to simplify the integral and the process of differentiating with respect to x.

Final calculation of a complex double integral using u-substitution and changing the order of integration.

Conclusion summarizing the ability to work with double integrals and evaluate iterated integrals.

Transcripts

Browse More Related Video

Iterated Integrals (Introduction to Multiple Integrals)

Lec 16: Double integrals | MIT 18.02 Multivariable Calculus, Fall 2007

Changing the Order of Integration (Double Integrals)

_-substitution: definite integrals | AP Calculus AB | Khan Academy

Double integrals 6 | Double and triple integrals | Multivariable Calculus | Khan Academy

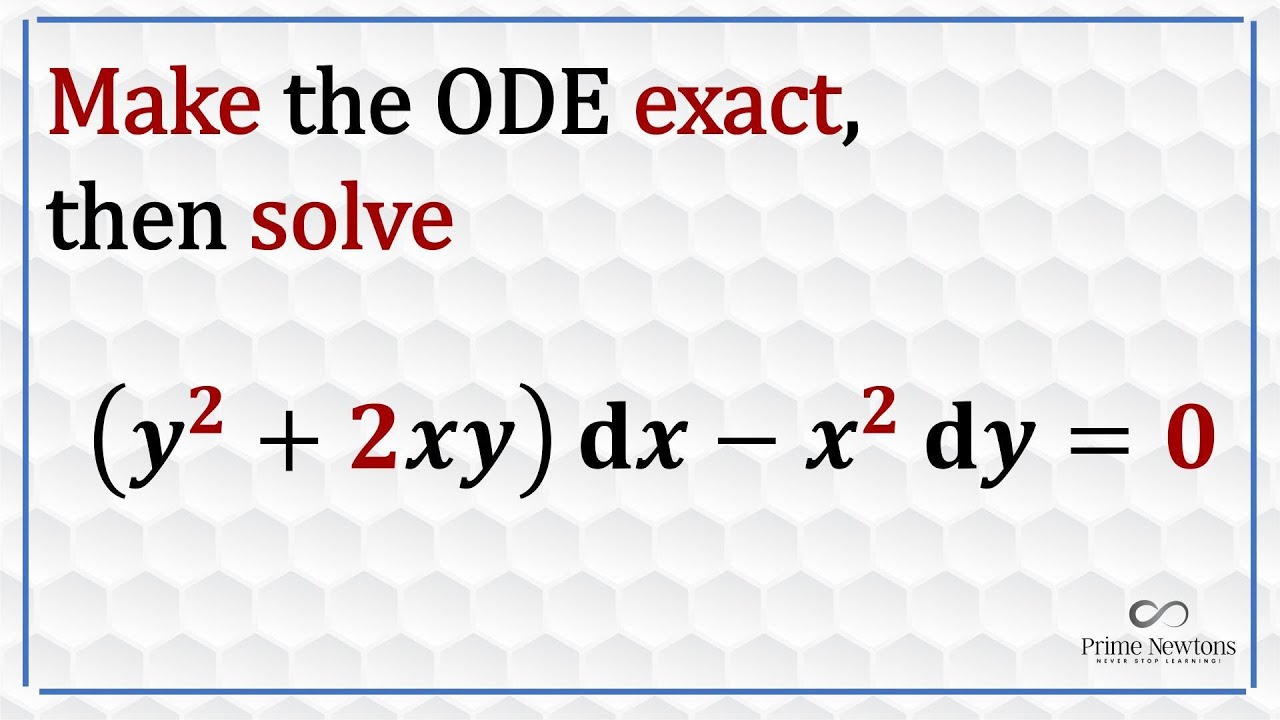
How to solve exact and non-exact ODE

Related Tags

Double Integrals Iterated Integrals Mathematics Calculus Antiderivative Integration Educational Tutorial Math Help Problem Solving