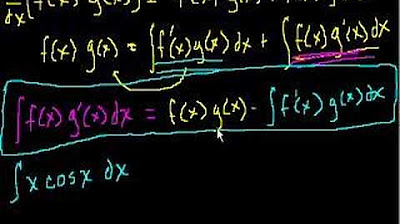Calculus 2 Lecture 7.1: Integration By Parts
TLDRThis video script delves into advanced integral calculus techniques, focusing on the concept of integration by parts, a method for integrating products of functions. The instructor introduces the product rule for derivatives and its inverse, leading to the integration by parts formula. Through step-by-step examples, the script illustrates how to apply this formula to solve complex integrals, emphasizing the importance of correctly choosing the function to integrate and differentiate. It also touches on trigonometric identities and the reduction formula for simplifying integrals involving powers of sine functions, offering a comprehensive guide to tackling challenging integral problems.
Takeaways
- 📚 The script introduces new integration techniques beyond the basic methods of using an integration table or substitution.
- 🔄 It explains the concept of integration by parts, which is analogous to the product rule in differentiation but in reverse.
- 🤔 The script raises the question of why there isn't a product rule for integrals, highlighting the uniqueness of the integration by parts technique.
- 📈 The process of integrating by parts involves selecting a function to be 'u' in such a way that its derivative simplifies or becomes more manageable.
- 📉 The 'v' function is what remains after selecting 'u', and it should be something that can be easily integrated.
- 🧩 The formula for integration by parts is presented as a way to break down complex integrals into simpler parts, involving the product of 'u' and 'v' minus the integral of 'v' with respect to the derivative of 'u'.
- 🔢 The script provides examples to illustrate the process of integration by parts, emphasizing the importance of correctly choosing 'u' and 'v' to simplify the integral.
- ♻️ The concept of repetitiveness in integration by parts is introduced, where the integral of a product of functions can sometimes return a similar expression, requiring additional steps to solve.
- 📝 The importance of checking for integrals in the table and attempting substitution before resorting to integration by parts is emphasized for efficiency.
- 🔍 The script discusses the use of trigonometric identities to simplify integrals involving secant and tangent functions, showcasing the need for a deep understanding of algebraic manipulation and trigonometry.
- 📉 The reduction formula is introduced as a method to simplify the integration of high powers of trigonometric functions, effectively reducing the power and making the integral more approachable.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is integration techniques, specifically focusing on integration by parts and the reduction formula for integrals involving trigonometric functions.
What is the purpose of introducing integration by parts in the lecture?
-The purpose of introducing integration by parts is to provide a method for integrating functions that do not fit the integration table and cannot be easily integrated using basic substitution.
How does the product rule for derivatives relate to integration by parts?
-Integration by parts is the inverse process of the product rule for derivatives. While the product rule expands the derivative of a product of two functions into a sum of two terms, integration by parts breaks down the integral of a product of two functions into a sum of two integrals.
What is the general process for choosing U and V when using integration by parts?
-When using integration by parts, you should choose U in such a way that its derivative makes the resulting expression simpler or easier to integrate, and choose V such that the integral of V is straightforward or possible.
What is the significance of the reduction formula in integral calculus?
-The reduction formula is significant because it allows for the simplification of integrals involving high powers of trigonometric functions by reducing the power, making the integral more manageable.
How does the lecturer demonstrate the application of integration by parts?
-The lecturer demonstrates the application of integration by parts by working through several examples, including integrals of products of functions and functions raised to powers, showing step-by-step calculations and explaining the reasoning behind each step.
What is the integral of ln(x) from 1 to e, and why is this result interesting?
-The integral of ln(x) from 1 to e is exactly 1. This result is interesting because it shows that the area under the curve of ln(x) between these two points is a precise value, which is a unique property of the natural logarithm function.
What is the condition for using the reduction formula for trigonometric integrals?
-The reduction formula for trigonometric integrals can be used when the integral involves a trigonometric function raised to a power greater than or equal to two.
How does the lecturer handle the case when the integral of a function results in a similar form as the original function?
-When the integral results in a similar form as the original function, the lecturer suggests adding the integral to both sides of the equation and then dividing by the coefficient to eliminate the integral, simplifying the problem.
What is the final step in solving an indefinite integral after applying the reduction formula?
-The final step in solving an indefinite integral after applying the reduction formula is to add the constant of integration, denoted by 'C', to account for any constant that may have been lost during the integration process.
Outlines
📚 Introduction to Advanced Integration Techniques
The speaker introduces chapter 7, section 7.1, emphasizing the limitations of basic integration methods and the need for more advanced techniques. They highlight the use of substitution when the integral fits the integration table and the necessity of learning new methods for more complex integrals. The concept of the chain rule in derivatives is compared to a potential product rule in integrals, sparking curiosity about the upcoming lesson on integration by parts.
🔍 Exploring the Product Rule in Integrals
The video script delves into the product rule for derivatives and its inverse operation in integrals. The speaker demonstrates the mathematical process of integrating both sides of the product rule equation, leading to the introduction of integration by parts. They explain the process of separating the integral into two parts and the importance of choosing the correct function to integrate and differentiate, using the commutativity of multiplication to simplify the expression.
📝 The Integration by Parts Process
The speaker outlines the steps of integration by parts, emphasizing the algebraic manipulation involved in the process. They introduce the use of symbols U and V to represent functions in the integral and demonstrate the substitution process with these symbols. The explanation includes the importance of choosing U such that its derivative simplifies the expression, and the integral of V is feasible, leading to the formula for integration by parts.
🔢 Practical Application of Integration by Parts
The script provides a practical example of integration by parts using the integral of x * e^x. The speaker guides the audience through the process of choosing U and V, performing the integration and differentiation, and applying the integration by parts formula. They highlight the importance of simplifying the expression and the potential for making algebraic mistakes, emphasizing the need for careful work.
📉 Integration by Parts: Choosing U and V
The speaker discusses the strategy for choosing U and V in integration by parts, suggesting that U should be chosen to simplify the derivative and make the integral of V possible. They provide a note on choosing U to reduce the power of the function and use an integral example to illustrate the process, cautioning against incorrect choices that complicate the integral.
📌 Correctly Applying Integration by Parts
The script emphasizes the importance of correctly applying integration by parts, with a focus on simplifying the expression and correctly identifying U and V. The speaker uses an example involving a natural logarithm and a cubic function to demonstrate the process, highlighting the need to ensure that the integral of V is doable and that the derivative of U is simpler.
🔁 The Repetitive Nature of Integration by Parts
The speaker discusses the repetitive nature of integration by parts, using an example with sine and cosine functions. They show that the process can lead back to the original expression, indicating a loop in the integration process. The explanation includes the steps of integration by parts and the importance of recognizing when the process repeats, suggesting a need for a different approach if the integral does not simplify.
🎯 Solving Integrals with Trigonometric Identities
The script introduces the use of trigonometric identities to simplify integrals involving secant and tangent functions. The speaker demonstrates how to break down complex integrals into parts that can be more easily integrated, using identities to transform tangent into secant and vice versa, and emphasizing the importance of recognizing patterns in the integral.
📚 The Power of Trigonometric Identities in Integration
The speaker continues to explore the use of trigonometric identities in integration, showing how to simplify the integral of secant cubed times tangent. They use the identity for tangent squared and demonstrate the process of distributing and separating integrals, highlighting the importance of algebraic manipulation in the integration process.
📉 Integration by Parts with Trigonometric Functions
The script provides an example of using integration by parts with trigonometric functions, specifically focusing on the integral of secant to the fifth power. The speaker guides the audience through the process of breaking down the integral, using trigonometric identities, and applying integration by parts multiple times to simplify the expression.
📝 The Reduction Formula for Trigonometric Integrals
The speaker introduces the reduction formula for integrals involving powers of sine or cosine. They explain the process of creating a formula to simplify the integration of higher powers of trigonometric functions, using integration by parts and algebraic manipulation to reduce the power of the sine function in the integral.
🔢 Applying the Reduction Formula to Sine Integrals
The script demonstrates the application of the reduction formula to the integral of sine raised to the fourth power. The speaker shows how to use the formula to reduce the power of the sine function and simplify the integral, emphasizing the efficiency of this method compared to repeated integration by parts.
📌 Final Thoughts on Section 7.1
The speaker concludes section 7.1 by summarizing the key points covered in the video, including advanced integration techniques, the product rule in integrals, the process of integration by parts, and the reduction formula for trigonometric integrals. They highlight the importance of practice and understanding the process, encouraging students to work through examples to gain proficiency.
Mindmap
Keywords
💡Integrals
💡Integration Table
💡Substitution
💡Chain Rule
💡Product Rule
💡Integration by Parts
💡Derivative
💡Trigonometric Functions
💡Reduction Formula
💡Definite Integral
Highlights
Introduction of new integration techniques beyond the basic integration table and substitution.
Explanation of the product rule for derivatives and its inverse process for integrals.
Derivation and proof of the integration by parts formula from the product rule.
Illustration of how to apply integration by parts to non-standard integrals.
Guidance on choosing the correct function for 'u' and 'dv' in integration by parts.
Application of integration by parts to the integral of x * e^x dx as an example.
Demonstration of the integration by parts process with multiple examples to solidify understanding.
Use of integration by parts to solve integrals that do not fit the basic integration table or substitution methods.
Mistake demonstration during the integration by parts process to highlight common errors.
Strategy for tackling integrals that do not match the integration table or substitution criteria.
The concept of 'u' making the derivative better and the integral of 'v' being possible as criteria for choosing 'u' in integration by parts.
Detailed walkthrough of an example using integration by parts to emphasize the step-by-step process.
Reduction of complex integrals into more manageable parts using integration by parts.
Integration by parts applied to trigonometric functions and the use of trigonometric identities to simplify the process.
Final walkthrough of a complex integral problem using integration by parts to demonstrate the comprehensive process.
Introduction to the reduction formula for integrals involving powers of sine or cosine functions.
Proof and explanation of the reduction formula for powers of sine, making integration by parts more efficient.
Application of the reduction formula to an example integral to demonstrate its utility in simplifying the integration process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: