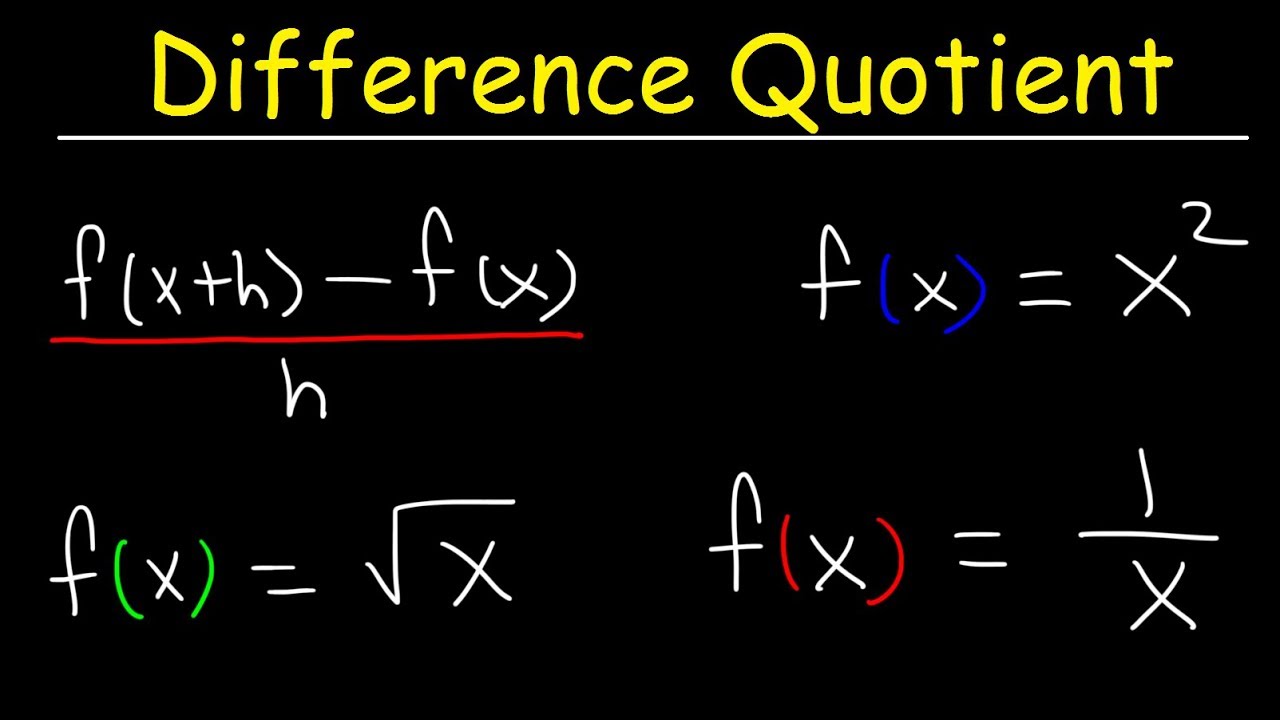The Difference Quotient!
TLDRIn this engaging video, Ian breaks down the concept of the difference quotient, a mathematical tool used to estimate the slope of a function between two points. Starting with an introduction to functions, he uses the analogy of 'star notation' to simplify the understanding of function notation. Ian then delves into the historical context of the difference quotient, illustrating its relevance with a graph and explaining how it can be used to find the average rate of change between two points on a function. The video continues with a step-by-step guide on calculating the difference quotient for a given function, emphasizing the importance of correctly identifying f(x+h), distributing the negative sign, and ensuring the cancellation of the variable 'h'. Ian reinforces learning by tackling a more complex function, demonstrating the process of simplifying fractions and the importance of finding a common denominator. The video concludes with key takeaways, encouraging viewers to apply the 'pattern game' for function notation, double-check their work, and ensure the correct application of algebraic rules. Ian's approach makes the difference quotient less intimidating and more accessible to learners.
Takeaways
- 📚 The concept of the difference quotient is introduced as a way to find the slope between two points on a function.
- 🔍 Understanding functions is fundamental to grasping the difference quotient, with the function notation being a key aspect.
- 🌟 The pattern game is used as a metaphor for understanding how to substitute variables within functions, simplifying the process.
- ✅ The function f(x) = x^2 + 2x is used as an example to demonstrate how to apply the difference quotient formula.
- 📈 Historical insight is provided into the origin of the difference quotient, relating it to the concept of average rate of change.
- 📝 The formula for the difference quotient is derived from the slope formula, emphasizing the substitution of variables and simplification.
- 🚀 The process of simplifying the difference quotient involves careful algebraic manipulation, ensuring that terms cancel out as expected.
- 💡 It's emphasized to double-check the substitution of f(x + h), the distribution of the negative sign, and the cancellation of terms.
- 📉 A more complex function, f(x) = -1/x, is used to illustrate the process of finding and simplifying the difference quotient.
- 🎯 The importance of finding a common denominator when adding fractions is highlighted, which is crucial for simplifying the quotient.
- ✋ The final simplified form of the difference quotient is obtained by canceling out terms and combining fractions, resulting in a simplified expression.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the concept of the difference quotient in mathematics, including its definition, application, and how to work with it in the context of functions.
What is the difference quotient?
-The difference quotient is a mathematical expression used to find the slope between two points on a function. It is represented as (f(X + H) - f(X)) / H, where f(X) is a function and H is the step taken to the right from point X.
How does the video explain the concept of functions?
-The video explains functions by using the notation f(X), where X is an input and f(X) is the corresponding output. It also uses a 'star' notation to help visualize the process of substituting values into the function.
What is the purpose of using the 'star' notation in the explanation?
-The 'star' notation is used as a substitute for X to help visualize the process of substituting different values into a function. It simplifies the understanding of how functions work by removing the potential confusion of repeated X's.
How does the video approach simplifying the difference quotient?
-The video approaches simplifying the difference quotient by first ensuring that f(X + H) is correctly identified and substituted, then by distributing the negative sign correctly, and finally by simplifying the algebraic expression to cancel out the H in the denominator, if possible.
What are the key steps to follow when working with the difference quotient?
-The key steps are: 1) Correctly finding f(X + H) by substituting (X + H) into the function, 2) Distributing the negative sign when subtracting f(X) from f(X + H), and 3) Simplifying the expression to cancel out the H in the denominator, which is a sign that the previous steps were done correctly.
Why is it important to remember the parentheses when subtracting f(X) from f(X + H)?
-Remembering the parentheses is important because it ensures that the entire function f(X) is being subtracted, not just the part without the parentheses. This prevents mistakes that could lead to incorrect cancellation and an incorrect final answer.
What is the significance of the historical insight provided in the video?
-The historical insight provided in the video helps to contextualize the difference quotient within the broader field of mathematics. It shows how the concept is used to find the average rate of change between two points on a graph, which is a fundamental question in mathematics and physics.
How does the video use a simple function to illustrate the difference quotient?
-The video uses the simple function f(X) = 2X + 4 to demonstrate the process of finding and simplifying the difference quotient. By substituting (X + H) into the function and following the steps outlined, the video shows how to simplify the expression to reveal the final answer.
What is the final answer obtained for the difference quotient of the function f(X) = 2X + 4?
-The final answer obtained for the difference quotient of the function f(X) = 2X + 4 is 2, after simplifying the expression and canceling out the H in the denominator.
What is the advice given for someone who is having difficulty with the concept of the difference quotient?
-The advice given is to remember the pattern game for substituting (X + H) into the function, to double-check each step, and to ensure that the H in the denominator cancels out, which is a sign that the process has been done correctly. If the H does not cancel out, it suggests that there may have been a mistake in the previous steps.
What is the purpose of checkpoints in the process of simplifying the difference quotient?
-Checkpoints serve as a way to verify that each step of the process has been completed correctly. They help to ensure that f(X + H) is accurately found, that the negative sign is properly distributed, and that the final expression results in the cancellation of the H in the denominator, leading to the correct simplification.
Outlines
😀 Introduction to the Difference Quotient
Ian introduces the topic of the difference quotient, explaining its purpose and aiming to simplify the concept for the audience. He begins with a basic function, f(x) = x^2 + 2x, and demonstrates how to evaluate the function using different notations, such as replacing 'x' with a star. The focus is on understanding the concept of functions and how they transform input values into output values.
🔍 Finding the Slope Between Two Points
The script explores the concept of finding the slope between two points on a function graph, which is also known as the average rate of change. Ian explains the formula for calculating slope and applies it to two points on a function. He then generalizes the process by considering a variable x and an increment h, leading to the definition of the difference quotient as the slope between points x and x + h on the function.
📚 Simplifying the Difference Quotient
Ian walks through the process of simplifying the difference quotient for a given function, f(x) = 2x + 4. He emphasizes the importance of correctly identifying f(x + h) and ensuring that parentheses are used to avoid common mistakes. The process involves distributing the negative sign and simplifying the expression to the point where the variable h can be canceled out, resulting in a simplified form of the difference quotient.
🤔 Tackling a More Complex Function
The video script presents a more complex function, f(x) = -1/x, and guides the audience through finding and simplifying its difference quotient. Ian recommends using parentheses for clarity and emphasizes the importance of simplifying the numerator before addressing the denominator. The process involves finding a common denominator, adding fractions, and canceling out terms to arrive at a simplified form of the difference quotient.
🏁 Final Tips and Checkpoints
Ian concludes with final tips for working with difference quotients. He advises the audience to remember the 'pattern game' for substituting x + h into the function and to double-check each step of the process. The checkpoints include ensuring the correct identification of f(x + h), distributing the negative sign accurately, and looking for opportunities to cancel out the variable h. The goal is to make the process of finding and simplifying difference quotients less intimidating and more approachable.
Mindmap
Keywords
💡Difference Quotient
💡Function
💡Slope
💡Average Rate of Change
💡Function Notation
💡Pattern Game
💡Algebraic Simplification
💡Cancelling
💡Derivative
💡Historical Insight
💡Common Denominator
Highlights
Introduction to the difference quotient, explaining its purpose and simplifying the understanding of the concept.
Understanding functions as the basis for the difference quotient, using the example f(x) = x^2 + 2x.
The use of a 'star' notation to simplify the concept of functions and their application.
Demonstration of how to calculate f(2) and f(2 + h) using the given function as an example.
Historical insight into the origin of the difference quotient and its connection to the concept of slope.
The generalization of finding the slope between two points on a function using an arbitrary first point 'x'.
The formula for the difference quotient is derived as the slope between two points, x and x + h.
Simplification of the difference quotient for the function f(x) = 2x + 4, resulting in a final answer of 2.
Emphasis on the importance of correctly identifying f(x + h), distributing the negative, and ensuring the cancellation of 'h'.
Approach to finding and simplifying the difference quotient for a more complex function, f(x) = -1/x.
Use of common denominators to simplify the expression and the process of combining fractions.
Final simplification of the difference quotient to 1/(x(x + h)) for the complex function example.
Advice on checkpoints to ensure the correct application of the pattern game and algebraic steps.
Encouragement to challenge oneself with more complex problems to improve understanding and skill.
Summary of the key steps and checkpoints for finding and simplifying difference quotients.
The importance of ensuring the cancellation of 'h' as a final check for the correct application of the process.
Closing remarks, reinforcing the goal of making difference quotients less intimidating and providing important notes for practice.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: