How to Use the Unit Circle in Trigonometry (Precalculus - Trigonometry 7)

Professor Leonard

25 Mar 202142:57

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers an in-depth exploration of the unit circle and its application in understanding trigonometric functions. The presenter explains how the unit circle, with a radius of one, allows for the easy correlation between arc length, radian measurements, and the sine and cosine values of angles. The script delves into finding the sine, cosine, and tangent for various angles, including coterminal angles and angles beyond one full revolution. It also covers the reciprocal trigonometric functions—cosecant, secant, and cotangent—emphasizing the importance of understanding their derivation from the primary functions. The video encourages viewers to practice using the unit circle to enhance their grasp of trigonometric concepts and to eventually rely less on the visual aid, building a strong foundation for more advanced mathematical studies.

Takeaways

📐 **Unit Circle Basics**: The unit circle has a radius of one and is used to define trigonometric functions for different angles.
🔵 **Sine and Cosine**: Sine corresponds to the y-coordinate and cosine to the x-coordinate of a point on the unit circle.
🔴 **Quadrants and Signs**: The signs of sine, cosine, and tangent vary depending on the quadrant in which the angle lies.
🔄 **Coterminal Angles**: Angles that differ by full rotations (multiples of 2π or 360 degrees) are coterminal and share the same trigonometric function values.
🔽 **Negative Angles**: Negative angles can be converted to positive coterminal angles for calculation purposes by counting in the clockwise direction.
🔃 **Rotation and Quadrants**: Angles can be located by counting rotations and identifying the correct quadrant on the unit circle.
🧮 **Tangent Calculation**: Tangent is found by dividing the sine (y-coordinate) by the cosine (x-coordinate) of the angle.
🔗 **Reciprocal Trigonometric Functions**: The reciprocal functions cosecant, secant, and cotangent are derived by taking the reciprocal of sine, cosine, and tangent respectively.
➗ **Rationalizing Denominators**: When dealing with square roots in trigonometric function values, rationalizing the denominator is often necessary to simplify the expression.
🔢 **Calculator Usage**: For angles not directly on the unit circle, a calculator can be used to find the sine, cosine, and tangent, ensuring the correct mode (degrees or radians) is selected.
📉 **Graphing and Periodicity**: Understanding the unit circle helps in graphing trigonometric functions and recognizing their periodic nature.

Q & A

What is a unit circle?
-A unit circle is a circle with a radius of one unit of length. It is commonly used in trigonometry to define the sine, cosine, and tangent of an angle, where these functions correspond to the y-coordinate, x-coordinate, and the ratio of the y-coordinate to the x-coordinate of a point on the circle, respectively.
How can the unit circle help in understanding coterminal angles?
-The unit circle helps in understanding coterminal angles by showing that angles that differ by full rotations (multiples of 2π radians or 360 degrees) end at the same point on the circle, thus having the same sine, cosine, and tangent values.
What is the relationship between sine and the y-coordinate on the unit circle?
-The sine of an angle in the unit circle is equal to the y-coordinate of the point where the terminal side of the angle intersects the circle.
How is cosine related to the x-coordinate on the unit circle?
-The cosine of an angle in the unit circle is equal to the x-coordinate of the point where the terminal side of the angle intersects the circle.
What is the process to find the tangent of an angle using the unit circle?
-To find the tangent of an angle using the unit circle, you divide the sine (y-coordinate) by the cosine (x-coordinate) of that angle's point on the circle.
How do you find the reciprocal trigonometric functions, such as cosecant, secant, and cotangent?
-The reciprocal trigonometric functions are found by taking the reciprocal (or inverse) of the basic trigonometric functions: cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.
What is the significance of the quadrant in which an angle is located on the unit circle?
-The quadrant in which an angle is located determines the signs of the sine, cosine, and tangent values for that angle. Each quadrant has specific signs for these trigonometric functions based on the signs of the x and y coordinates.
How can you find the trigonometric functions of an angle greater than one full revolution (e.g., 8π/3)?
-For angles greater than one full revolution, you can subtract multiples of 2π (or 360 degrees) from the angle until you get an equivalent angle between 0 and 2π (or 0 and 360 degrees), which will have the same trigonometric function values due to the periodic nature of the functions.
What is the process to find the trigonometric functions of a negative angle?
-To find the trigonometric functions of a negative angle, you can find its coterminal positive angle by adding multiples of 2π (or 360 degrees) until you get an angle within the standard range, and then use the unit circle to find the values as you would for a positive angle.
Why is it important to understand the unit circle before moving on to more advanced math courses?
-Understanding the unit circle is crucial because it provides a visual and conceptual foundation for trigonometric functions. As you progress to more advanced math courses like calculus, the ability to recall and apply these functions without constant reference to the unit circle becomes necessary.
How can you use a calculator to find the sine and cosine of angles not found on the unit circle?
-You can use a calculator to find the sine and cosine of any angle by ensuring the calculator is set to the correct mode (degrees or radians) and then entering the angle and pressing the corresponding function key (sin or cos).

Outlines

00:00

📐 Introduction to the Unit Circle

The video begins with an introduction to the unit circle, a fundamental tool in trigonometry. The presenter explains how the unit circle can be used to find the values of trigonometric functions for various angles. The video covers how to work with coterminal angles, which are angles that differ by full rotations, and how to interpret sine and cosine in terms of the coordinates of points on the circle. It also discusses the relationship between the radius of the unit circle and the arc length and radian measure of angles.

05:01

🔢 Calculating Trigonometric Functions

The presenter demonstrates how to calculate sine, cosine, and tangent for the angle 2 pi over 3, emphasizing the importance of understanding the underlying math rather than just memorizing values. The process involves creating a right triangle from the angle's coordinates on the unit circle and using the signs of the coordinates to determine the signs of the trigonometric functions. The video also explains how to find the reciprocal trigonometric functions, such as cosecant, secant, and cotangent.

10:02

🔁 Coterminal Angles and Trigonometric Function Reciprocity

The video explores coterminal angles, which are angles that have the same trigonometric function values due to being an integer multiple of 2 pi apart. The presenter shows that the trig functions for 8 pi over 3 are identical to those for 2 pi over 3. The concept of period is introduced, which is the interval after which the trig functions repeat their values. The video also covers the trig functions for pi over 4, highlighting that all trig functions in the first quadrant are positive.

15:02

🤔 Understanding Signs of Trigonometric Functions

The presenter discusses the signs of trigonometric functions in different quadrants, emphasizing the importance of knowing the quadrant to determine the sign of each function. The video provides an example calculation for the angle 7 pi over 6, explaining how to find the sine, cosine, and tangent, as well as their reciprocals. Rationalization of denominators is also covered, which is a common step in simplifying trigonometric expressions.

20:03

🔄 Dealing with Non-Unit Circle Angles

The video explains how to handle angles that do not lie on the unit circle by using the radius of the triangle formed by the angle. The presenter demonstrates how to find the radius and then use it to calculate the sine, cosine, and tangent for an angle in a right triangle. The process involves dividing the coordinates by the radius to align with the unit circle concept and maintain the correct signs for the trigonometric functions.

25:04

🧮 Using a Calculator for Non-Standard Angles

The presenter advises on the use of a calculator for finding trigonometric function values for angles not found on the unit circle, such as 28 degrees. It is emphasized to ensure the calculator is in the correct mode (degrees or radians) before proceeding with calculations. The video also touches on the difference between degrees and radians, and how to convert between them for calculator use.

30:06

📐 Final Thoughts on Trigonometry and the Unit Circle

The video concludes with a summary of the key points covered, including the use of the unit circle for finding trigonometric function values, the concept of coterminal angles, and the importance of understanding the underlying mathematical principles. The presenter encourages practice and emphasizes the utility of the unit circle in grasping the periodic nature of trigonometric functions.

Mindmap

Keywords

💡Unit Circle

A unit circle is a circle with a radius of 1 unit. It is a fundamental concept in trigonometry that allows us to define and understand the relationships between angles and their corresponding sine, cosine, and tangent values. In the video, the unit circle is used to explain how to find the trigonometric functions of various angles by identifying their coordinates on the circle.

💡Coterminal Angles

Coterminal angles are angles that share the same terminal side. They occur when an angle is measured in multiples of a full rotation (360 degrees or 2π radians). The video discusses how angles like 2π/3 and 8π/3, despite differing in their count of full rotations, result in the same sine, cosine, and tangent values because they terminate at the same point on the unit circle.

💡Radians

Radians are a unit of angular measure where the length of an arc is proportional to the radius. One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. In the video, radians are used to measure angles on the unit circle, allowing for a direct relationship between arc length and the sine and cosine values.

💡Sine Function

The sine function, often abbreviated as 'sin', is a trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right triangle or, in the context of the unit circle, the y-coordinate of a point on the circle to the radius. The video explains that sine can be found by looking at the y-coordinate of the point where an angle terminates on the unit circle.

💡Cosine Function

The cosine function, abbreviated as 'cos', is another trigonometric function that relates the ratio of the adjacent side to the hypotenuse in a right triangle or, in terms of the unit circle, the x-coordinate of a point on the circle to the radius. The video demonstrates that cosine values can be identified by the x-coordinate of the point corresponding to an angle on the unit circle.

💡Tangent Function

The tangent function, denoted as 'tan', is the ratio of the sine to the cosine of an angle. It is the ratio of the y-coordinate to the x-coordinate of a point on the unit circle. The video illustrates how to calculate the tangent by dividing the sine value (y-coordinate) by the cosine value (x-coordinate) for a given angle.

💡Reciprocal Trigonometric Functions

Reciprocal trigonometric functions are the inverses of the primary trigonometric functions (sine, cosine, and tangent). They include cosecant (csc), secant (sec), and cotangent (cot). The video explains how to find these functions by taking the reciprocal of the respective primary function, and it also covers the process of rationalizing the denominator when necessary.

💡Quadrants

Quadrants refer to the four equal parts of a plane that are divided by the two axes (x and y). In the context of the unit circle, each quadrant represents a different range of angles and is associated with the signs of the sine, cosine, and tangent values within that range. The video discusses how the signs of trigonometric functions change depending on which quadrant the angle is in.

💡Arc Length

Arc length is the distance along the path of an arc. On the unit circle, the arc length is directly related to the angle measured in radians. The video script mentions arc length in the context of relating it to radian degree measurements of angles, which helps in understanding the relationship between angles and their sine and cosine values.

💡Rationalizing Denominators

Rationalizing denominators is the process of eliminating a radical (square root) from the denominator of a fraction. This is often done to simplify expressions and avoid ambiguity. In the video, the presenter demonstrates how to rationalize the denominator when finding the cosecant and secant of certain angles, ensuring that the final answer is expressed as a rational number.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all values of the variables involved. They are used to simplify and manipulate trigonometric expressions. The video touches on the concept of trigonometric identities when discussing how the sine, cosine, and tangent functions repeat every 2π radians, which is a fundamental identity in trigonometry.

Highlights

Introduction to the unit circle and its application in understanding trigonometric functions.

Explanation of how the unit circle allows for easy correlation between arc length, radian degree measurements, and sine/cosine values.

Demonstration of how sine corresponds to the y-coordinate and cosine to the x-coordinate of a point on the unit circle.

Color-coded quadrants to indicate when each trigonometric function is positive or negative.

Process for finding the tangent of an angle using the sine and cosine values.

Method to find the reciprocal trigonometric functions (cosecant, secant, and cotangent) from sine, cosine, and tangent.

Explanation of coterminal angles and their impact on the trigonometric function values.

How to identify the angle's location on the unit circle and the associated signs for sine and cosine.

Use of the unit circle to find trigonometric values for angles greater than one full revolution.

Graphical representation of the unit circle and how it aids in understanding the periodic nature of trigonometric functions.

Practical approach to memorizing the unit circle and gradually moving towards solving problems without direct reference to it.

Techniques for dealing with negative angles and their corresponding trigonometric function values.

How to use a calculator to find trigonometric function values for angles not directly on the unit circle.

Emphasis on the importance of understanding why the unit circle works, rather than just memorizing the values.

Dealing with angles that are not a part of the standard set found on the unit circle using the properties of trigonometric functions.

The difference between degrees and radians in the context of the unit circle and how to switch between them on a calculator.

How to extend the concept of the unit circle to non-unit circles by using the radius to normalize the coordinates.

Transcripts

Browse More Related Video

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

An Indepth Look at Using Inverse Trig Functions (Precalculus - Trigonometry 21)

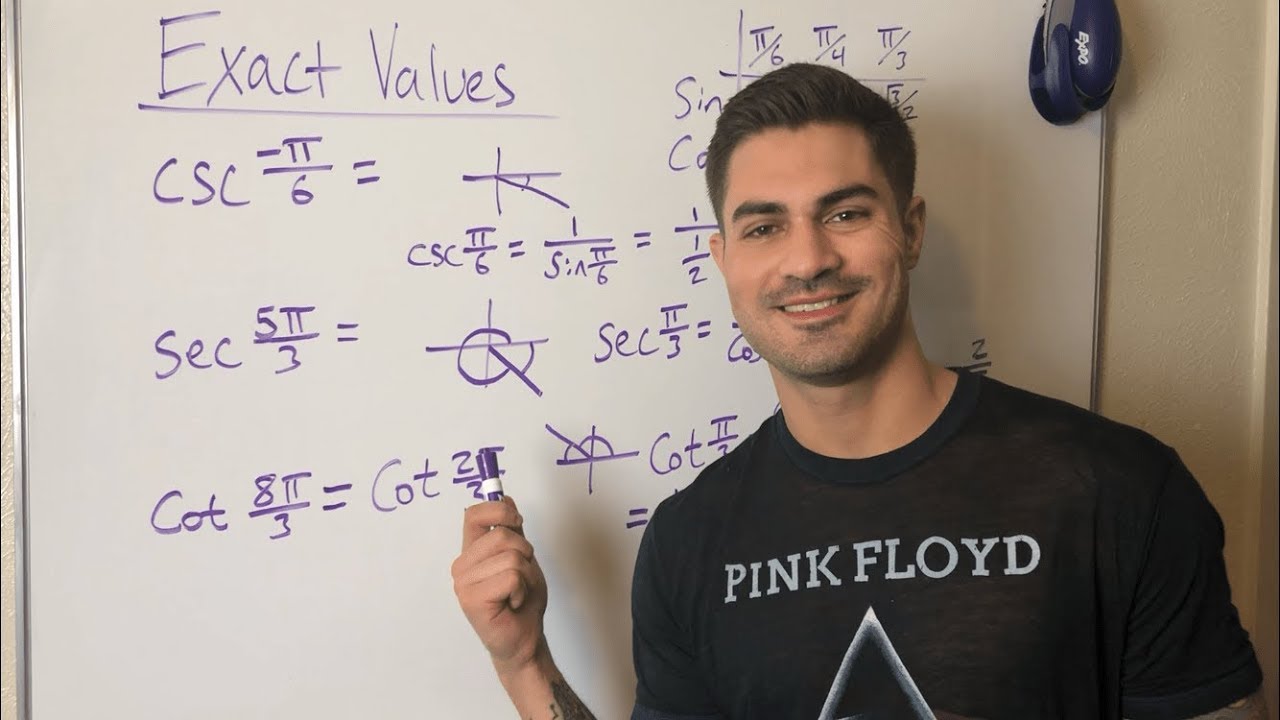
Finding Exact Values of Trig Functions

Basic Properties of Trigonometric Functions (Precalculus - Trigonometry 8)

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Related Tags

Unit Circle Trigonometry Sine Function Cosine Function Tangent Function Coterminal Angles Math Education Radian Measure Quadrant Analysis Trig Functions Reciprocal Identities