An Indepth Look at Using Inverse Trig Functions (Precalculus - Trigonometry 21)

Professor Leonard

26 Aug 202178:27

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the application of inverse trigonometric functions, such as arcsine, arccosine, arctangent, and their reciprocals like cosecant, secant, and cotangent. It emphasizes the importance of understanding the unit circle and the domains of these functions to accurately find angles based on given coordinates. The script provides a comprehensive guide on how to use inverse functions to map points on the unit circle to their corresponding angles, and vice versa, using the sine, cosine, and tangent functions. It also addresses the challenges of working with inverse functions outside the unit circle by constructing right triangles and applying the Pythagorean theorem. The video aims to clarify the process of finding angles for various trigonometric function values and the interplay between different trigonometric functions and their inverses, offering multiple examples to solidify the concepts.

Takeaways

📐 The unit circle is fundamental in understanding inverse trigonometric functions, as it helps to visualize the relationship between angles and their corresponding coordinates.
↔️ Inverse trigonometric functions reverse the process of regular trigonometric functions, taking a coordinate value and outputting the angle that creates that coordinate.
🚫 Domain restrictions are crucial for inverse trigonometric functions to work correctly, ensuring a one-to-one mapping between angles and coordinates.
🔄 Reciprocal relationships between sine and cosecant, and between cosine and secant, allow for the simplification of inverse functions by converting them into more familiar trigonometric functions.
🧭 The quadrant in which an angle lies is essential when working with inverse trigonometric functions, as it determines the sign of the coordinates and the appropriate function to use.
⌛ When an inverse trigonometric function does not directly yield an angle, drawing a right triangle and applying trigonometric relationships can help find the required angle.
🤔 Understanding the signs of coordinates in different quadrants is vital for determining the correct angle when working with inverse trigonometric functions.
🛠 The Pythagorean theorem is often used in conjunction with inverse trigonometric functions to find the missing sides of a right triangle when the angle is known.
📉 Asymptotes on the unit circle define the limits of the domains for the inverse trigonometric functions and must be considered when evaluating these functions.
🔢 Calculators can provide decimal approximations for angles when working with inverse trigonometric functions, but it's important to ensure the calculator is set to the correct mode (radians or degrees).
🤓 Mastery of inverse trigonometric functions comes from practice and understanding the underlying geometry and algebra, rather than relying solely on calculator tools.

Q & A

What is the main topic discussed in the video?
-The video discusses the use of inverse trigonometric functions, specifically sine, cosine, and tangent inverse, as well as the inverses of cosecant, secant, and cotangent.
What is the relationship between sine and its inverse function?
-The sine inverse function (also known as arcsine) takes a y-coordinate value from the unit circle and returns the angle (theta) that corresponds to that y-coordinate.
How does the domain of the sine function affect its inverse?
-The domain of the sine function is restricted to create a one-to-one function, which allows the inverse sine function to work effectively. This is done to avoid multiple angles having the same y-coordinate value.
What is the range of angles for which the sine inverse function is defined?
-The sine inverse function is defined for angles ranging from negative pi over two to pi over two (-π/2 to π/2).
How does the video demonstrate the process of finding the angle for sine inverse of a given value?
-The video uses the example of sine inverse of the square root of 2 over 2, showing that this value corresponds to the angle pi over four (π/4) on the unit circle.
What is the relationship between the tangent function and its inverse?
-The tangent inverse function (also known as arctangent) takes a y/x value and returns the angle that corresponds to that ratio, just as the tangent function takes an angle and returns the ratio of y to x.
Why is it necessary to consider the domain when working with inverse trigonometric functions?
-The domain is necessary to ensure that the inverse trigonometric function is one-to-one, meaning each output corresponds to a unique input, which is required for the inverse function to be valid.
How does the video approach the calculation of cosine of an angle found using an inverse trigonometric function?
-The video explains that once an angle is found using an inverse trigonometric function, the cosine of that angle can be calculated by recognizing that cosine takes an angle as input and provides an x-coordinate as output.
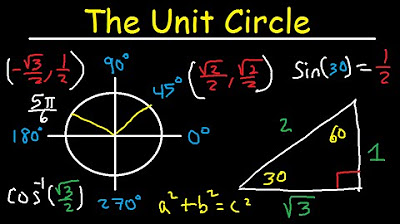
What is the significance of the unit circle in the context of inverse trigonometric functions?
-The unit circle is a visual tool used to find angles that correspond to given y or x coordinates when working with inverse trigonometric functions. It helps to visualize the relationship between angles and coordinates.
How does the video handle the calculation of the tangent of an angle found using the cosine inverse function?
-The video demonstrates that after finding the angle using the cosine inverse function, one can substitute this angle into the tangent function to find the corresponding y/x ratio, which is the tangent of the angle.
What is the process for finding the angle when dealing with the secant inverse function?
-The video explains that the secant inverse function will give an angle when provided with a y/x value. By finding the reciprocal of the y/x value and using the domain of the secant inverse function, one can find the corresponding angle.

Outlines

00:00

😀 Understanding Inverse Trigonometric Functions

This paragraph introduces the concept of inverse trigonometric functions, specifically arcsine, arccosine, and arctangent. It explains how these functions 'undo' the regular trigonometric functions to find the angle from a given coordinate on the unit circle. The importance of defining the domain for sine to create a one-to-one function is discussed, and the domains for sine, cosine, and tangent inverses are described.

05:00

🎓 Applying Inverse Functions to Find Angles

The paragraph demonstrates how to apply inverse trigonometric functions to find angles when given a coordinate. It uses the example of sine inverse of the square root of 2/2 to illustrate the process, emphasizing the need to consider the correct domain and how the unit circle can be used to find the angle that corresponds to a given y-coordinate.

10:01

🔢 Trigonometric Functions and Their Inverses

This section explores the relationship between regular trigonometric functions and their inverses. It explains how the outputs of inverse functions (angles) can be used as inputs for regular trigonometric functions. Examples include finding the cosine of an angle found using sine inverse and the tangent of an angle found using cosine inverse.

15:01

📐 Evaluating Inverse Trigonometric Functions with Coordinate Values

The paragraph focuses on evaluating inverse trigonometric functions when given specific coordinate values. It discusses the process of finding the angle that corresponds to a given x-coordinate for cosine inverse and a y-coordinate for sine inverse. The concept of using the unit circle to find these angles is emphasized.

20:02

🤔 Dealing with Inverse Trigonometric Functions Outside the Unit Circle

This part of the script addresses the challenge of dealing with inverse trigonometric functions when the context is outside the unit circle. It explains how to create a right triangle to find the necessary angle and then use that angle to evaluate the trigonometric function. The paragraph uses the example of sine of tangent inverse of one-half to illustrate this process.

25:03

🧮 Working with Inverse Trigonometric Functions and Their Reciprocals

The paragraph discusses the reciprocal relationships between certain trigonometric functions and their inverses, such as sine and cosecant, and how these relationships can be used to simplify the evaluation of inverse functions. It also explains the need to consider the domain of the functions when evaluating inverses and provides examples using cosecant and secant inverses.

30:04

📐 Using Pythagorean Theorem for Non-Unit Circle Inverse Functions

This section explains how to use the Pythagorean theorem to find the hypotenuse of a right triangle when dealing with inverse trigonometric functions that are not on the unit circle. It demonstrates how to find the angle that corresponds to a given y/x ratio by creating a triangle and using the Pythagorean theorem to find the missing side.

35:06

🔁 Finding Inverse Functions of Trigonometric Functions

The paragraph shows how to find the inverse functions of regular trigonometric functions. It emphasizes that these inverse functions will always be defined everywhere except where there is a vertical asymptote on the unit circle. The process involves finding the trigonometric function first and then restricting the domain to find the inverse.

40:06

🧲 Dealing with Cotangent Inverse Functions

This part of the script focuses on the special case of cotangent inverse functions, which do not match up well with the interval for tangent inverse functions. It explains how to deal with cotangent inverses by using the appropriate trigonometric function that overlaps in the same interval, such as cosine inverse, to find the angle.

45:14

🔍 Using Reciprocal Relationships for Inverse Trigonometric Functions

The final paragraph discusses the reciprocal relationships between cosecant and sine, and secant and cosine, which allows for a simplification when finding the inverse of these functions. It also provides an alternative method for finding the inverse of cosecant and secant functions using the sine and cosine inverses, respectively.

Mindmap

Keywords

💡Inverse Functions

Inverse functions are mathematical functions that 'reverse' another function. In the context of the video, inverse trigonometric functions such as arcsine, arccosine, and arctangent are discussed. These functions take a value from the range of the original trigonometric function and return an angle from the domain. They are used to find the angle that corresponds to a given trigonometric ratio, which is essential for understanding the relationship between angles and coordinates on the unit circle.

💡Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin of the coordinate plane. It is fundamental in the discussion of trigonometry as it provides a visual representation of the sine, cosine, and tangent of various angles. In the video, the unit circle is used to illustrate the values of trigonometric functions and how they relate to the angles, which is crucial for understanding inverse trigonometric functions.

💡Trigonometric Ratios

Trigonometric ratios, such as sine, cosine, and tangent, are the relationships between the angles of a right triangle and the lengths of its sides. In the video, these ratios are discussed in the context of the unit circle, where sine represents the y-coordinate, cosine the x-coordinate, and tangent the ratio of the y-coordinate to the x-coordinate of a point on the circle.

💡Domain and Range

In the context of functions, the domain refers to the set of all possible input values, while the range is the set of all possible output values. The video emphasizes the importance of understanding the domain and range of both trigonometric and inverse trigonometric functions, as they dictate the valid inputs and outputs for these functions and are crucial for finding correct angles and coordinates.

💡Reciprocal Trigonometric Functions

Reciprocal trigonometric functions are the cosecant, secant, and cotangent, which are the reciprocals of the sine, cosine, and tangent functions, respectively. The video explains how these functions can be used to find angles when given the ratios of the sides of a right triangle. They are particularly useful when dealing with inverse functions that correspond to the same domain as the original trigonometric functions.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry that states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. In the video, the theorem is used to find the hypotenuse of a right triangle when the other two sides are known, which is essential for working with non-unit circles and finding angles using trigonometric functions.

💡Rationalization

Rationalization is the process of simplifying a fraction by removing the radical (square root) from the denominator. In the video, rationalization is used when dealing with expressions involving square roots, ensuring that the final answer is in the simplest form and expressed as a fraction with a rational denominator. This technique is important for providing exact values for trigonometric functions and their inverses.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all angles and are fundamental in trigonometry. They include relationships like sine and cosine being squared and adding up to 1 (sin^2(x) + cos^2(x) = 1). In the video, identities are used to relate different trigonometric functions and their inverses, which helps in solving problems involving angles and coordinates on the unit circle.

💡Even and Odd Functions

Even functions are symmetric about the y-axis, and their values are the same for positive and negative inputs of the same absolute value, whereas odd functions are symmetric about the origin. In the video, the concept of even and odd functions is used to determine the values of cosine, which is an even function, and how it can be used to find angles in different quadrants.

💡Quadrants

Quadrants are the four equal parts of the Cartesian plane, each formed by the intersection of the x and y axes. In the video, quadrants are used to determine the signs of the x and y coordinates for different angles, which is essential for understanding the behavior of trigonometric functions and their inverses. The correct quadrant is crucial for finding the angle that corresponds to a given trigonometric ratio.

💡Calculator Usage

Calculators are used to find the values of trigonometric functions and their inverses, especially when dealing with non-unit circles or complex values. In the video, the presenter discusses how to use a calculator to find angles for cotangent inverse and other inverse trigonometric functions, emphasizing the importance of setting the calculator to the correct mode (radians or degrees) for accurate results.

Highlights

Introduction to inverse trigonometric functions: sine inverse, cosine inverse, tangent inverse, and their applications.

Explanation of how inverse functions reverse the process of normal trigonometric functions to find angles from coordinates.

The importance of domain and range in ensuring a one-to-one function for inverse trigonometric functions to work correctly.

Use of the unit circle to find angles for sine, cosine, and tangent inverse functions within specific quadrants.

Procedure to find the angle for sine inverse of a given y-coordinate, such as sine inverse of square root of 2 over 2.

Understanding that the outputs of inverse trigonometric functions are angles, which can then be used as inputs for regular trigonometric functions.

Method to find cosine of an angle derived from cosine inverse, such as cosine of pi over 4.

Approach to deal with tangent inverse when the function is not defined on a unit circle by creating a right triangle.

Technique to find the angle for cotangent inverse that does not correspond to a unit circle using a triangle and cosine inverse.

Explanation of how to handle secant inverse and cosecant inverse by utilizing their corresponding trigonometric functions due to matching domains.

Process to find the angle for trigonometric functions when the radius of the circle is not one, using the Pythagorean theorem.

Use of reciprocal relationships between sine and cosecant, and cosine and secant, to simplify the process of finding inverse functions.

Handling of cotangent inverse by recognizing its different domain and using the appropriate trigonometric function based on the quadrant.

Strategy to find angles for inverse trigonometric functions when they do not correspond to a unit circle using calculator functions.

Emphasis on the importance of understanding the unit circle and the domains of trigonometric functions for solving inverse functions.

Illustration of how to find the angle for sine inverse and use it to calculate the sine of that angle, even without knowing the angle's exact value.

Comprehensive examples demonstrating the process of finding angles from inverse trigonometric functions and then evaluating the original trigonometric functions.

Transcripts

Browse More Related Video

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

How to Use the Unit Circle in Trigonometry (Precalculus - Trigonometry 7)

Basic Properties of Trigonometric Functions (Precalculus - Trigonometry 8)

Trigonometry: Unit Circle

Unit Circle Trigonometry - Sin Cos Tan - Radians & Degrees

Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)

Related Tags

Inverse Trigonometry Unit Circle Trig Functions Angle Calculation Math Tutorial Sine Cosine Tangent Cosecant Secant Cotangent Domain Restrictions Pythagorean Theorem Trigonometric Identities