PreCalculus - Matrices & Matrix Applications (5 of 33) Method of Gaussian Elimination: Example

Michel van Biezen
8 Jun 201509:54
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step guide on using the Gaussian elimination method to solve a system of linear equations represented by a matrix. It explains how to transform the augmented matrix into row echelon form and then to reduced row echelon form, ultimately allowing the determination of the values for variables x, y, and z. The process involves a series of row operations, including multiplication and addition, to achieve a diagonal of ones and zeros elsewhere, leading to a clear solution for the system.

Takeaways
  • 📌 The Gaussian method of elimination is used to find the row echelon or reduced row echelon form of a matrix representing a system of linear equations.
  • 🔢 The process starts by transforming the top-left element of the matrix into a 1, typically by dividing the entire row by the element's value.
  • ↕️ To eliminate unwanted values below the leading 1, rows are manipulated by adding or subtracting multiples of other rows.
  • 🔄 For the reduced row echelon form, zeros are achieved in all positions not on the diagonal, meaning every diagonal element should be 1.
  • 🎯 The goal of the process is to simplify the system of equations to a point where the values of x, y, and z (if present) can be directly read from the matrix.
  • 📈 The augmented matrix is used to represent the system of equations, with the coefficients and constants laid out in an organized manner.
  • 🚶‍♂️ The process involves a series of steps: getting the leading 1, eliminating values below it, and then moving to the next diagonal element.
  • 🔢 Each row operation is a systematic approach to achieve the desired form, with each step building upon the previous one.
  • 🔄 The final result is a matrix that allows for easy extraction of the solutions for the variables involved in the system of equations.
  • 📚 The method is a powerful tool for solving systems of linear equations, offering an alternative to algebraic manipulation.
  • 📈 The Gaussian elimination method is widely applicable and can be used for systems with more variables and more complex matrices.
Q & A

  • What is the Gaussian method of elimination used for?

    -The Gaussian method of elimination is used for solving a system of linear equations by transforming the augmented matrix representing the system into row echelon form or reduced row echelon form.

  • How does one start the Gaussian elimination process?

    -The process starts by focusing on the upper left corner element of the matrix. The first step is to make this element equal to 1 by dividing the entire row by the value of that element.

  • What is an augmented matrix?

    -An augmented matrix is a matrix that combines the coefficients of a system of linear equations and their constants in one large matrix, allowing for the application of row operations to solve the system.

  • How does one eliminate unwanted values from a row?

    -To eliminate unwanted values, one can use the rows with desired values (like 1s) and perform row operations such as multiplying by the required constants and adding or subtracting them from the row with the unwanted values.

  • What is the goal of transforming the matrix into row echelon form?

    -The goal is to have 1s down the main diagonal and zeros elsewhere, which allows for a simpler solution to the system of linear equations by directly reading the values of the variables from the matrix.

  • What is the difference between row echelon form and reduced row echelon form?

    -In the row echelon form, the goal is to have 1s down the diagonal and zeros in the lower left corner. In the reduced row echelon form, not only 1s are on the diagonal, but also all the other elements in each column (except the pivot positions) are zeros.

  • How can one find the values of the variables x, y, and z from the transformed matrix?

    -Once the matrix is in row echelon or reduced row echelon form, one can read the values of the variables directly from the columns. The column corresponding to a variable will have its value (non-zero) at the pivot position, and 0s elsewhere for the reduced row echelon form.

  • What happens when the final matrix has all zeros in the last row?

    -If the final matrix has all zeros in the last row, it means there is no unique solution to the system of equations, and the system is underdetermined or inconsistent.

  • How does one solve for additional variables in an extended system?

    -To solve for additional variables, one would continue the Gaussian elimination process, applying the same row operations to achieve the desired form for each additional variable in the system.

  • What is the significance of the pivot position in the matrix?

    -The pivot position is the first non-zero entry in each row from the left. It is the leading entry used for subsequent row operations to achieve the row echelon or reduced row echelon form.

  • How can one verify the solution of a system of linear equations?

    -The solution can be verified by substituting the found values of the variables back into the original equations to check if all the equations hold true. If they do, the solution is correct.

  • What are the steps to reduce a matrix to its reduced row echelon form?

    -The steps include getting 1s on the diagonal through appropriate row multiplication, eliminating non-pivot elements by row addition or subtraction, and finally, normalizing the diagonal elements to 1 by dividing the corresponding rows by the pivot values. Additional row operations are performed to ensure all non-pivot columns have zeros.

Outlines
00:00
📊 Gaussian Method of Elimination

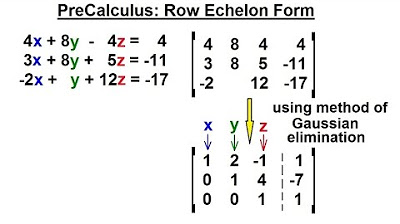
The paragraph introduces the Gaussian method of elimination, a technique used to find the row echelon or reduced row echelon form of a matrix. This matrix represents a system of three linear equations, with the goal of finding values for x, y, and z that satisfy all equations. The process begins by transforming the augmented matrix to have ones across the diagonal and zeros elsewhere. The first step involves making the top-left element a 1 by dividing the entire row by the element's value. The subsequent steps involve using rows with 1s to eliminate all other elements in the same column, resulting in a matrix where the second row has a 1 and the third row has zeros in the first two columns. The explanation is clear and methodical, providing a step-by-step guide on how to achieve the desired matrix form.

05:02
🔄 Achieving Row Echelon and Reduced Row Echelon Forms

This paragraph continues the explanation of the Gaussian elimination method, focusing on achieving the row echelon and reduced row echelon forms of the matrix. The process involves further manipulation of the matrix to get zeros in the appropriate places and ones along the diagonal. The explanation details how to divide rows to get a 1, use negative multipliers to replace rows to achieve zeros, and finally, adjust the last row to get the desired form. The paragraph concludes with the solution to the system of equations, showing how the final matrix form can be used to directly read off the values of x, y, and z. The explanation emphasizes the preference for the reduced row echelon form and the potential for further examples to illustrate the method with different systems of linear equations.

Mindmap
Keywords
💡Gaussian method of elimination
The Gaussian method of elimination, also known as Gaussian elimination, is a systematic procedure used to solve systems of linear equations by transforming the augmented matrix representing these equations into a row echelon form or reduced row echelon form. This method involves a series of row operations such as swapping rows, multiplying a row by a non-zero scalar, and adding or subtracting one row from another. In the context of the video, this method is used to find the values of x, y, and z that satisfy a given system of three linear equations.
💡Row echelon form
Row echelon form is a specific layout of a matrix where the following conditions are met: there are no zeros in the main diagonal, and every element above the main diagonal is zero. This form is an intermediate step in the process of solving systems of linear equations using the Gaussian elimination method. The video script describes the process of transforming the augmented matrix into this form to simplify the system of equations and make it easier to read off the solution.
💡Reduced row echelon form
Reduced row echelon form is a special type of matrix form that goes a step further than the row echelon form by ensuring that all the leading entries (the entries in the main diagonal) are 1s, and all the entries below these leading entries are zeros. This form makes it very easy to interpret the solutions of the system of linear equations, as each column corresponding to a leading entry represents a variable that can be solved for directly. In the video, the presenter aims to achieve this form to clearly identify the values of x, y, and z.
💡Augmented matrix
An augmented matrix is a matrix that combines the coefficients of a system of linear equations with the constants from the right-hand side of the equations. It is used as a visual tool in the process of solving these systems, particularly when employing methods like Gaussian elimination. The video script describes how to manipulate an augmented matrix to find the solution to the system of equations it represents.
💡Linear equations
Linear equations are mathematical equations in which the highest power of the variables is one. They represent straight lines in two-dimensional space and planes in three-dimensional space. Solving systems of linear equations involves finding the values of the variables that satisfy all equations simultaneously. The video script focuses on using the Gaussian elimination method to solve such systems.
💡Diagonal
In the context of matrices, the diagonal refers to the set of cells that run from the top left corner to the bottom right corner. For example, in a 3x3 matrix, the diagonal would include the cells in the first row and first column, the second row and second column, and so on. In the video, the process of achieving row echelon and reduced row echelon forms involves manipulating the matrix so that there are ones on the diagonal and zeros in the positions immediately below these ones.
💡Row operations
Row operations are the fundamental steps used in Gaussian elimination to transform the matrix. These include swapping two rows, multiplying a row by a non-zero scalar, and adding or subtracting a multiple of one row to another row. These operations are reversible and do not change the solution set of the system of linear equations. The video script provides a detailed explanation of how to perform these operations to achieve the desired matrix forms.
💡Variables
In the context of linear equations, variables are symbols, often represented by letters such as x, y, and z, that stand for unknown quantities. The goal of solving a system of linear equations is to find the values of these variables that satisfy all the equations simultaneously. The video script is focused on finding the values of variables x, y, and z for a given system of three equations.
💡Solution
In mathematics, a solution to a system of linear equations is the set of values for the variables that make all the equations true simultaneously. The process of solving the system involves using methods like Gaussian elimination to manipulate the equations until the solution becomes clear. The video script describes how to arrive at the solution by transforming the augmented matrix into reduced row echelon form, which directly reveals the values of the variables.
💡Systems of linear equations
A system of linear equations is a collection of multiple linear equations that are considered simultaneously. These systems can be used to model a wide variety of real-world situations involving relationships between different quantities. The video script is focused on the process of solving such systems using the Gaussian elimination method and the concept of augmented matrices.
Highlights

Introduction to the Gaussian method of elimination for solving systems of linear equations.

Use of an Augmented matrix to represent the system of equations.

The goal of transforming the matrix into row echelon form or reduced row echelon form.

Process of making the first element in the upper left corner a 1 by row multiplication.

Elimination of unwanted elements below the pivot position using row operations.

Technique for zeroing elements in the second column by subtracting multiples of row 1 from row 2 and row 3.

Transforming the second element in the pivot position to 1 by dividing the row by 2.

Elimination of the 5 in the third row by subtracting multiples of row 2 from row 3.

Adjusting the third row to achieve a 1 in the final pivot position by dividing by the pivot element.

Conversion of the row echelon form to the reduced row echelon form for a simplified solution.

Deriving the solution of the system of linear equations by back substitution from the row echelon form.

Explanation of how to read the values of x, y, and z from the reduced matrix.

Demonstration of the Gaussian elimination process on a system of equations with unique solutions.

Emphasis on the practical application of Gaussian elimination for solving complex systems of linear equations.

Transcripts

Browse More Related Video

Gaussian Elimination & Row Echelon Form

Gaussian Elimination With 4 Variables Using Elementary Row Operations With Matrices

PreCalculus - Matrices & Matrix Applications (10 of 33) Gaussian Elimination: Example of Solving 3x3

PreCalculus - Matrices & Matrix Applications (7 of 33) Method of Gaussian Elimination: 3x3 Matrix*

7.3.4 Reduced Row Echelon Form

PreCalculus - Matrices & Matrix Applications (3 of 33) Row Echelon Form

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
LinearAlgebraGaussianEliminationMatrixTransformationRowEchelonFormMathematicsEducationalContentProblemSolvingAlgorithmicProcessMathTutorialsAbstractAlgebra