7.3.2 Gaussian Elimination
TLDRThis video tutorial, led by Mr. Mack Wilberg, delves into the method of Gaussian elimination for solving systems of linear equations. The process involves transforming the system into row echelon form using three key operations: interchanging equations, multiplying/dividing by non-zero constants, and adding multiples of equations. The video demonstrates step-by-step how to apply these operations to a given system, ultimately aiming for a top equation that leads with a variable 'X', a second with 'Y', and a third with 'Z'. The method simplifies the system, allowing for easier solution through back substitution. However, the video also highlights a scenario where the system has no solution, indicated by a mathematically nonsensical statement, emphasizing the importance of careful calculation and verification of results throughout the process.
Takeaways
- 📚 Gaussian elimination is a method for solving systems of linear equations by transforming them into row echelon form.
- 🔄 The three operations used in Gaussian elimination are: interchanging equations, multiplying/dividing by a nonzero constant, and adding/subtracting multiples of equations.
- 🛤️ The goal of row echelon form is to create a stair-step pattern where each leading variable (x, y, z, etc.) is progressively isolated.
- 🔢 The first equation should be simplified to lead with a variable x, the second with y (without x), and the third with z (without x and y).
- 📈 To eliminate a variable, multiply the equation by the necessary factor to create a coefficient of the opposite sign, then add/subtract it from the target equation.
- 🚫 Care must be taken to avoid reintroducing variables that have been previously eliminated.
- 🔎 When performing Gaussian elimination, it is crucial to be cautious with signs and arithmetic to prevent mistakes.
- 🔄 The process can be checked by substituting the found values back into the original equations to ensure they satisfy all equations.
- ⚠️ If during the process a row leads to 0 = a nonzero number, it indicates that the system has no solution.
- 📝 The final result can be expressed as an ordered triple (x, y, z) representing the values of the variables that satisfy all equations in the system.
Q & A
What is Gaussian elimination?
-Gaussian elimination is a process used to transform a system of linear equations into row echelon form, making it easier to solve by systematically eliminating variables.
What are the three operations used in Gaussian elimination?
-The three operations are: 1) Interchanging any two equations, 2) Multiplying or dividing an equation by a nonzero constant, and 3) Adding a multiple of one equation to another equation.
What is the goal of transforming a system of equations into row echelon form?
-The goal is to arrange the system in a stair-step pattern where each equation leads off with a different variable (X, then Y, then Z), allowing for easier solution of the system.
How does the speaker plan to start building the new system in the example given?
-The speaker plans to start by rearranging the equations so that the one leading with a plane X (X - 2y + Z = 7) is at the top of the new system.
What mistake should one avoid when performing Gaussian elimination?
-One should avoid making mistakes with negative signs during the process and ensure correct addition when performing the elimination steps.
How does the speaker eliminate the X's from the second equation in the example?
-The speaker multiplies the middle equation by -3 and adds it to the top equation, which results in the cancellation of the X's and leads to an equation with just Y and Z.
What does the speaker do after getting the system into row echelon form?
-After getting the system into row echelon form, the speaker uses back substitution to find the values of the variables X, Y, and Z.
How does the speaker check the solution of the system?
-The speaker suggests plugging the found values of X, Y, and Z back into the original equations to ensure they satisfy all three equations.
What does it mean when you get a statement that doesn't make mathematical sense in the process?
-If you get a statement that doesn't make mathematical sense, like 0 = 2, it indicates that the system of equations has no solution.
What is the significance of the stair-step pattern in row echelon form?
-The stair-step pattern in row echelon form is significant because it progressively eliminates variables from each equation, starting with the top and working downwards, which simplifies the process of finding the solution.
Outlines
📚 Introduction to Gaussian Elimination
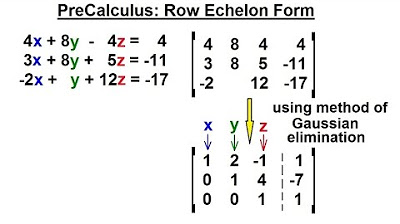
This paragraph introduces the concept of Gaussian elimination, a method used to solve a system of linear equations by transforming them into row echelon form. The process involves three key operations: interchanging equations, multiplying/ dividing by a non-zero constant, and adding multiples of one equation to another. The goal is to arrange the equations in a way that progressively eliminates variables, starting with the top equation leading with a variable x, followed by an equation leading with y without x, and finally an equation leading with z without x or y. The example provided demonstrates the initial steps of Gaussian elimination to set up the system for easier solution.
🔢 Elimination and Row Echelon Form
In this paragraph, the focus is on the elimination process within Gaussian elimination. The speaker explains how to use the rules to eliminate variables from the equations, specifically targeting the x's and y's in the given system. Through a series of operations, including multiplication by negative numbers and addition of equations, the system is gradually transformed. The speaker emphasizes the importance of careful calculation and the potential for mistakes. The process results in a row echelon form where the last equation allows for the determination of the variable z, with the values of x and y to be found using back substitution.
❌ Identifying No Solution Scenario
The final paragraph discusses a scenario where the system of equations has no solution. This is identified when an impossible equation arises during the elimination process, such as zero not being equal to a non-zero number. The speaker illustrates this by attempting to eliminate x's from the last equation and inadvertently creating a contradiction. The paragraph emphasizes the importance of checking the results and the fact that a nonsensical mathematical statement indicates an inconsistency in the system, leading to the conclusion that there is no solution.
Mindmap
Keywords
💡Gaussian Elimination
💡Row Echelon Form
💡Linear Equations
💡Interchange Rows
💡Multiply or Divide by Nonzero Constant
💡Add Multiple of One Equation to Another
💡Variables
💡Stair-step Pattern
💡Back Substitution
💡No Solution
Highlights
Gaussian elimination is a process used to transform a system of linear equations into row echelon form.
Three operations can be used in Gaussian elimination: interchanging equations, multiplying/dividing by nonzero constants, and adding multiples of equations.
The goal of row echelon form is to gradually eliminate variables, leading with a plane X in the top equation, then Y in the second, and finally Z in the last.
The first step in the example is to rearrange equations so that the top equation leads with a plane X.
To eliminate X terms from the second equation, multiply the leading X equation by the necessary constant and add it to the equation with X terms.
When performing Gaussian elimination, it's crucial to be careful with negative signs and addition to avoid mistakes.
After transforming the system into row echelon form, back substitution can be used to find the values of the variables.
The example demonstrates how to find the value of Z by eliminating X and Y terms from the bottom equation.
Once the values of X, Y, and Z are found, they can be written as an ordered triple to represent the solution.
The transcript also shows an example where the system has no solution due to a mathematical contradiction.
In the no-solution example, the contradiction arises when zero is found to equal two after the elimination process.
The video emphasizes the importance of checking answers and verifying that the solution satisfies all original equations.
The process of Gaussian elimination is demonstrated step by step, showing how to handle different scenarios in solving systems of linear equations.
The transcript provides a clear and detailed explanation of Gaussian elimination, making it accessible for learners to understand and apply.
The example of no solution highlights the importance of logical consistency in mathematical problem-solving.
The transcript is a valuable resource for those learning about linear algebra and the techniques for solving systems of linear equations.
The method of Gaussian elimination is showcased as a powerful tool for solving complex systems of linear equations.
The video concludes by reinforcing the key concepts of Gaussian elimination and its application in solving systems of linear equations.
Transcripts
Browse More Related Video

PreCalculus - Matrices & Matrix Applications (7 of 33) Method of Gaussian Elimination: 3x3 Matrix*

Gaussian Elimination With 4 Variables Using Elementary Row Operations With Matrices

Gaussian Elimination & Row Echelon Form

PreCalculus - Matrices & Matrix Applications (5 of 33) Method of Gaussian Elimination: Example
PreCalculus - Matrices & Matrix Applications (3 of 33) Row Echelon Form

Gauss Jordan Elimination & Reduced Row Echelon Form
5.0 / 5 (0 votes)
Thanks for rating: