Related Rates - Gravel Dumped Into Conical Tank Problem
TLDRThe transcript describes two related rates problems involving cones. The first problem calculates the rate of change of the height of a conical pile of gravel, given the volume rate and the relationship between the base diameter and height. The second problem determines the rate of water flow into an inverted conical tank, considering the rate of water leakage and the dimensions of the tank. Both problems use mathematical modeling and differentiation to find the rates, resulting in 1/(18π) feet per minute for the gravel pile's height increase and 3358 cubic centimeters per minute for the water flow into the tank.
Takeaways
- 📏 The problem involves a conical pile of gravel formed by a conveyor belt, with the rate of volume increase being 50 cubic feet per minute.
- 🔄 The diameter of the base of the cone is always five times the height of the pile, providing a relationship between the dimensions of the cone.
- 📈 The goal is to find the rate at which the height of the pile is increasing when the pile is 12 feet high.
- 🔢 The volume of a cone is given by the formula (1/3)πr²h, which is used to relate the volume change to the dimensions of the cone.
- 📚 The problem requires differentiating the volume equation with respect to time to find the rate of change of the height (dh/dt).
- 🔧 The relationship between the radius (r) and height (h) of the cone is used to eliminate one variable and solve for the other.
- 🧮 When h is 12 feet, the calculation yields a rate of increase for the height (dh/dt) of 1/(18π) feet per minute.
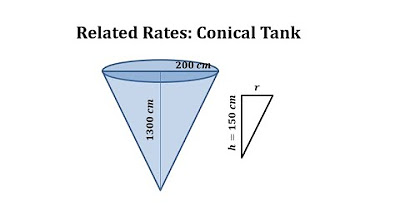
- 💧 The second problem involves an inverted conical tank with water leaking out at a rate of 7,500 cubic centimeters per minute.
- 🏺 The height of the water in the tank is 0.25 meters, and the rate at which the water level is falling is 15 centimeters per minute.
- 🔄 The task is to find the rate at which water is flowing into the tank, considering both the inflow and outflow.
- 📈 The volume change equation for the tank is adapted to account for the falling water level, with the radius (r) expressed in terms of the height (h).
- 🧮 By solving the net volume flow rate equation, the rate at which water is flowing into the tank is found to be 3,358 cubic centimeters per minute.
Q & A
What is the rate at which gravel is falling off the conveyor belt?
-The gravel is falling off the conveyor belt at a rate of 50 cubic feet per minute.
What is the relationship between the diameter and the height of the conical pile?
-The diameter of the base of the cone is always five times the height of the pile.
How is the volume of a cone calculated?
-The volume of a cone is calculated using the formula 1/3 * pi * r^2 * h, where r is the radius of the base and h is the height of the cone.
What is the goal of the first problem in the script?
-The goal of the first problem is to determine the rate at which the height of the conical pile is changing when the pile is 12 feet high.
How is the derivative of the volume of the cone with respect to time (dv/dt) related to the derivative of the height with respect to time (dh/dt)?
-The derivative of the volume of the cone with respect to time is related to the derivative of the height with respect to time through the equation 50 = (25/12) * pi * (h^3) * (dh/dt).
What is the rate at which water is leaking out of the inverted conical tank?
-The water is leaking out of the inverted conical tank at a rate of 7,500 cubic centimeters per minute.
What is the height and diameter of the conical tank when the water level is falling at a rate of 15 centimeters per minute?
-When the water level is falling at a rate of 15 centimeters per minute, the height of the water in the tank is 0.25 meters (or 25 centimeters), and the diameter at the top is 6 meters.
How can we find the rate at which water is flowing into the tank?
-We can find the rate at which water is flowing into the tank by calculating the net volume flow rate, which is the difference between the rate of water flowing into the tank and the rate of water flowing out of the tank.
What is the final calculated rate at which water is flowing into the tank?
-The final calculated rate at which water is flowing into the tank is 3,358 cubic centimeters per minute.
Why is the rate of water flowing into the tank positive?
-The rate of water flowing into the tank is positive because this quantity represents the increase in the volume of water in the tank, whereas the leaking water decreases the volume.
How is the height of the cone related to the radius in the second problem?
-In the second problem, the height of the cone is related to the radius by the ratio 8d = 6h, which leads to r being equal to 3h/8.
What units were used in the calculations for the second problem?
-In the second problem, the units used were meters and centimeters, with the final answer being in cubic centimeters per minute.
Outlines
📈 Calculating the Rate of Increase of a Conical Pile's Height
This paragraph discusses a related rates problem involving a conical pile formed by gravel falling off a conveyor belt at a rate of 50 cubic feet per minute. The base diameter of the cone is always five times the height of the pile. The goal is to determine the rate at which the height of the pile is increasing when the pile is 12 feet high. The solution involves understanding the volume of a cone, which is given by the formula (1/3)πr^2h, and differentiating this with respect to time to find the rate of change of height (dh/dt). The relationship between the diameter and height (d = 5h) is used to eliminate the radius variable, leading to the equation 50 = (25π/12)(dh/dt). Solving this, the rate of increase of the height is found to be 1/(18π) feet per minute.
💧 Determining the Rate of Water Flow into a Leaky Conical Tank
The second paragraph presents a problem where water is leaking out of an inverted conical tank at a rate of 7,500 cubic centimeters per minute, and the tank has a height of eight meters with a top diameter of six meters. The water level is falling at a rate of 15 centimeters per minute when the height of the water is 0.25 meters. The task is to find the rate at which water is flowing into the tank. The solution requires understanding the net volume flow rate, which is the difference between the rate of water flowing into and out of the tank. The volume of the cone is given by (1/3)πr^2h, and by substituting the known values and solving the equation, the net rate of change of volume (dv/dt) is calculated. By adding the rate of water flowing out (7,500 cm³/min) to the net change in volume, the rate of water flowing into the tank (3,358 cm³/min) is determined.
Mindmap
Keywords
💡related rates problem
💡conveyor belt
💡circular base
💡volume
💡differentiation
💡height of the pile
💡diameter
💡radius
💡rate of change
💡cubic feet
💡inverted conical tank
Highlights
Gravel falls off a conveyor belt onto a conical pile at a rate of 50 cubic feet per minute.
The diameter of the base of the cone is always five times the height of the pile.
The problem aims to determine how fast the height of the pile is increasing when the pile is 12 feet high.
The volume of a cone is represented by the equation 1/3 * pi * r^2 * h.
To find the rate of change of height (dh/dt), we relate the height to the volume with dv/dt = 50 cubic feet per minute.
The relationship between the radius (r) and height (h) is r = 5/2 * h.
Differentiating the volume equation with respect to time gives us the equation involving dr/dt and dh/dt.
The final calculation for the rate at which the height is changing (dh/dt) is 1/(18 * pi) feet per minute when the pile is 12 feet high.
The second problem involves water leaking out of an inverted conical tank at a rate of 7,500 cubic centimeters per minute.
The height of the tank is eight meters, and it has a diameter of six meters at the top.
The water level is falling at a rate of 15 centimeters per minute when the height of the water is 0.25 meters.
The goal is to find the rate at which water is flowing into the tank.
The net volume flow rate is the difference between the rate of water flowing into and out of the tank.
The volume of a cone is given by the equation 1/3 * pi * r^2 * h, which is used to calculate the net rate of volume change.
The relationship between the height (h) and radius (r) of the tank is r = 3h/8.
The derivative of the volume equation with respect to time (t) gives us the net dv/dt.
The net volume flow rate (dv/dt) is -4142 cubic centimeters per minute, indicating the rate at which the water level is decreasing.
To find the rate at which water is flowing into the tank (dv/dt), we add 7,500 cubic centimeters per minute to the net volume flow rate.
The final answer for the rate at which water is flowing into the tank is 3,358 cubic centimeters per minute, which is positive because it increases the volume of water.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: