The Speed, Distance and Time trick [No Ads]

Xcelerate Math
4 Jul 201905:00
EducationalLearning
32 Likes 10 Comments

TLDRIn this Xcelerate Maths lesson, the fundamental rules of speed, distance, and time are explored and applied to real-life scenarios. The DST triangle mnemonic is introduced to help remember the formulas: distance equals speed times time, speed equals distance divided by time, and time equals distance divided by speed. The lesson includes examples involving a car, an express train, a snail, a snake's attack, and a rocket trip from Earth to the Moon, illustrating how these rules can be used to solve various problems.

Takeaways
  • 📐 The lesson introduces the fundamental rules of speed, distance, and time, and their practical applications in real life.
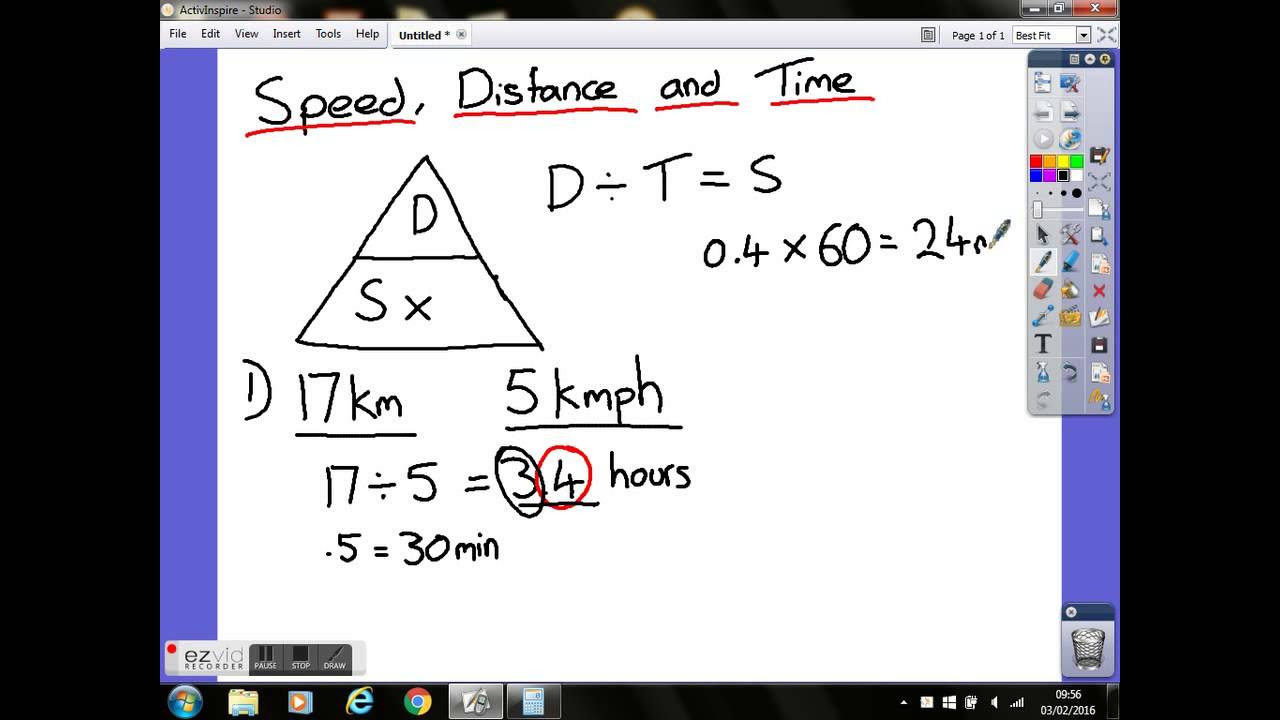
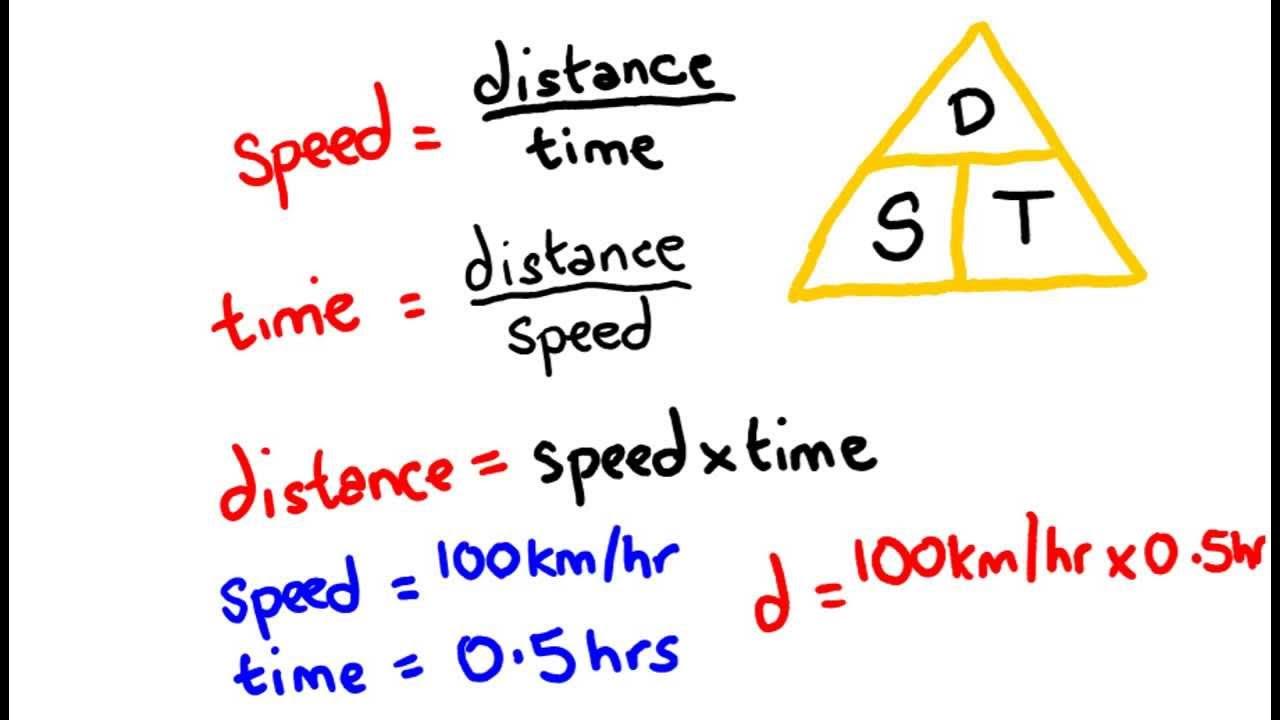
  • 🔤 The DST triangle is a mnemonic tool to remember the relationships between distance (D), speed (S), and time (T), with the letters in alphabetical order.
  • 🚀 The distance rule is derived by multiplying speed by time, represented as Distance = Speed × Time.
  • 🛤️ The speed rule is found by dividing distance by time, which is expressed as Speed = Distance ÷ Time.
  • ⏳ To find time, the rule is to divide distance by speed, as Time = Distance ÷ Speed.
  • 🚗 A practical example is given where a car travels 100 km/h for 4 hours, covering a distance of 400 km.
  • 🚄 Another example involves an express train that travels 1500 km in 3 hours, with a speed of 500 km/h.
  • 🐌 A snail's pace is calculated by dividing the distance it travels (80 mm) by its speed (10 mm/s), resulting in 8 seconds.
  • 🐍 A challenge question about a snake's speed is solved by finding it attacks at 15 m/s when 3 m away in 0.2 seconds.
  • 🚀 A final challenge calculates the time it takes for a rocket to travel from Earth to the Moon, which is 15.25 hours at a speed of 7 km/s over a distance of 384,000 km.
  • 📝 The script emphasizes the importance of understanding these rules for problem-solving in various contexts.
Q & A

  • What are the three rules in the DST triangle and how are they represented?

    -The three rules in the DST triangle represent the relationships between distance (D), speed (S), and time (T). The distance rule is represented as Distance = Speed × Time. The speed rule is represented as Speed = Distance ÷ Time. And the time rule is represented as Time = Distance ÷ Speed. These rules help in solving various real-life problems involving motion.

  • How can the DST triangle be used to derive the formula for distance?

    -The DST triangle can be used to derive the distance formula by highlighting the 'D' in the triangle. Since 'S' and 'T' are alongside each other, we multiply them to get the formula for distance, which is Distance = Speed × Time.

  • What is the formula for speed according to the DST triangle?

    -According to the DST triangle, the formula for speed is derived by highlighting the 'S' in the triangle, with 'D' being above 'T'. This gives us the formula Speed = Distance ÷ Time.

  • How can we find the time taken to cover a certain distance using the DST triangle?

    -To find the time taken to cover a certain distance, we use the 'T' in the DST triangle, with 'D' being above 'S'. This leads to the formula Time = Distance ÷ Speed, which can be used to calculate the time taken.

  • If a car travels at a speed of 100 km/h for 4 hours, how far does it travel?

    -Using the distance formula from the DST triangle (Distance = Speed × Time), a car traveling at 100 km/h for 4 hours will cover a distance of 400 km (100 km/h × 4 h = 400 km).

  • How fast does an express train travel if it covers a distance of 1500 km in 3 hours?

    -Using the speed formula from the DST triangle (Speed = Distance ÷ Time), an express train that covers 1500 km in 3 hours travels at a speed of 500 km/h (1500 km ÷ 3 h = 500 km/h).

  • How long does it take for a snail to move 80 mm at a speed of 10 mm/s?

    -Using the time formula from the DST triangle (Time = Distance ÷ Speed), it takes a snail 8 seconds to move 80 mm at a speed of 10 mm/s (80 mm ÷ 10 mm/s = 8 s).

  • What is the speed of a snake that can attack in 0.2 seconds if the distance to the target is 3 m?

    -Using the speed formula (Speed = Distance ÷ Time), the snake's speed is 15 m/s, given that it covers a distance of 3 m in 0.2 seconds (3 m ÷ 0.2 s = 15 m/s).

  • How long would it take for a rocket to travel from the earth to the moon if the distance is 384,000 km and the rocket travels at a constant speed of 7 km/s?

    -Using the time formula (Time = Distance ÷ Speed), the journey time for the rocket would be 54,914 seconds (384,000 km ÷ 7 km/s = 54,914 s). Converting this to minutes and then to hours, the final answer is 15.25 hours for the rocket to travel from the earth to the moon.

  • What is the significance of the DST triangle in solving motion-related problems?

    -The DST triangle is a mnemonic tool that helps in remembering the relationships between distance, speed, and time. It provides a structured way to approach problems involving motion, making it easier to identify the known values and apply the correct formula to find the unknown quantity.

  • How do you convert the time taken for the rocket to travel from the earth to the moon from seconds to hours?

    -To convert the time from seconds to hours, you first divide the number of seconds by 60 to get the minutes (54,914 s ÷ 60 = 915.23 minutes). Then, you divide the number of minutes by 60 again to get the hours (915.23 min ÷ 60 ≈ 15.2555 hours). Rounding this to two decimal places gives us approximately 15.25 hours.

  • What is the practical application of understanding the relationship between speed, distance, and time?

    -Understanding the relationship between speed, distance, and time is crucial in various real-life scenarios such as calculating travel durations, designing transportation systems, analyzing sports performance, and even in emergency response times. It helps in planning and decision-making processes by providing a clear picture of how long it takes to cover certain distances at given speeds.

Outlines
00:00
📚 Introduction to Speed, Distance, and Time Concepts

This paragraph introduces the viewers to the fundamental concepts of speed, distance, and time in the context of Xcelerate Maths. It explains the use of a DST triangle as a mnemonic device to remember the three rules: distance equals speed multiplied by time, speed equals distance divided by time, and time equals distance divided by speed. The paragraph also provides real-life examples to demonstrate how to apply these rules, such as calculating the distance a car travels, the speed of an express train, and the time it takes for a snail to move a certain distance. Additionally, it includes more challenging problems like calculating the speed of a snake's attack and the time it would take for a rocket to travel from Earth to the Moon.

Mindmap
Keywords
💡Xcelerate Maths
Xcelerate Maths appears to be the name of the educational program or series from which the lesson is derived. It suggests a focus on mathematics education, aiming to accelerate or enhance the learning process. In the context of the video, it sets the stage for the mathematical concepts to be discussed, specifically the rules of speed, distance, and time.
💡Speed
Speed is a measure of how fast an object is moving, defined as the distance traveled per unit of time. It is a fundamental concept in physics and is crucial in understanding motion. In the video, speed is one of the three core components used in the DST (Distance, Speed, Time) triangle, and it is used to calculate both distance and time given the other two variables.
💡Distance
Distance refers to the total length of the path traveled by an object, independent of its direction (as opposed to displacement, which considers direction). In the context of the video, distance is a key element in the mathematical relationships being explored, used to determine both speed and time when the other variable is known.
💡Time
Time is the measure of the duration of events or the intervals between them. In the mathematical context of the video, time is one of the variables in the speed, distance, and time relationships, used to calculate speed or distance when the other quantities are known.
💡DST Triangle
The DST Triangle is a mnemonic device used in the video to remember the relationships between Distance (D), Speed (S), and Time (T). It is a tool for organizing the three rules in a way that is easy to recall and apply. The triangle helps to visualize the order and relationship of the variables, aiding in the understanding and application of the mathematical rules.
💡Rules of Speed, Distance, and Time
The rules of Speed, Distance, and Time are fundamental mathematical relationships that describe the dynamics of motion. These rules are used to calculate one of the three variables (speed, distance, or time) when the other two are known. They are essential in solving problems related to motion and are the core content of the video lesson.
💡Real-life Applications
Real-life applications refer to the practical use of mathematical concepts in everyday situations. In the video, the rules of speed, distance, and time are applied to various scenarios, such as car travel, train speeds, and the movement of a snail, to demonstrate their relevance and utility in understanding and solving real-world problems.
💡Challenge Question
A challenge question is a problem or question posed to test the understanding and application of a concept or set of concepts. In the video, challenge questions are used to engage the viewer and assess their grasp of the speed, distance, and time rules. These questions often involve more complex scenarios or require a deeper understanding of the mathematical relationships.
💡Rocket Travel
Rocket travel refers to the movement of a rocket, typically for space exploration or other interplanetary purposes. In the video, the concept is used to illustrate the application of the speed, distance, and time rules on a large scale, specifically in calculating the duration of a journey from Earth to the Moon.
💡Mnemonic Device
A mnemonic device is a technique or tool that aids in memory retention and recall. In the video, the DST Triangle serves as a mnemonic device to help remember the relationships between distance, speed, and time, facilitating the learning and application of the mathematical rules.
💡Unit Conversion
Unit conversion is the process of changing a physical quantity from one unit to another. It is an essential skill in many areas of science and mathematics, including the calculations of speed, distance, and time. In the video, unit conversion is necessary when expressing the duration of the rocket's journey from seconds to minutes and hours.
Highlights

Introduction to Xcelerate Maths and the topic of speed, distance, and time rules.

The use of a DST triangle to remember the three rules in alphabetical order.

Finding the distance rule by multiplying speed by time.

Using the triangle to derive the speed rule by dividing distance by time.

Determining the time rule by dividing distance by speed.

A practical example of calculating the distance a car travels.

Calculating the speed of an express train given its distance and time.

An example of finding the time it takes for a snail to move a certain distance.

A challenge question about calculating a snake's speed during an attack.

Another challenge involving calculating the time for a rocket to travel from Earth to the Moon.

The method of converting seconds to minutes and hours for the rocket's journey.

The final answer of 15.25 hours for the rocket's travel time.

The call to action for viewers to like and subscribe.

The lesson's focus on applying mathematical rules to real-life situations.

The importance of memorization techniques in learning mathematical concepts.

The practical applications of speed, distance, and time calculations in various scenarios.

The use of relatable examples to illustrate mathematical concepts, such as the car and snail examples.

The inclusion of challenge questions to engage and test the audience's understanding.

Transcripts

Browse More Related Video

Speed Distance Time Grade 8

Speed, Distance and Time

Speed, Distance, Time - Corbettmaths

Speed, distance and time

Maths Bitesize - The DST Triangle

Velocity - speed, distance and time - math lesson

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsEducationDST TriangleSpeed CalculationDistance LearningTime ManagementReal-Life MathTutorialLearning HackPhysics