Maths Bitesize - The DST Triangle
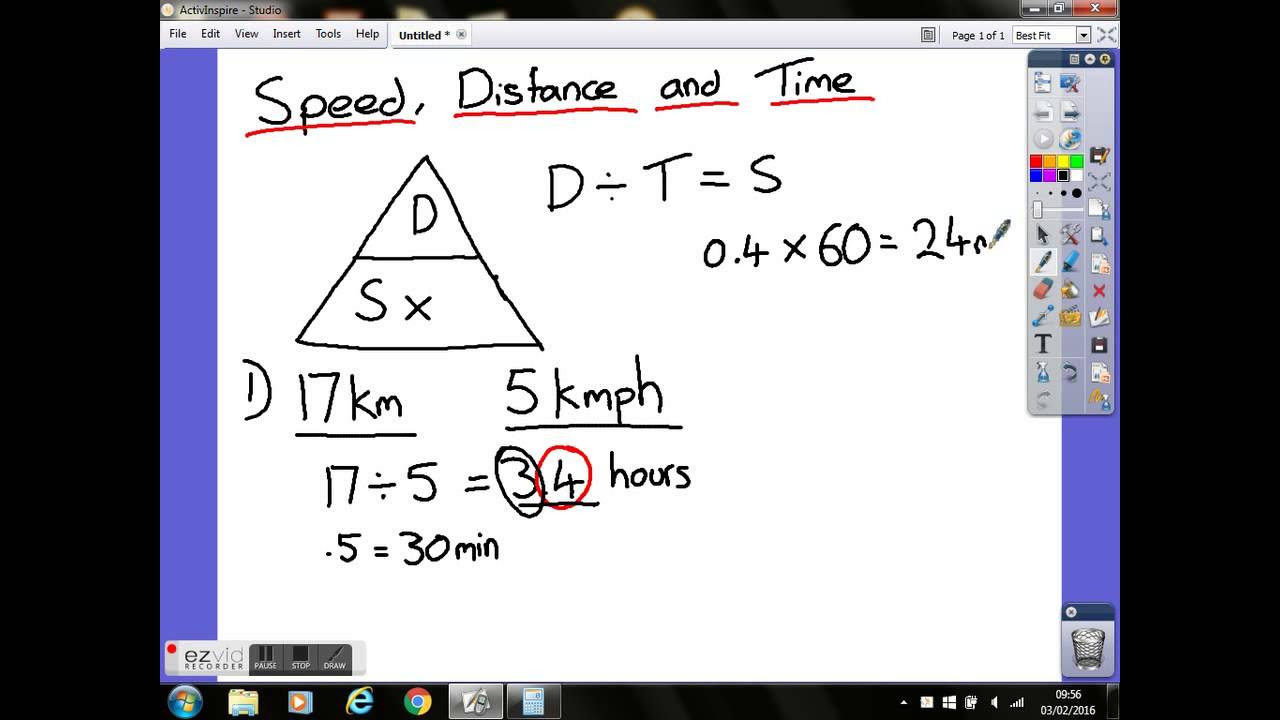
TLDRThe video script introduces the DST triangle, a mnemonic tool to help remember the relationships between distance, speed, and time. The letters D, S, and T are arranged alphabetically and separated by lines. To find a formula, one covers the letter representing the unknown variable. For instance, to find speed (S), cover S to reveal distance divided by time. The script demonstrates how to use the triangle with three examples: calculating the speed of a car that travels 5 miles in 6 minutes, finding the distance an airplane travels at 400 mph for 3.5 hours, and determining the time it takes to cycle 84 km at a speed of 24 km/h. The examples show conversions between units and the application of the DST triangle to solve practical problems, encouraging viewers to practice using the triangle for similar questions.
Takeaways
- 📐 The DST triangle is a mnemonic tool used to remember the relationships between distance (D), speed (S), and time (T).
- 🔍 The letters in the DST triangle are arranged in alphabetical order: D, S, T.
- 🤔 To find a formula, cover the letter representing the unknown variable you want to solve for.
- ⏱️ To calculate speed, divide distance by time (D/T).
- 🚗 To calculate distance, multiply speed by time (S*T).
- ⏳ To calculate time, divide distance by speed (D/S).
- 🔢 For the car example, to find speed in miles per hour (MPH), convert minutes to hours and then divide the distance by the time.
- ✈️ For the airplane example, to find distance traveled, multiply the speed by the time.
- 🚴 For the cycling example, to find the time taken, divide the distance by the speed.
- 📝 It's important to convert units (like minutes to hours) before performing calculations to maintain accuracy.
- 📈 The DST triangle helps in visualizing the mathematical relationship between the three variables and aids in solving related problems.
- 📚 Practicing with the DST triangle can enhance problem-solving skills for distance, speed, and time questions.
Q & A
What is the purpose of the DST triangle?
-The purpose of the DST triangle is to help remember the formulas for speed, distance, and time by arranging the letters D, S, and T in alphabetical order and using them to find the required formula by covering the letter that is not needed.
How do you lay out the letters in the DST triangle?
-The letters are arranged in alphabetical order: D, S, T, and then dividing lines are added between them to help remember the formulas.
If you need to find the speed of an object, how should you use the DST triangle?
-To find the speed, cover up the letter 'S' on the DST triangle, which shows that distance is divided by time.
What is the formula for speed when using the DST triangle?
-The formula for speed is distance divided by time, represented as Speed = Distance / Time.
How do you find the distance an object has traveled using the DST triangle?
-To find the distance, cover up the letter 'D', which leaves you with speed multiplied by time, represented as Distance = Speed * Time.
What is the formula for time when using the DST triangle?
-The formula for time is distance divided by speed, represented as Time = Distance / Speed.
If a car takes 6 minutes to travel 5 miles, how do you calculate its speed in miles per hour?
-First, convert 6 minutes to hours by dividing by 60. Then, divide the distance (5 miles) by the time in hours to find the speed in miles per hour.
An airplane flew at 400 mph for 3 and 1/2 hours. How far did it travel?
-Multiply the speed (400 mph) by the time (3.5 hours) to find the distance traveled, which is 1,400 miles.
Brian is planning to cycle 84 km to a hotel at a constant speed of 24 km/h. How long will it take him to get there?
-Divide the distance (84 km) by the speed (24 km/h) to find the time it will take, which is 3 and 1/2 hours.
How do you convert minutes to hours?
-To convert minutes to hours, divide the number of minutes by 60.
What is the significance of the dividing lines in the DST triangle?
-The dividing lines in the DST triangle help to visually separate the letters and make it easier to cover up one letter to find the formula for the remaining two variables.
How can the DST triangle be used to practice and reinforce the understanding of speed, distance, and time relationships?
-By using the DST triangle to cover up one variable and solving for the other two in various scenarios, it helps to practice and reinforce the understanding of how speed, distance, and time are interrelated in different problems.
Outlines
📐 Understanding the DST Triangle for Speed, Distance, and Time
The paragraph introduces the DST triangle as a mnemonic device to remember the relationships between speed, distance, and time. It explains that the letters D, S, and T are arranged alphabetically and separated by dividing lines. To find the formula for a specific variable, one simply covers up the letter representing the variable they do not need. For example, to find speed, one covers up 'S', leaving 'D' and 'T', indicating that distance divided by time gives speed. The paragraph also provides examples of how to use the triangle to solve for speed, distance, and time using real-world scenarios.
Mindmap
Keywords
💡DST Triangle
💡Speed
💡Distance
💡Time
💡Formula
💡Alphabetical Order
💡Covering Up
💡Conversion
💡MPH (Miles Per Hour)
💡Multiplication
💡Division
💡Constant Speed
Highlights
The DST triangle is a mnemonic tool used to remember the relationships between distance, speed, and time.
The letters in the DST triangle are arranged in alphabetical order: D for distance, S for speed, and T for time.
To find a formula, cover the letter representing the variable you need to calculate.
For calculating speed, cover the S in the triangle to reveal the formula: distance divided by time.
To find the distance an object has traveled, cover the D to show speed multiplied by time.
For determining the time an object has traveled, cover the T to find the formula: distance divided by speed.
An example problem involves a car traveling 5 miles in 6 minutes, with the solution being 50 mph after converting minutes to hours.
Another example calculates the distance an airplane traveled, flying at 400 mph for 3.5 hours, resulting in 1,400 miles.
The final example involves Brian cycling 84 km to a hotel at a constant speed of 24 km/h, with the time taken calculated as 3.5 hours.
The DST triangle is a practical tool for solving problems involving speed, distance, and time.
The triangle helps to organize and simplify the process of finding formulas for speed, distance, and time calculations.
Speed is calculated by dividing the distance by the time taken.
Distance is found by multiplying the speed by the time taken.
Time is determined by dividing the distance by the speed.
Unit conversion is necessary when performing calculations, such as converting minutes to hours.
The DST triangle can be applied to various real-world scenarios, such as calculating speeds of vehicles or travel times.
The method is straightforward and can be easily understood and applied by learners.
Practicing with the DST triangle helps solidify the understanding of the relationship between distance, speed, and time.
The transcript provides a step-by-step guide on how to use the DST triangle for different types of problems.
The DST triangle is a versatile tool that can be used to solve a variety of problems related to motion and travel.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: