Speed, distance and time
TLDRThis tutorial focuses on the concepts of speed, distance, and time, which are occasionally encountered in functional skills tests. It offers a straightforward method to solve problems involving these three variables using a speed-distance-time triangle. The triangle helps to identify the correct calculation needed based on which variable is being sought. For instance, to find speed, one would use the formula distance divided by time equals speed. The video provides a step-by-step approach to solving example problems, such as calculating time given distance and speed, and distance given speed and time. It also explains how to convert decimal hours into minutes for time calculations. The key takeaway is that by using the triangle and understanding the relationships between speed, distance, and time, one can easily solve complex problems related to these concepts.
Takeaways
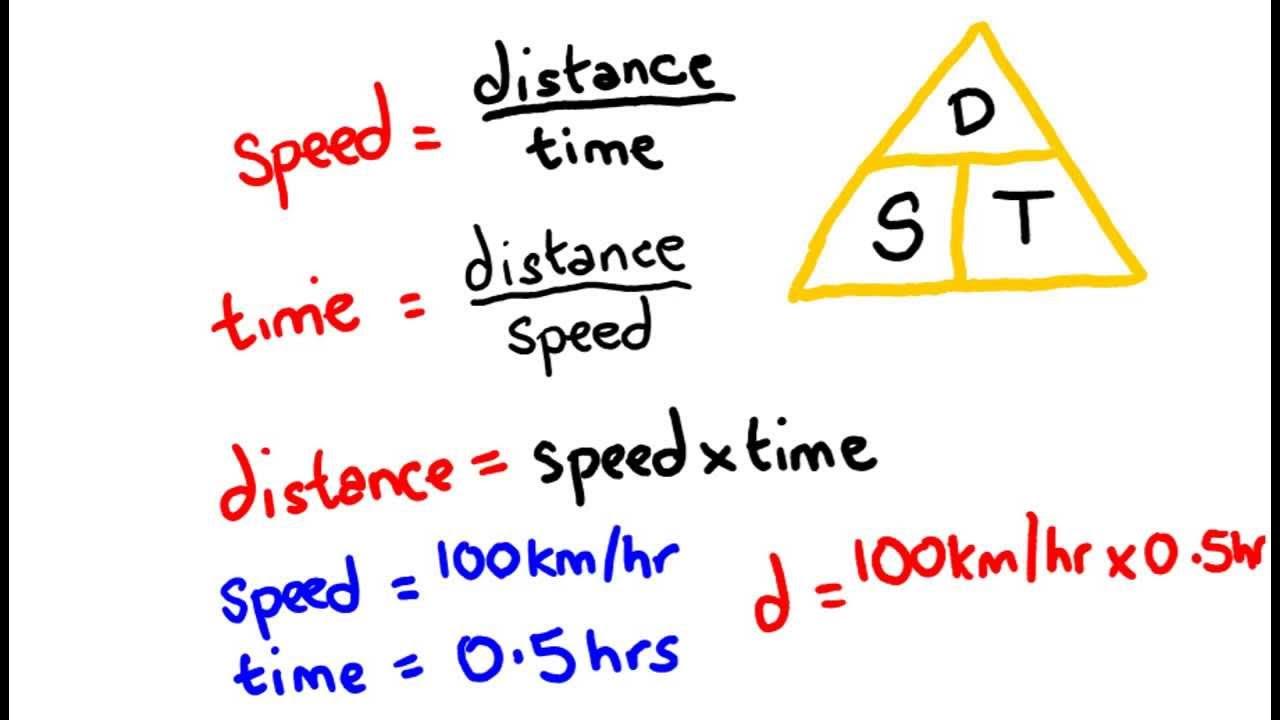
- 📐 **Speed, Distance, and Time Triangle**: Understanding the relationship between speed, distance, and time can be simplified using a triangle model where distance is at the top and speed and time are at the sides, with multiplication between them.
- 🚗 **Calculating Speed**: To find speed, divide the distance by the time. This is the formula: Speed = Distance / Time.
- ⏱️ **Calculating Time**: To find time, divide the distance by the speed. This is the formula: Time = Distance / Speed.
- 📏 **Calculating Distance**: To find distance, multiply speed by time. This is the formula: Distance = Speed * Time.
- 🔢 **Using a Calculator**: For functional skills tests, you are usually allowed to use a calculator to solve these problems, simplifying the process.
- 🕒 **Understanding Time**: Decimal hours can be converted to minutes by multiplying the decimal by 60 (e.g., 0.4 hours is 0.4 * 60 = 24 minutes).
- 📚 **Practice Makes Perfect**: The more you practice with speed, distance, and time problems, the easier it becomes to solve them quickly and accurately.
- 🧮 **Breaking Down the Problem**: When faced with a problem, identify which of the three variables (speed, distance, time) you are looking for and eliminate it from the triangle to determine the calculation needed.
- 🚴 **Example Problem Solving**: The tutorial provides examples of calculating time given distance and speed, and distance given speed and time, demonstrating the application of the formulas.
- ⏰ **Time Conversion Clarification**: It's clarified that 0.4 hours is not 40 minutes but rather 24 minutes, emphasizing the importance of understanding decimal hour conversion.
- 📈 **Building Confidence**: By repeatedly working through example questions, one can build confidence in handling speed, distance, and time problems.
- 🔁 **Repeating the Process**: The process of solving these types of problems is consistent, making it easier to tackle more complex questions once the basic method is mastered.
Q & A
What are the three key components in the context of speed, distance, and time calculations?
-The three key components are speed, distance, and time. They are interconnected and can be used to calculate one another given the other two.
What is the formula to calculate speed when distance and time are known?
-The formula to calculate speed is distance divided by time, represented as Speed = Distance / Time.
How can you determine the time taken when you know the distance and speed?
-You can determine the time taken by dividing the distance by the speed, which is Time = Distance / Speed.
What is the relationship between hours and minutes in the context of the script?
-0.5 of an hour is equal to 30 minutes. To convert a decimal hour to minutes, you multiply the decimal by 60.
How do you interpret 3.4 hours in terms of hours and minutes?
-3.4 hours means 3 hours and 24 minutes. The whole number represents the hours, and the decimal (when multiplied by 60) represents the minutes.
What is the purpose of the speed, distance, and time triangle mentioned in the script?
-The triangle is a visual tool to help remember the relationships between speed, distance, and time, and to determine which calculation to perform based on the variables you are trying to solve for.
What is the formula to calculate distance when speed and time are known?
-The formula to calculate distance is speed multiplied by time, represented as Distance = Speed * Time.
How much distance was covered in the example where the speed was 42 miles per hour and the time was 6 hours?
-The distance covered was 252 miles, calculated by multiplying the speed (42 miles per hour) by the time (6 hours).
Why is it important to practice calculations involving speed, distance, and time?
-Practice is important because it helps to build familiarity with the calculations, making it easier to solve more complex problems involving these three variables.
What is the general approach to solving problems involving speed, distance, and time?
-The general approach is to identify which of the three variables (speed, distance, time) you are trying to find, then use the appropriate formula (either Speed = Distance / Time or Distance = Speed * Time) to calculate it.
In the context of functional skills tests, are calculators typically allowed for speed, distance, and time calculations?
-Yes, in functional skills tests, calculators are typically allowed to assist with these calculations.
What is a common misconception about interpreting decimal hours in terms of minutes?
-A common misconception is to interpret 0.4 hours as 40 minutes. The correct interpretation is that 0.4 hours is 24 minutes, as you multiply the decimal by 60 to get the minutes.
Outlines
📚 Understanding Speed, Distance, and Time
This paragraph introduces the concept of speed, distance, and time, which may not frequently appear in functional skills tests but can be challenging when encountered. It emphasizes the use of a speed-distance-time triangle for calculations. The triangle helps to determine the necessary calculations by covering the variable you're not looking for. An example problem is solved, where a person has run 17 km at a speed of 5 km/h to find the time taken, which is 3.4 hours. The explanation clarifies how to interpret decimal hours as minutes, with 0.4 hours being equivalent to 24 minutes. This provides a clear method for solving related problems.
🚗 Applying the Formula for Distance
The second paragraph focuses on applying the speed, distance, and time formula to find the distance covered. It discusses the importance of practice in getting accustomed to these types of problems. A new example is provided where a car travels at a speed of 42 miles per hour for 6 hours. Using the triangle method, the calculation involves multiplying speed by time to find the distance, which in this case is 252 miles. The paragraph concludes by reiterating the simplicity of the process once the correct calculation is identified and emphasizes the ease of solving such problems with practice.
Mindmap
Keywords
💡Speed
💡Distance
💡Time
💡Functional Skills
💡Calculation
💡Triangle
💡Map Reading
💡Practice
💡Conversion
💡Decimals
💡Miles per Hour (mph)
Highlights
Speed, distance, and time are important concepts that can come up in functional skills tests.
People often panic when they see speed, distance, and time problems, but there are tips to make it easier.
The speed, distance, and time triangle is a useful tool to help with these calculations.
The triangle shows that distance divided by time equals speed.
To solve a problem, cover up or remove the variable you are trying to find.
The first example is calculating time given distance and speed.
In the first example, the distance is 17 km and the speed is 5 km/h.
Dividing the distance by the speed gives the time, which is 3.4 hours in the first example.
0.4 hours is equivalent to 24 minutes, not 40 minutes.
The trick is to take the decimal part and multiply by 60 to convert to minutes.
In the first example, the total time is 3 hours and 24 minutes.
Practice is key to getting comfortable with these types of problems.
The second example is calculating distance given speed and time.
In the second example, the speed is 42 miles per hour and the time is 6 hours.
Multiplying the speed by the time gives the distance, which is 252 miles in the second example.
The formula is speed multiplied by time equals distance.
Always remove the variable you are trying to find before doing the calculation.
This tutorial provides a simple method for solving speed, distance, and time problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: