Speed, Distance, Time - Corbettmaths
TLDRThis video script provides a comprehensive overview of the relationship between speed, distance, and time. It explains that speed is the measure of how far an object travels in a given time frame, and it can be expressed in various units such as miles per hour (mph), kilometers per hour (km/h), or meters per second (m/s). The script outlines three key formulas: speed equals distance divided by time (S = D/T), distance equals speed times time (D = S*T), and time equals distance divided by speed (T = D/S). It also emphasizes the importance of converting time units to ensure consistency in calculations. The video includes several examples to illustrate how to calculate average speed, distance traveled, and duration of a journey using these formulas. It concludes with a reminder to be careful with time unit conversions when dealing with mixed units like hours and minutes.
Takeaways
- 📏 Speed is a measure of how far you travel in a certain amount of time, often expressed in units like miles per hour (mph) or kilometers per hour (km/h).
- 🔢 The formula for speed is Speed = Distance / Time, which can be rearranged to find distance or time given the other two variables.
- ⏱️ To convert minutes to hours, divide by 60, and to convert hours to minutes, multiply by 60.
- 🚗 For the car traveling at 30 mph, it will cover 30 miles in 1 hour, 60 miles in 2 hours, and so on, following the pattern of multiplying speed by time.
- 🏃 Speed can also be measured in meters per second (m/s), which might be used for sprinters or other short-duration activities.
- 🔄 The relationship between speed, distance, and time is fundamental for solving problems involving these variables.
- ✅ To find the average speed, use the formula Speed = Total Distance / Total Time, ensuring units match (e.g., miles per hour).
- 🕒 To find the distance traveled, use the formula Distance = Speed * Time, which helps in calculating how far an object has moved.
- 🕗 To find the time taken, use the formula Time = Distance / Speed, which is useful for determining the duration of a journey.
- 🛫 In problems involving mixed units of time (e.g., hours and minutes), convert all time measurements to a single unit (usually hours) before applying the formulas.
- 📐 When calculating time in hours and minutes, if you have a decimal hour, multiply it by 60 to find the equivalent number of minutes.
- 🧮 Practice converting between different units of speed (e.g., from km/h to m/s or mph to km/h) to apply the formulas accurately in various contexts.
Q & A
What is the speed of a car traveling at a speed limit of 30 miles per hour?
-The speed of the car is 30 miles per hour, which means it travels 30 miles in one hour.
How is speed defined in terms of distance and time?
-Speed is defined as the distance traveled divided by the time taken to travel that distance.
What are the different units used to measure speed?
-Speed can be measured in miles per hour (mph), kilometers per hour (km/h), or meters per second (m/s).
If a car travels 60 miles in two hours, what is its speed?
-The speed of the car is 30 miles per hour, calculated by dividing the distance (60 miles) by the time (2 hours).
How do you calculate the distance a vehicle travels if you know its speed and time?
-You calculate the distance by multiplying the speed by the time the vehicle travels.
If a train travels 175 miles at an average speed of 25 miles per hour, how long does the journey last?
-The journey lasts 7 hours, calculated by dividing the distance (175 miles) by the speed (25 mph).
How do you calculate the average speed of a bird that flies for six hours at an average speed of 40 kilometers per hour?
-The bird travels 240 kilometers, calculated by multiplying the speed (40 km/h) by the time (6 hours).
How do you calculate the average speed of a helicopter that flies 200 miles in 2 hours and 30 minutes?
-The average speed is 80 miles per hour, calculated by dividing the distance (200 miles) by the time in hours (2.5 hours).
If Roger drives for 2 hours and 15 minutes at an average speed of 30 miles per hour, how far does he travel?
-Roger travels 81 miles, calculated by multiplying the speed (30 mph) by the time in hours (2.25 hours).
How do you calculate the average speed of a car that travels 240 kilometers in 3 hours and 40 minutes?
-The average speed is 65.45 kilometers per hour, calculated by dividing the distance (240 km) by the time in hours (3.67 hours).
If a lorry travels 210 miles at an average speed of 50 miles per hour, how long does the journey last?
-The journey lasts 4 hours and 12 minutes, calculated by dividing the distance (210 miles) by the speed (50 mph) and converting the decimal part of the hours into minutes.
How do you convert minutes into hours for calculations involving speed, distance, and time?
-You convert minutes into hours by dividing the number of minutes by 60. For example, 30 minutes is 0.5 hours, and 15 minutes is 0.25 hours.
Outlines
🚗 Understanding Speed, Distance, and Time
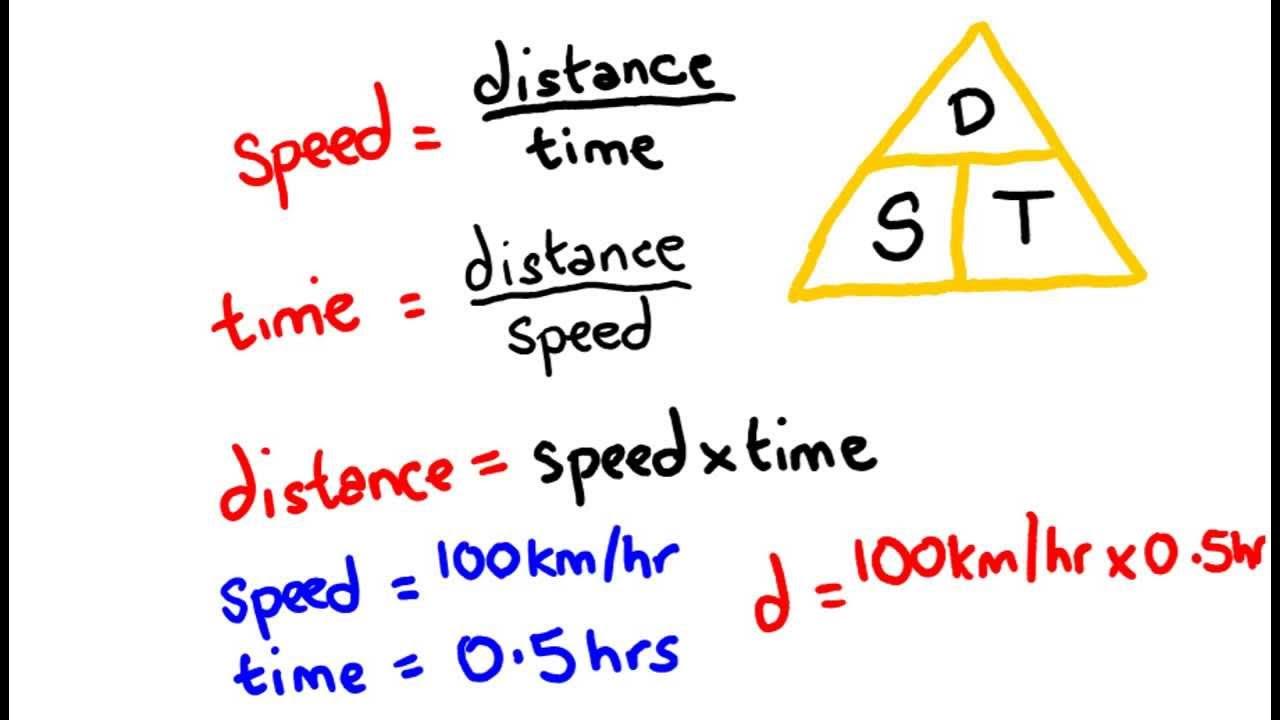
This paragraph introduces the fundamental concepts of speed, distance, and time. It explains that speed is the measure of distance traveled over time, and provides examples using miles per hour (mph), kilometers per hour (km/h), and meters per second (m/s). The relationship between speed, distance, and time is established through the formulas: Speed = Distance / Time, Distance = Speed * Time, and Time = Distance / Speed. The paragraph also demonstrates how to apply these formulas to solve problems involving constant speeds over varying durations.
📐 Applying Formulas to Calculate Speed and Distance
This section delves into applying the speed, distance, and time formulas to solve various problems. It covers how to calculate the average speed of a car traveling a certain distance in a given time, how to determine the distance covered by multiplying speed by time, and how to find the time taken by dividing distance by speed. The paragraph also addresses the conversion of time units from hours and minutes to a single unit (hours) for consistency in calculations. Examples include calculating the speed of a helicopter, the distance a bird flies, and the time taken for a train journey.
🕒 Converting Time Units and Calculating Journey Duration
The final paragraph focuses on the importance of converting time units to ensure accurate calculations. It demonstrates how to convert minutes into hours or fractions of an hour for use in speed, distance, and time calculations. The paragraph provides examples of calculating the average speed of a car and a lorry, and determining the duration of a journey in hours and minutes. It emphasizes the need to convert decimal hours into minutes by multiplying by 60, and concludes with a recap of the key relationships between speed, distance, and time.
Mindmap
Keywords
💡Speed
💡Distance
💡Time
💡Miles per hour (mph)
💡Kilometers per hour (km/h)
💡Meters per second (m/s)
💡Average Speed
💡Formulas
💡Exam Questions
💡Unit Conversion
💡Decimal Hours
Highlights
Speed is a measurement of how far you travel in a certain amount of time.
The formula for speed is speed equals distance divided by time (S = D/T).
The formula for distance is distance equals speed times time (D = S*T).
The formula for time is time equals distance divided by speed (T = D/S).
Different units of speed include miles per hour (mph), kilometers per hour (km/h), and meters per second (m/s).
To find the speed, divide the distance traveled by the time taken.
To find the distance, multiply the speed by the time traveled.
To find the time taken, divide the distance by the speed.
When calculating speed, ensure that the time unit matches the desired speed unit.
For exam questions, it's crucial to understand and apply the relationship between speed, distance, and time.
When time is given in hours and minutes, convert it to hours for calculations.
30 minutes is equal to 0.5 hours, and 15 minutes is 0.25 hours.
To convert decimal hours to minutes, multiply by 60.
When calculating average speed, include the units in the answer.
For complex time conversions, use fractions to simplify before converting to decimal form.
Always verify the calculated speed by checking if the distance can be obtained by multiplying the speed by the time.
When the time includes minutes, it's important to convert it to a decimal fraction of an hour for the calculation.
To calculate the duration of a journey in hours and minutes, use the decimal part of the hours to find the minutes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: