Speed, Distance and Time
TLDRThis informative video delves into the fundamental concepts of speed, distance, and time, illustrating how they interrelate in various contexts. The presenter explains that speed is the measure of distance traveled over time, using miles per hour (mph) as a common unit of measurement. The video outlines three key formulas: speed equals distance divided by time (s = d/t), distance equals speed times time (d = s*t), and time equals distance divided by speed (t = d/s). These relationships are further simplified using a mnemonic triangle for easy recall. The script progresses through several practical examples, including calculating the average speed of a car, a runner's pace in meters per second, and the duration of a train or helicopter journey. It emphasizes the importance of unit consistency and converting time measurements when necessary, such as from minutes to hours. The video concludes with a reminder to be cautious with mixed time units and to apply the correct conversion to ensure accurate results, providing a comprehensive understanding of the speed, distance, and time relationship.
Takeaways
- 📏 Speed is a measure of how far an object travels in a certain amount of time, often expressed in miles per hour (mph), kilometers per hour (km/h), or meters per second (m/s).
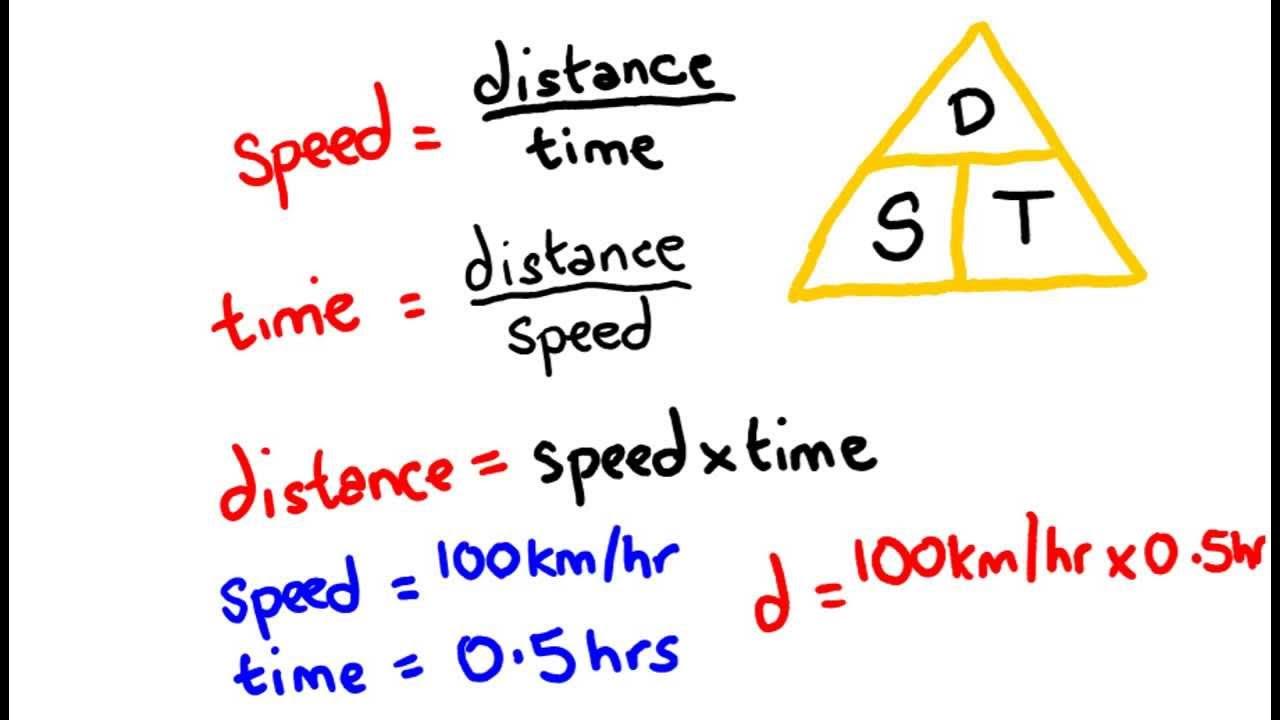
- ⏱️ The three fundamental relationships between speed (S), distance (D), and time (T) are: Speed = Distance / Time, Distance = Speed * Time, and Time = Distance / Speed.
- 🔢 To calculate the average speed of a vehicle, divide the total distance traveled by the total time taken, including ensuring units are consistent (e.g., mph, km/h).
- 🚗 For finding the distance covered, multiply the speed by the time traveled, which will give you the distance in the same units as the speed.
- ⏳ To determine the time taken for a journey, divide the total distance by the speed, converting the result to the desired time units.
- 🚀 Understanding the conversion between different units of time is crucial, such as knowing that 30 minutes is 0.5 hours and 15 minutes is 0.25 hours.
- 📐 Utilize the speed-distance-time triangle to remember the relationships and solve for the unknown variable by covering the variable you're solving for.
- 🧮 When dealing with a mix of hours and minutes, convert the entire time period into hours or minutes based on the required speed unit for accurate calculations.
- 🔄 Always check your calculations by substituting the calculated values back into the formula to ensure the original distance or time is obtained.
- 📝 When expressing the duration of a journey in hours and minutes, convert the decimal part of the hour into minutes by multiplying by 60.
- 🛣️ In exam questions, it's essential to pay attention to the units given and required, and to convert units as necessary to match the formula being used.
- 📈 Practice solving problems with different units and time frames to become proficient in applying the speed, distance, and time relationships in various contexts.
Q & A
What is the basic concept of speed?
-Speed is a measurement of how far you travel in a certain amount of time. It is commonly expressed in units such as miles per hour (mph) or kilometers per hour (km/h).
If a car travels at 30 miles per hour, how many miles will it cover in 4 hours?
-At 30 miles per hour, a car will cover 120 miles in 4 hours (30 miles/hour * 4 hours).
What are the three fundamental formulas relating speed, distance, and time?
-The three fundamental formulas are: Speed (S) = Distance (D) / Time (T), Distance (D) = Speed (S) * Time (T), and Time (T) = Distance (D) / Speed (S).
How can you remember the relationship between speed, distance, and time?
-You can use a triangle where you cover up the variable you are looking for, leaving you with the formula involving the remaining two variables.
If a car travels 180 miles in 4 hours, what is its average speed in miles per hour?
-The average speed is 45 miles per hour (180 miles / 4 hours).
How can you calculate the average speed of a runner who runs 400 meters in 50 seconds?
-The average speed is 8 meters per second (400 meters / 50 seconds).
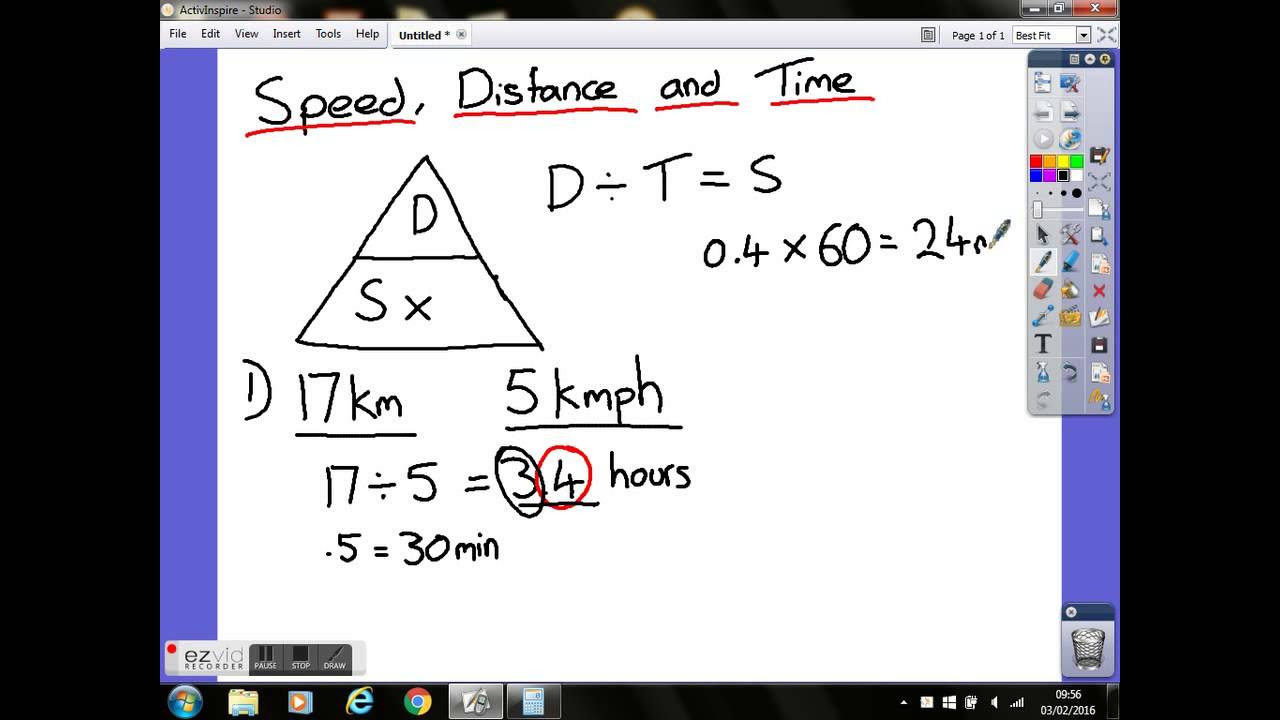
How long does a train journey last if it travels 175 miles at an average speed of 25 miles per hour?
-The journey lasts 7 hours (175 miles / 25 miles per hour).
If a bird flies for 6 hours at an average speed of 40 kilometers per hour, how far does it travel?
-The bird travels 240 kilometers (40 kilometers per hour * 6 hours).
How do you calculate the average speed of a helicopter that flies 200 miles in 2 hours and 30 minutes?
-First, convert the time to hours (2 hours and 30 minutes is 2.5 hours), then calculate the speed as 80 miles per hour (200 miles / 2.5 hours).
How far does Roger drive if he travels for 2 hours and 15 minutes at an average speed of 30 miles per hour?
-Roger drives 81 miles (30 miles per hour * 2.25 hours).
What is the average speed of a car that travels 240 kilometers in 3 hours and 40 minutes?
-The average speed is 65.45 kilometers per hour (240 kilometers / 3.67 hours).
How long does a journey last if a lorry travels 210 miles at an average speed of 50 miles per hour?
-The journey lasts 4 hours and 12 minutes (210 miles / 50 miles per hour = 4.2 hours, and 0.2 hours * 60 minutes = 12 minutes).
Outlines
🚗 Understanding Speed, Distance, and Time
This paragraph introduces the concepts of speed, distance, and time, focusing on how they are interrelated. It explains that speed is the measure of distance traveled over time and provides examples using miles per hour (mph), kilometers per hour (km/h), and meters per second (m/s). The paragraph also presents the fundamental formulas: speed equals distance divided by time, distance equals speed times time, and time equals distance divided by speed. These relationships are further illustrated with the help of a triangle mnemonic for easy recall.
🏃 Applying Formulas to Practical Problems
This section delves into applying the speed, distance, and time formulas to solve various problems. It covers how to calculate the average speed of a car that travels a certain distance in a given time, such as 180 miles in 4 hours, resulting in a speed of 45 mph. The paragraph also demonstrates how to calculate the average speed in different units, like meters per second for a runner, and how to determine the duration of a journey, such as a train traveling 175 miles at 25 mph, lasting 7 hours.
🚁 Calculating Speed with Mixed Time Units
This paragraph addresses the challenge of calculating speed when the time unit is mixed, such as hours and minutes. It explains the process of converting minutes into hours or fractions/decimals of an hour to maintain consistency in units. Examples include calculating the average speed of a helicopter that flies 200 miles in 2 hours and 30 minutes, resulting in an average speed of 80 mph, and a car that travels 240 kilometers in 3 hours and 40 minutes, with an average speed of approximately 65.45 km/h.
🚛 Converting Decimal Hours to Minutes
The final paragraph discusses how to handle calculations when the time unit is in decimal hours, such as a lorry traveling 210 miles at an average speed of 50 mph, which lasts for 4.2 hours. It shows how to convert the decimal part of the hour into minutes by multiplying by 60, resulting in a journey duration of 4 hours and 12 minutes. The paragraph emphasizes the importance of converting time units to ensure accurate calculations and understanding of speed, distance, and time relationships.
Mindmap
Keywords
💡Speed
💡Distance
💡Time
💡Miles per hour (mph)
💡Kilometers per hour (km/h)
💡Meters per second (m/s)
💡Average Speed
💡Formula
💡Conversion of Time
💡Units
💡Exam Questions
Highlights
Speed is a measurement of how far you travel in a certain amount of time.
Speed can be expressed in various units like miles per hour (mph), kilometers per hour (km/h), or meters per second (m/s).
The relationship between speed, distance, and time can be represented by the formula: speed = distance/time.
Distance traveled can be calculated by multiplying speed by time: distance = speed × time.
To find the time taken, divide the distance by the speed: time = distance/speed.
A mnemonic for remembering the relationship between speed, distance, and time is to cover up the variable you're solving for, leaving you with the formula to use.
When dealing with different units of time, such as hours and minutes, it's important to convert them to a single unit, usually hours.
For example, 30 minutes is equal to 0.5 hours, and 15 minutes is 0.25 hours.
To calculate the average speed of a car that traveled 180 miles in 4 hours, use the formula speed = distance/time, resulting in 45 mph.
Kevin's average speed running 400 meters in 50 seconds is 8 meters per second (m/s).
A train traveling 175 miles at 25 mph lasts for 7 hours, calculated by time = distance/speed.
A bird flying for 6 hours at an average speed of 40 km/h travels 240 kilometers.
A helicopter flying 200 miles in 2 hours and 30 minutes has an average speed of 80 mph.
Roger drives for 2 hours and 15 minutes at 30 mph, covering a distance of 81 miles.
A car traveling 240 kilometers in 3 hours and 40 minutes has an average speed of approximately 65.45 km/h.
A lorry traveling 210 miles at 50 mph lasts for 4 hours and 12 minutes when converted from decimal hours to hours and minutes.
Always be careful to convert mixed time units into the unit required by the speed, distance, and time formula being used.
Understanding and applying the relationships between speed, distance, and time is crucial for solving various problems in physics and everyday scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: