Speed Distance Time Grade 8

Kevinmathscience
29 Jan 202413:07
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is an educational lesson focused on the concepts of speed, distance, and time, and their interrelations. The instructor introduces a mnemonic device—a triangle—to help students remember the formulas for calculating each variable. The triangle has 'D' for distance at the top, and 'S' for speed and 'T' for time at the bottom. The formulas are as follows: Speed (S) equals Distance (D) divided by Time (T), Time (T) equals Distance (D) divided by Speed (S), and Distance (D) equals Speed (S) multiplied by Time (T). The lesson continues with several practice problems, applying these formulas to find speed, time, and distance in different scenarios. The instructor emphasizes the importance of using consistent units for calculations and provides real-world context, such as looking at a car's dashboard for speed measurements. The lesson concludes with a problem involving a car driving at a constant speed and calculating the time it would take to cover a certain distance, reinforcing the application of the learned formulas.

Takeaways
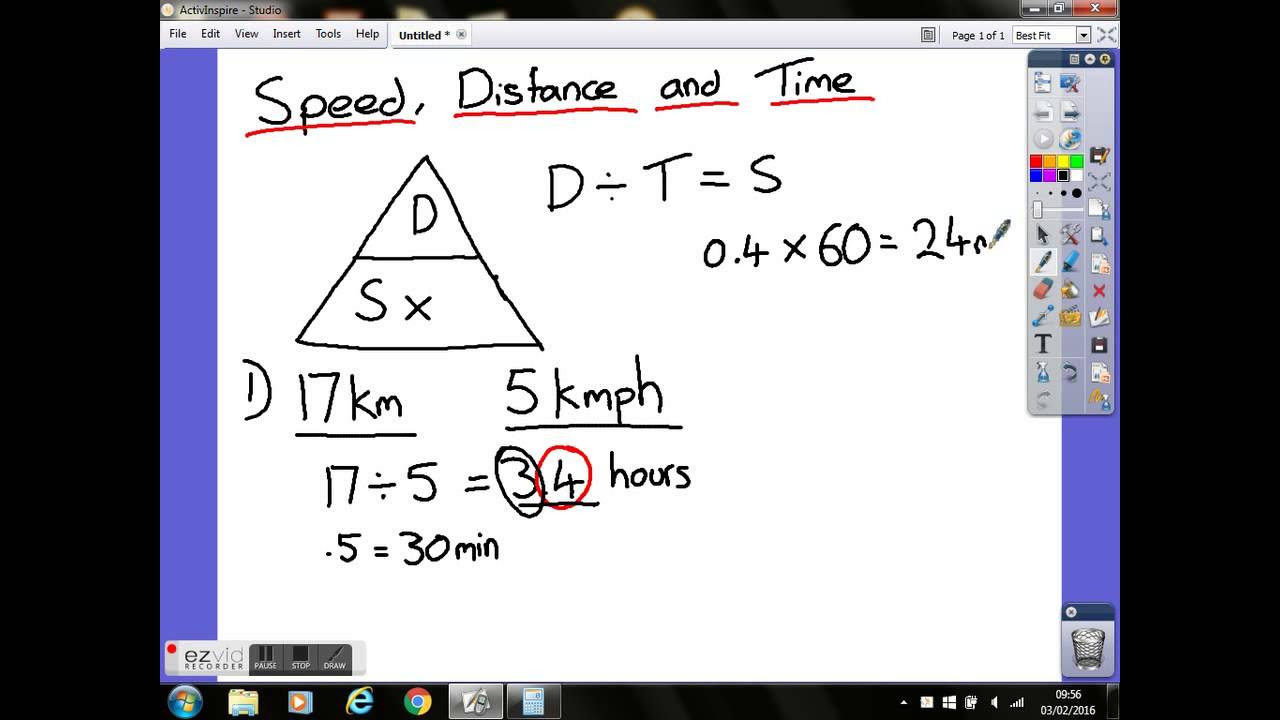
  • 📐 **Understanding the Triangle**: The lesson introduces a triangle model to help remember the relationship between distance (D), speed (S), and time (T), with distance at the top and speed and time at the bottom.
  • ⚖️ **Speed Formula**: Speed is calculated as distance divided by time (S = D/T), which is a fundamental concept for solving problems involving motion.
  • ⏱️ **Time Formula**: To find the time taken, use the formula time equals distance divided by speed (T = D/S).
  • 📏 **Distance Formula**: Distance is found by multiplying speed by time (D = S*T), which is useful when you know how fast something is moving and for how long.
  • 🚗 **Units of Speed**: Speed is measured in kilometers per hour (km/h), which is a standard unit to express how fast something is moving.
  • 🔢 **Practical Example**: The script provides an example of calculating the speed of a car that drives 100 km in 2 hours, resulting in a speed of 50 km/h.
  • 🗺️ **Time to Destination**: It explains how to calculate the time required to travel a certain distance at a given speed, using the formula T = D/S.
  • 🚘 **Distance Calculation**: The lesson shows how to find the distance covered when given speed and time, using the formula D = S*T.
  • 🏎️ **Consistent Speed Assumption**: In problems where multiple parts are involved, it's often assumed that the speed remains constant unless stated otherwise.
  • ⏳ **Time Conversion**: When calculating speed, it's important to ensure that the units of time are consistent with the units of distance.
  • 📉 **Speed Comparison**: The script illustrates how to compare speeds by calculating them and then determining which is faster.
  • 🔄 **Maintaining Speed**: In the context of the problems, it's assumed that unless specified, the speed of a vehicle does not change throughout the journey.
Q & A

  • What is the basic concept of the triangle used to remember the formulas for speed, distance, and time?

    -The triangle has distance (D) at the top and speed (S) and time (T) at the bottom. It helps to remember the relationships between these three variables: Speed is distance divided by time (S = D/T), time is distance divided by speed (T = D/S), and distance is speed multiplied by time (D = S*T).

  • How is speed typically measured in a vehicle?

    -Speed is typically measured in kilometers per hour (km/h) on a vehicle's dashboard.

  • If a car drives 100 km in 2 hours, what is the speed of the car?

    -The speed of the car is 50 km/h, calculated by dividing the distance (100 km) by the time (2 hours).

  • What is the formula to calculate the time taken to travel a certain distance at a given speed?

    -The formula to calculate time (T) is T = D/S, where D is the distance and S is the speed.

  • How long will it take to drive from Durban to Cape Town if the distance is 1650 kilometers and the speed is 120 kilometers per hour?

    -It will take 13.75 hours to drive from Durban to Cape Town at a speed of 120 km/h.

  • If a car is driving at 60 km/h for 4.5 hours, what distance does it cover?

    -The car will cover a distance of 270 km, calculated by multiplying the speed (60 km/h) by the time (4.5 hours).

  • What is the speed of a vehicle driving 250 km in 4 hours?

    -The speed of the vehicle is 62.5 km/h, calculated by dividing the distance (250 km) by the time (4 hours).

  • If a car drives 350 km in 6 hours, what is the average speed of the car?

    -The average speed of the car is 58.33 km/h, calculated by dividing the distance (350 km) by the time (6 hours).

  • What is the key assumption made when calculating the distance for the next part of a journey, given a constant speed?

    -The key assumption is that the speed of the car remains the same for the next part of the journey, without any acceleration or deceleration.

  • How long will it take for a car to drive 520 km at a constant speed of 50 km/h?

    -It will take 10.4 hours to drive 520 km at a constant speed of 50 km/h.

  • If Morgan drives 100 km in 80 minutes, what is the speed in kilometers per minute?

    -Morgan's speed is 1.25 km/min, calculated by dividing the distance (100 km) by the time (80 minutes).

  • How far will a car travel in 140 minutes at a speed of 1.25 km/min?

    -The car will travel 175 km in 140 minutes at a speed of 1.25 km/min, calculated by multiplying the speed (1.25 km/min) by the time (140 minutes).

Outlines
00:00
📚 Introduction to Rate, Speed, Distance, and Time

This paragraph introduces the concepts of rate, speed, distance, and time. The speaker explains the importance of understanding these concepts and how they relate to one another. The key formulas for calculating speed (distance divided by time), time (distance divided by speed), and distance (speed multiplied by time) are presented. A mnemonic device in the form of a triangle is suggested to help remember the relationship between these variables, with distance at the top and speed and time at the bottom. An example is given to demonstrate how to use the triangle to solve for speed when given distance and time.

05:04
🚗 Applying the Formulas to Real-World Scenarios

The speaker continues by applying the formulas to various scenarios involving vehicles and their speeds. Examples include calculating the speed of a car that drives 100 km in 2 hours, determining the time it would take to drive from Durban to Cape Town at a speed of 120 km/h, and finding the distance a car would travel at 60 km/h for a certain amount of time. The importance of including units when stating the answer is emphasized, specifically using kilometers per hour for speed. The paragraph also touches on the assumption that speed remains constant in these calculations unless otherwise stated.

10:04
🚦 Further Examples and Calculations with Different Units

The final paragraph provides additional examples to reinforce the understanding of the formulas. It includes calculating the speed of a person named Nandy driving 250 km in 4 hours and another person, Andrea, driving 350 km in 6 hours. The speaker also discusses calculating the time it would take for a person named Amy to drive a certain distance at a constant speed of 50 km/h. The importance of using consistent units for time and distance in calculations is highlighted, with an example of calculating distance when the speed is given in kilometers per minute and the time in minutes. The paragraph concludes with an example involving Morgan, assuming a constant speed and calculating the distance driven in a given amount of time.

Mindmap
Keywords
💡Rate
Rate, in the context of the video, refers to speed, which is a measure of how fast something is moving. It is a fundamental concept in physics and is directly related to the theme of the video, which is about understanding and calculating speed, distance, and time. For example, the script mentions 'we explained exactly how rate works,' indicating that rate is a key component in solving problems involving motion.
💡Speed
Speed is the distance an object travels per unit of time. It is a scalar quantity and is typically measured in kilometers per hour (km/h) or meters per second (m/s). In the video, speed is calculated using the formula speed = distance / time, which is central to solving the problems presented. For instance, the script states 'if you want to find speed it's over here now have a look you're going to say equals and then you see that the distance is at the top and then the time is over there so you're going to say distance divided by time.'
💡Distance
Distance is the scalar quantity that represents the total length of the path traveled by an object. It is a measure of how far an object has moved from a starting point. In the video, distance is one of the variables in the speed, distance, time relationship and is used to calculate speed and time. An example from the script is 'a car drives 100 km that's the distance,' which is used to find the speed of the car.
💡Time
Time is the measure in which events can be ordered from the past through the present into the future, and also the measure of durations of events and the intervals between them. In the context of the video, time is one of the key variables in motion problems, used alongside speed and distance to solve for unknowns. The script illustrates this with examples such as 'in 2 hours that's the time' when calculating the speed of a car that has traveled a certain distance.
💡Formulas
Formulas are mathematical statements that express a relationship between different quantities. In the video, formulas are used to relate speed, distance, and time to each other. The script emphasizes the importance of memorizing these formulas for solving problems, as indicated by 'I'm going to give you formulas for Speed, distance, time and then it will make it a lot easier.'
💡Triangle Diagram
The triangle diagram is a mnemonic device used in the video to help remember the relationships between speed, distance, and time. It places distance at the top, and speed and time at the bottom, to visually represent the formulas for calculating each variable. The script instructs viewers to 'draw a triangle for yourself' and use it to remember the formulas, which aids in solving the problems discussed.
💡Kilometer per Hour (km/h)
Kilometer per hour is a unit of speed in the metric system, expressing the distance an object can travel in one hour. It is used in the video to measure the speed of vehicles. For example, the script mentions 'speed is measured in kilometers per hour' when discussing the speed of a car driving 100 km in 2 hours, resulting in a speed of 50 km/h.
💡Durban to Cape Town
Durban and Cape Town are two major cities in South Africa, and the script uses the distance between them as an example to illustrate how to calculate the time it would take to travel from one city to the other at a given speed. This real-world context helps viewers understand how the concepts of speed, distance, and time can be applied practically.
💡Unit Conversion
Unit conversion is the process of converting a quantity from one unit to another. In the video, it is important to ensure that units are consistent when performing calculations, such as using kilometers for both distance and speed. The script highlights this by pointing out that 'if one of them was in hours and one of them was in minutes, then of course you would need to convert them to be the same units.'
💡Consistent Speed
Consistent speed is the assumption that the speed of an object remains constant throughout a given time period unless stated otherwise. This assumption is used in the video to simplify calculations and is mentioned in the script when it says 'we will assume that her speed is going to remain the same so now for this part, over here we know that she's still driving at the same speed.'
💡Morgan
Morgan is a personal name used in the video as an example for a hypothetical driver. The script uses Morgan to illustrate a scenario where distance and time are given, and the viewer is asked to calculate the distance covered. It serves as a narrative device to engage the viewer and make the content more relatable, as seen in 'Morgan drives 100 km in 80 minutes.'
Highlights

Introduction to the concept of rate in relation to speed, distance, and time.

Explanation of the relationship between speed, distance, and time using a triangle model for better understanding.

Formula for calculating speed: Speed equals distance divided by time (S = D/T).

Formula for calculating time: Time equals distance divided by speed (T = D/S).

Formula for calculating distance: Distance equals speed multiplied by time (D = S*T).

Emphasis on the importance of units when performing calculations, specifically kilometers per hour for speed.

Example calculation: A car drives 100 km in 2 hours, resulting in a speed of 50 km/h.

Method to find the time taken to travel a known distance at a given speed.

Example calculation: A vehicle travels from Durban to Cape Town at 120 km/h, covering a distance of 1650 km in 13.75 hours.

Explanation of how to calculate the distance a car travels given its speed and time.

Example calculation: A car travels 270 km at a speed of 60 km/h for 4.5 hours.

Use of the triangle model to solve for speed, time, or distance based on the given variables.

Example scenario: Nandy drives 250 km in 4 hours, calculating a speed of 62.5 km/h.

Comparison of speeds to determine the faster driver and the concept of constant speed in a given scenario.

Calculation of time taken to travel a distance of 520 km at a constant speed of 50 km/h, resulting in 10.4 hours.

Scenario involving Morgan driving 100 km in 80 minutes, emphasizing the need for unit consistency in calculations.

Final example calculation: Given a speed of 1.25 km/min and a time of 140 minutes, the distance traveled is 175 km.

Transcripts

Browse More Related Video

Speed, Distance and Time

Speed, Distance, Time - Corbettmaths

Maths Bitesize - The DST Triangle

The Speed, Distance and Time trick [No Ads]

Speed, distance and time

Distance Speed Time Word Problem Time to Overtake

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Speed CalculationDistance FormulaTime EquationEducational ContentMathematics LessonDriving SpeedKilometers per HourTravel TimeDistance TraveledSpeed UnitsLearning Techniques