Velocity - speed, distance and time - math lesson
TLDRIn this engaging video, the host delves into the fundamental concepts of speed calculations, which are essential for understanding how fast an object, such as a car, is moving. The video begins by establishing the basic formula for speed, which is distance divided by time, and explains that this can be expressed in various units like kilometers per hour or miles per hour. The host then illustrates how to calculate the speed of a car given a distance and time, using a simple example to demonstrate the process. Further, the video explores how to determine distance when speed and time are known, and how to calculate time when given speed and distance. The host emphasizes the importance of unit consistency when performing these calculations and provides a visual aid—a triangle—to help viewers understand the relationship between speed, distance, and time. The video concludes with a reminder to be cautious with unit conversions, especially when dealing with decimals in time measurements, ensuring that viewers can confidently tackle speed-related problems.
Takeaways
- 📐 **Speed Calculations**: The video focuses on understanding and calculating speed, which is defined as distance over time.
- 🚗 **Understanding Speed**: Speed is commonly understood in terms of road travel, such as kilometers per hour (km/h) or miles per hour (mph).
- 🌐 **Units of Speed**: Different regions use different units for speed, but the formula for speed (distance/time) remains the same regardless of the unit.
- 📉 **Speed Formula**: The formula for speed is speed = distance/time. This formula is fundamental for all speed-related calculations.
- ⏱️ **Time Calculations**: To find the time taken for a journey, use the formula time = distance/speed.
- 📏 **Distance Calculations**: To calculate the distance covered, the formula distance = speed × time is used.
- 🔄 **Unit Consistency**: It's crucial to ensure that units for speed, time, and distance are consistent when performing calculations.
- 🕒 **Time Conversion**: When calculating time, be aware of the conversion between different time units, such as minutes to hours.
- 🚫 **Unit Pitfalls**: Be cautious of unit mismatches, like mixing minutes with hours, which can lead to incorrect calculations.
- 📌 **Speed Limit Significance**: Speed limits are a common reference for understanding the concept of speed in everyday life.
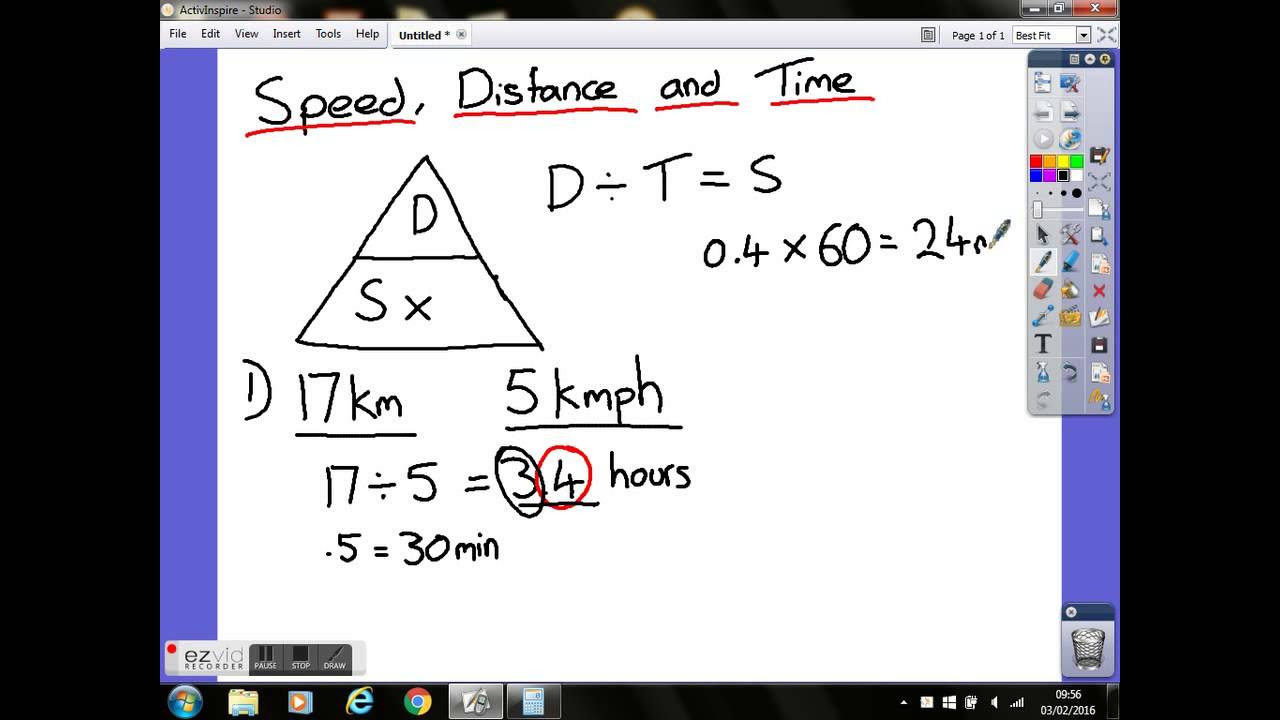
- ✍️ **Simple Formula Manipulation**: The video introduces a simple method for manipulating the speed formula by using a triangle diagram to represent the relationship between speed, time, and distance.
Q & A
What is the basic formula to calculate speed?
-The basic formula to calculate speed is speed = distance / time. This means that speed is the distance an object travels divided by the time it takes to travel that distance.
How is the speed limit sign related to the concept of speed?
-The speed limit sign is a common way to communicate the maximum speed at which vehicles should travel on a particular road. It is a practical application of the concept of speed, as it sets a limit on the rate at which vehicles can cover distance within a given time frame.
What units are commonly used to measure speed?
-Common units for measuring speed include kilometers per hour (km/h), miles per hour (mph), and meters per second (m/s). The choice of unit depends on the country and the context in which the speed is being measured.
How can you calculate the speed of a car if it travels a certain distance in a given time?
-To calculate the speed of a car, you would use the formula speed = distance / time. For example, if a car travels 120 kilometers in 5 hours, the speed would be 120 km / 5 hours = 24 km/h.
What is the relationship between speed, time, and distance when calculating time?
-When calculating time, the relationship is given by the formula time = distance / speed. This rearrangement of the basic speed formula allows you to find the time taken to travel a certain distance at a given speed.
How can you calculate the distance traveled at a given speed and time?
-To calculate the distance traveled, you use the formula distance = speed * time. By multiplying the speed (in the appropriate units per hour) by the time (in hours), you get the distance covered during that time period.
Why is it important to ensure units are consistent when performing calculations with speed, time, and distance?
-Consistent units are crucial for accurate calculations. If units are not the same, the resulting calculation will be incorrect. For instance, if time is given in minutes, it must be converted to hours to match the speed unit before calculating distance or time.
What is a common mistake made when converting time units in speed calculations?
-A common mistake is not properly converting time units, such as assuming that a decimal value represents a fraction of an hour without explicitly converting minutes into hours or vice versa.
How can the concept of a triangle be used to help remember the relationship between speed, time, and distance?
-Drawing a triangle with the formula speed = distance / time inside can help visualize the relationship. By covering parts of the formula with a thumb or another object, you can easily derive the other two formulas (time = distance / speed and distance = speed * time).
What is a pitfall to watch out for when calculating distance with mixed units?
-A pitfall to watch out for is ensuring that the units for both speed and time are consistent before performing the multiplication. For example, if the time is given in minutes, it needs to be converted to hours to match the speed unit, which is typically in units per hour.
How can understanding the relationship between speed, time, and distance be practically useful?
-Understanding the relationship between speed, time, and distance is practically useful in various real-life scenarios, such as calculating travel time for a journey, determining how long it will take to cover a certain distance at a specific speed, or figuring out how far you can travel within a given time frame.
Outlines
🚗 Introduction to Speed Calculations
The video begins with an introduction to the topic of speed calculations. The host explains that the video will cover how to calculate speed, distance, and time, using units like kilometers per hour (km/h) or miles per hour (mph). The host uses a simple drawing of a car to illustrate the concept of speed and mentions that speed is typically understood in terms of speed limit signs on roads. The fundamental formula for speed is introduced as speed equals distance over time, which can be applied to various units of measurement. The host also provides a basic example of calculating speed given a distance and time, emphasizing the importance of keeping units consistent.
🕒 Calculating Time and Distance with Speed
The second paragraph focuses on how to calculate time and distance when speed is known. The host demonstrates how to rearrange the speed formula to solve for time, which is distance over speed. An example is given where a distance of 1,000 miles is traveled at a speed of 60 miles per hour, resulting in a time calculation of 16.6 hours. The host warns viewers to be cautious with decimal values in time calculations, as they may represent fractions of an hour. The formula for distance is then shown as speed times time, and an example is provided where a speed of 100 kilometers per hour is multiplied by a time of 30 minutes (converted to 0.5 hours for consistency in units), resulting in a distance of 50 kilometers. The host emphasizes the importance of unit consistency when performing these calculations.
📝 Summary of Speed, Distance, and Time Calculations
The final paragraph serves as a summary of the key points covered in the video. The host reiterates the importance of understanding how to calculate distance over time measurements and how to manipulate the formulas to find speed, distance, or time when the other two variables are known. The host encourages viewers to apply the formulas and to be mindful of unit conversions when necessary. The video concludes with an invitation for any questions or comments, reminding viewers to take care and ending with a goodbye.
Mindmap
Keywords
💡Speed
💡Distance
💡Time
💡Formula
💡Units
💡Calculation
💡Speed Limit
💡Kilometers per hour (km/h)
💡Miles per hour (mph)
💡Artwork
💡Decimals
Highlights
The video discusses calculations involving speed, such as determining how fast something is moving in terms of kilometers per hour or miles per hour.
Speed is defined as distance over time, which can be remembered by the formula speed = distance/time.
The presenter uses a simple drawing of a car to illustrate the concept of speed in a way that is easily understood by most people.
Different units of speed are mentioned, such as kilometers per hour and miles per hour, with a note on the importance of understanding local units.
A method for calculating the speed of an object, such as a car, is demonstrated using a given distance and time.
An example calculation shows how to determine the speed of a car traveling 120 kilometers in 5 hours, resulting in 24 kilometers per hour.
The importance of matching units when performing calculations is emphasized to avoid errors.
A creative approach to rearranging the speed formula is introduced using a triangle diagram for visual aid.
The formula for calculating time when speed and distance are known is presented as time = distance/speed.
An example is given to calculate the time taken to travel a distance of 1,000 miles at a speed of 60 miles per hour, resulting in 16.6 hours.
The presenter cautions viewers to be aware of decimal places when dealing with time measurements to avoid misunderstandings.
The formula for calculating distance when speed and time are known is introduced as distance = speed * time.
An example calculation is provided to find the distance traveled at a speed of 100 kilometers per hour for 30 minutes, resulting in 50 kilometers.
The importance of converting time units to match before performing calculations is highlighted to ensure accuracy.
The video concludes with a reminder of the key formulas and the process of plugging in values to solve for speed, time, or distance.
The presenter encourages viewers to send any questions or comments, emphasizing the interactive nature of the educational content.
The video is designed to be accessible to viewers with little prior knowledge of speed calculations, making it inclusive and informative.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: