Big Picture: Derivatives
TLDRIn this video, the professor introduces the concept of derivatives in calculus, emphasizing the connection between rate of change and the slope of a function. By exploring the derivative of key functions like x^n, sine x, and e^x, the lecture reveals how these fundamental concepts are essential for understanding the behavior of more complex functions in science, engineering, and economics.
Takeaways
- 📚 The core concept of calculus involves understanding the relationship between two functions, such as distance and speed, and how they change relative to each other.
- 🚀 The analogy of an airplane climbing illustrates the need to recover lost speed information (the derivative) from known height information (the function).
- 📈 Calculus is used to find the slope (rate of change or speed) at a specific point, rather than just the total accumulation or average.
- 🎢 The lecture introduces the notation for derivatives created by Leibniz, emphasizing that calculus is about ideas rather than mere symbols.
- 🌟 Power functions (x to the nth power) have straightforward derivatives, with the rule that the derivative is x to the (n-1)th power.
- 📊 The derivative of the sine function is the cosine function, and vice versa, making them fundamental in understanding the behavior of these trigonometric functions.
- 📈 The derivative of the exponential function e to the x is the same as the original function, highlighting the unique relationship between the function and its rate of change.
- 🤔 The concept of a derivative provides a way to identify critical points on a curve, such as maximum and minimum values, by looking for where the slope is zero.
- 🔢 The process of finding the derivative involves taking limits, which allows for the transition from average rates of change to instantaneous rates.
- 🛤️ The lecture emphasizes the importance of understanding the slope at specific points for various functions, which is essential for applications in science, engineering, and economics.
- 🎥 The video is part of a series from MIT OpenCourseWare and Gilbert Strang, offering free and open access to educational content on calculus.
Q & A
What is the main focus of this calculus lecture?
-The main focus of this calculus lecture is to introduce and compute derivatives, emphasizing the connection between pairs of functions such as distance and speed, and the slope of a graph or a mountain.
How does the lecture illustrate the concept of speed and distance?
-The lecture illustrates the concept of speed and distance by using the analogy of an airplane's flight recorder. One recorder tracks the total distance (height) covered, while the other records the instantaneous speed at any given moment.
What is the significance of the slope in calculus?
-The slope in calculus is significant because it represents the rate of change of a function at a particular point. It is the central idea in differential calculus, which is used to analyze the behavior of functions and their rates of change.
How does the lecture explain the process of finding the slope of a function at a specific point?
-The lecture explains the process by considering a small change in the independent variable (delta x) and calculating the corresponding change in the dependent variable (delta y). The slope at a point is then found by taking the limit of the ratio delta y/delta x as delta x approaches zero.
What is the derivative of the function y = x^n, according to the lecture?
-The derivative of the function y = x^n is given by the formula y' = n * x^(n-1), where n is the exponent and x^(n-1) represents the power of x reduced by one.
What is the derivative of the sine function, as discussed in the lecture?
-The derivative of the sine function is the cosine function. In other words, if y = sin(x), then the derivative dy/dx = cos(x).
What is the significance of the point where the slope of a function is zero?
-The points where the slope of a function is zero are significant because they often represent extrema of the function, such as local maximum or minimum values. These points can be used to identify critical points or turning points on the curve.
How does the lecture use the concept of limits to find the slope at a point?
-The lecture uses the concept of limits by taking the ratio of the change in the dependent variable to the change in the independent variable and then finding the limit of this ratio as the change in the independent variable approaches zero. This limit provides the instantaneous slope at a specific point on the curve.
What is the significance of the function e^x in calculus?
-The function e^x is significant in calculus because its derivative is the same as the function itself. This means that the slope of the curve at any point is equal to the value of the function at that point, making it a fundamental function in the study of calculus.
What is the relationship between the slope of a function and the original function, as explained in the lecture?
-The relationship between the slope of a function and the original function is that the derivative, or the slope, represents the rate of change of the original function. It provides insights into how the function behaves, such as its increasing or decreasing nature, and can be used to find critical points and the behavior of the function at specific points.
How does the lecture demonstrate the process of finding the derivative of a function?
-The lecture demonstrates the process of finding the derivative by first identifying the original function, then considering a small change in the input (delta x) and the corresponding change in the output (delta y). It then calculates the average rate of change and takes the limit as delta x approaches zero to find the instantaneous rate of change, which is the derivative.
Outlines
📚 Introduction to Derivatives and the Concept of Slope
This paragraph introduces the concept of derivatives in calculus, emphasizing the connection between distance and speed, or height and slope, and how these relationships are central to understanding calculus. The professor uses the analogy of an airplane's flight recorder to explain the difference between tracking total distance (or height) and instantaneous speed, highlighting the importance of understanding what is happening 'at an instant.' The challenge presented is to recover the speed (or slope) from the total height information, setting the stage for the introduction of Leibniz's notation for the derivative and the process of deriving the slope of various functions.
📈 Deriving the Slope of Basic Functions
In this paragraph, the professor delves into the process of deriving the slope of basic functions, starting with the power function x to the nth. The explanation includes a visual representation of the graph of y equals x squared and how the slope changes as x varies. The concept of positive and negative exponents is introduced, and the derivative for these power functions is explained as another power of x, with the exponent reduced by one. The professor also touches on the importance of the sine and cosine functions, revealing that the derivative of sine x is cos x, and the derivative of cosine x is minus sine x, highlighting the utility and beauty of these relationships in calculus.
📊 Average vs Instantaneous Slope
This paragraph focuses on the distinction between average slope and instantaneous slope. The professor uses the example of the x squared curve to illustrate how average slope is calculated over a certain distance (delta x) and how this changes as the distance becomes smaller. The concept of limits is introduced as a method to find the instantaneous slope by letting delta x approach zero. The calculation shows that at x equals 0, the instantaneous slope is 0, which is a foundational step in understanding the behavior of functions at specific points.
🔢 Calculating Derivatives and the Role of Delta X
The professor continues the discussion on derivatives, focusing on the algebraic manipulation involved in calculating the slope at any given point on the curve y equals x squared. The concept of delta x, representing a small change in x, is used to calculate the change in y (delta y). The average slope is then found by dividing delta y by delta x. The process of simplifying this expression and taking the limit as delta x approaches zero to find the instantaneous slope is explained. The conclusion is that the derivative of x squared is 2x, which represents the slope function for this particular case.
📈 Graphical Representation of Derivatives
In this paragraph, the professor visually represents the concept of derivatives by graphing the derivative (slope function) alongside the original function (x squared). The derivative is shown as a linear function with a slope of 2x, starting at the origin and increasing linearly. The professor emphasizes the importance of visualizing the slope at different points on the curve and how the derivative function can be used to understand the behavior of the original function. The discussion also touches on the importance of understanding the maximum and minimum slopes, as well as the points of inflection, which are crucial for analyzing the behavior of functions in various applications.
🌟 The Sine Function and Its Derivative
The final paragraph of the script discusses the sine function and its derivative, the cosine function. The professor uses a graphical approach to illustrate the sine function and how the slope of the tangent line at any point on the curve corresponds to the cosine of that point. The discussion highlights the importance of understanding the rate of change and how it varies across the curve, with the derivative (cosine) providing a clear picture of this rate of change. The sine function's behavior is analyzed from the start, through its maximum and minimum points, and back to the start, emphasizing the cyclical nature of the function and the corresponding changes in the slope.
Mindmap
Keywords
💡Calculus
💡Derivatives
💡Slope
💡Function
💡Height and Distance
💡Speed
💡Flight Recorder
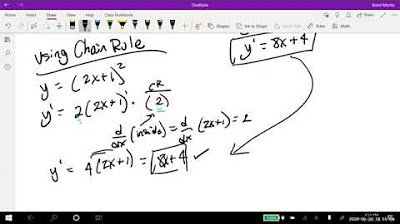
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Limits
Highlights
The introduction of the concept of derivatives in calculus, which are used to compute the slope or rate of change of a function at a specific point.
The analogy of an airplane climbing to explain the relationship between distance (height) and speed (slope), and how calculus helps to understand this relationship.
The explanation of how to recover the speed (derivative) from the total distance (function) traveled, even if the speed recorder is lost.
The historical note about Leibniz's notation for derivatives and its significance in calculus.
The concept of dividing distance by distance to find the slope, which is a fundamental idea in understanding derivatives.
The importance of understanding the difference between average slope and instantaneous slope, with calculus focusing on the latter.
The detailed calculation and explanation of the derivative of the function y = x^n, particularly focusing on the case when n = 2.
The visual representation of the slope of the function y = x^2 at different points, and how it changes as x varies.
The explanation of how the slope at the bottom of a curve (where the slope is 0) can be identified using calculus.
The process of calculating the derivative of a function by taking the limit as the interval approaches zero, demonstrated using the function y = x^2.
The introduction of the derivative rules (product rule, quotient rule, and chain rule) that are essential for more complex functions.
The explanation of the derivative of sine x as cosine x, and the derivative of cosine x as negative sine x, highlighting the relationship between the functions and their derivatives.
The introduction of the function e^x and its unique property that its derivative is the same as the function itself.
The practical application of calculus in identifying maximum and minimum points on a curve by looking at where the slope is zero.
The demonstration of how the graph of the derivative function (slope) relates to the original function, using the example of y = sine x and its derivative y = cosine x.
The emphasis on the importance of learning and understanding the basic functions and their derivatives, as they form the foundation for more complex applications in science, engineering, and economics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: