BusCalc 08 Derivative Basics
TLDRIn this educational video, the presenter delves into the fundamentals of derivatives, a pivotal concept in calculus. Starting with a review of how functions are represented graphically in the x-y plane, the video moves on to explain the derivative as the slope of the tangent line to a curve at any given point. The presenter then introduces several key rules for finding derivatives, including the constant rule (derivative of a constant function is zero) and the power rule (derivative of x^n is n*x^(n-1)). The video also covers the derivative of roots and rational exponents, emphasizing the importance of understanding these shortcuts for efficiency in calculus. Further, the homogeneity rule and additivity rules for derivatives of sums and differences are explained with examples. The presenter also highlights various notations used to represent derivatives, ensuring the audience is comfortable with the different mathematical conventions. The video concludes with a reminder of the practical applications of these rules and the significance of the derivative in understanding the rate of change.
Takeaways
- 📈 The derivative of a function, represented as f'(x), measures the slope of the tangent line to the curve of the function at a given point x.
- 📚 A function f(x) can be visually represented as a curve on the x-y plane, where x is the horizontal axis and f(x) (or y) is the vertical axis.
- 🔢 For a constant function, where k is any real number, the derivative is always zero because the slope of a horizontal line is zero.
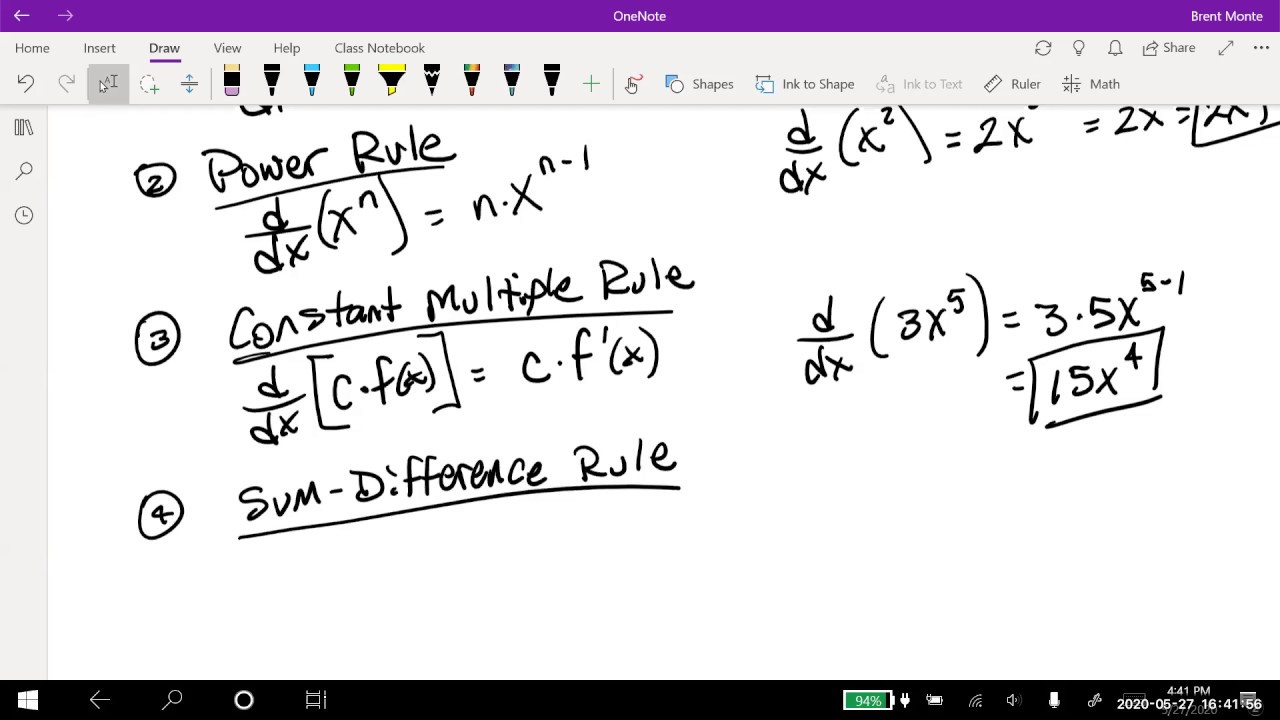
- ✋ The power rule states that the derivative of x raised to the power of n (where n is a real number) is n times x to the power of n minus 1.
- 👉 The square root of x can be expressed as x to the power of 1/2, and its derivative is 1/2 times x to the power of -1/2.
- 🤔 Rational exponents, such as the cube root of x (x^(1/3)), can be treated with the power rule by converting them to x raised to the power of the rational exponent.
- 📝 The derivative of a function multiplied by a constant (k), can be found by multiplying the constant with the derivative of the function, as per the homogeneity rule.
- 🔣 The additivity rules state that the derivative of a sum or difference of functions is the sum or difference of their derivatives.
- 📉 The derivative of a constant is always zero, as there is no change in the value of the function.
- 🔑 Different notations are used in mathematics to represent derivatives, such as f'(x), y', dy/dx, and df/dx, all of which mean the same thing.
- ✅ The additivity rule can be applied to express the derivative of a sum of functions as the sum of their individual derivatives, emphasizing the flexibility of derivative notation.
Q & A
What is the visual representation of a function in the x-y plane?
-A function, such as f(x), can be visually represented in the x-y plane with a curve. The horizontal axis represents x, and the vertical axis represents y. For example, if the function is f(x) = x^2, it can be represented by letting y = x^2 and plotting points that represent the function.
What does the derivative of a function represent?
-The derivative of a function, represented as f'(x), represents the slope of the tangent line to the curve of the function at any given point x.
What is the derivative of a constant function?
-The derivative of any constant function is zero. This is because a constant function has a horizontal line representing it, which means the slope, and hence the derivative, is zero everywhere.
What is the power rule for derivatives?
-The power rule for derivatives states that if you have a function of the form f(x) = x^n, where n is any real number, then the derivative f'(x) is n * x^(n-1). This means you bring down the exponent as a coefficient and reduce the exponent by one.
How can you represent the square root of x using the power rule?
-The square root of x can be represented as x to the power of 1/2. Using the power rule, the derivative of the square root of x would then be (1/2) * x^(-1/2), which can also be written as 1/(2√x).
What is the derivative of x to the power of -2?
-The derivative of x to the power of -2 can be found by applying the power rule. It is -2 * x^(-3), which can also be written as -2/x^3.
What does the additivity rule for derivatives state?
-The additivity rule for derivatives states that the derivative of a sum or difference of functions is the sum or difference of their derivatives. In other words, the derivative of f(x) = u(x) + v(x) is f'(x) = u'(x) + v'(x).
How can you use the homogeneity rule to find the derivative of a function multiplied by a constant?
-The homogeneity rule allows you to leave the constant multiplier alone when taking the derivative. For example, if you have a function f(x) = k * g(x), where k is a constant, the derivative f'(x) is simply k * g'(x).
What are the different notations used to represent derivatives?
-There are several notations used to represent derivatives: f'(x), y', dy/dx, d(y)/dx, and df/dx. All these notations represent the same concept of a derivative but are used in different contexts or preferences.
How does the script explain the derivative of a function involving a sum of terms?
-The script explains that when finding the derivative of a function that is a sum of terms, you can apply the additivity rule. This means you can find the derivative of each term separately and then sum them up. For instance, the derivative of f(x) = 3x^2 + 2x + 10 would be f'(x) = 6x + 2, ignoring the derivative of the constant term as it is zero.
What is the significance of understanding different notations for derivatives in mathematics?
-Understanding different notations for derivatives is important because it allows you to recognize and work with the concept of a derivative regardless of how it is presented. This is crucial for solving problems in calculus and other areas of mathematics where derivatives are used.
Outlines
📚 Derivative Basics and Power Rule Introduction
This paragraph introduces the concept of derivatives in calculus, mentioning that the video is likely covering section 11.5 of the textbook. It recaps that a function f(x) can be represented graphically as a curve on the x-y plane, and the derivative, denoted as f'(x), is the slope of the tangent line to the curve at any given point x. The paragraph also revisits the formula for the derivative from previous lessons and emphasizes the importance of understanding the connection between a function, its curve representation, and the derivative as the slope of the tangent line. It concludes by stating the intention to teach shortcuts or rules to simplify derivative calculations.
🔢 Derivative Power Rule and Constant Function Derivative
The paragraph explains the derivative power rule, which is a formula for finding the derivative of a function of the form x^n, where n is any real number. It states that the derivative of x^n is n*x^(n-1). The paragraph also covers the derivative of a constant function, which is always zero, as a constant function is represented by a horizontal line with a slope of zero. It provides examples to illustrate the power rule, such as the derivative of x^3 being 3x^2 and the derivative of x^7 being 7x^6. It also discusses how to handle roots and rational exponents by expressing them as powers of x and applying the power rule accordingly.
🧮 Derivative Calculations with Power Rule
This paragraph continues the discussion on derivatives, focusing on applying the power rule to various functions. It demonstrates how to find derivatives of functions like 1/x (x to the -1 power), x^(-2), and x^(1/2). The paragraph shows that the negative exponent in the power rule moves the term to the denominator, and it provides alternative ways to represent derivatives, such as using square roots or cube roots. It also emphasizes the importance of recognizing equivalent forms of the same mathematical expression and provides additional examples to solidify the understanding of the power rule.
📝 Homogeneity and Additivity Rules in Derivatives
The paragraph introduces two more rules for simplifying derivative calculations: the homogeneity rule and the additivity rules. The homogeneity rule states that when a function is multiplied by a constant, the constant can be factored out when taking the derivative. The additivity rules state that the derivative of a sum or difference of functions is the sum or difference of their derivatives, respectively. The paragraph provides examples to illustrate these rules, such as finding the derivative of 7x^5 and -42√x, and explains how to apply these rules to more complex functions by breaking them down into simpler components.
🔄 Applying Additivity and Power Rules to Polynomial Functions
This paragraph applies the previously discussed rules to find the derivatives of polynomial functions. It shows how to use the power rule, homogeneity rule, and additivity rules to find the derivative of a function like f(x) = 3x^2 + 2x + 10. The paragraph demonstrates that the derivative of each term can be calculated separately and then combined, and it also reminds the viewer that the derivative of a constant is zero. It concludes by writing the derivative in a simplified form, emphasizing the importance of committing the basic derivative rules to memory for their usefulness throughout the course.
📝 Derivative Notation and Additivity Rule Summary
The final paragraph emphasizes the various notations used in mathematics to represent derivatives, such as f'(x), y', dy/dx, d/dx, and the use of ' with respect to x'. It stresses the importance of being familiar with these notations as they all represent the same concept. The paragraph also revisits the additivity rule, showing different ways to express it, and reiterates the homogeneity rule, clarifying that constant factors can be pulled out of the derivative operator. The video concludes with a reminder to understand these concepts and notations as they will be frequently used.
Mindmap
Keywords
💡Derivative
💡Function
💡Tangent Line
💡Constant Function
💡Power Rule
💡Square Root
💡Homogeneity Rule
💡Additivity Rules
💡Notation
💡Chain Rule
💡Exponent
Highlights
Derivatives are the slope of the tangent line to a curve at any given point x.
A function f(x) can be represented in the x-y plane with a curve.
The derivative of a constant function is always zero, as its slope is zero everywhere.
The power rule for derivatives states that the derivative of x^n is n*x^(n-1).
Rational exponents can be expressed as roots, such as the square root of x being x^(1/2).
Derivatives of functions involving roots can be found using the power rule by rewriting the root as a rational exponent.
The homogeneity rule allows you to take a constant out of the derivative operator, applying it after calculating the derivative of the function.
Additivity rules state that the derivative of a sum or difference of functions is the sum or difference of their derivatives.
The derivative of x to any power can be found using the power rule, simplifying the process of finding derivatives.
Different notations for derivatives, such as f'(x), y', dy/dx, and d/dx [f(x)], all represent the same concept.
The derivative of a sum of functions can be found by taking the derivative of each function individually and then summing them.
The derivative of a constant value is always zero, as there is no change in the value.
Understanding and memorizing the basic derivative rules is crucial for solving calculus problems efficiently.
Different notations for derivatives should be recognized and understood to solve problems presented in various formats.
The video provides multiple examples of using the power rule, homogeneity rule, and additivity rules to find derivatives.
Shortcuts and rules for derivatives make the process of finding derivatives much easier and less time-consuming.
The video emphasizes the importance of being familiar with various notations and rules to successfully approach calculus problems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: