01 - Basic Derivatives in Calculus, Part 1 - Learn what a Derivative is and how to Solve Them.
TLDRThe video script is an educational tutorial focusing on derivatives, a fundamental concept in calculus. The instructor emphasizes the importance of understanding how to calculate derivatives, which are used to determine the rate of change of a function. The script introduces the concept of a derivative as the slope of the tangent line to a curve at a given point, illustrating this with the example of a parabola (f(x) = x^2). The instructor also covers basic rules for differentiation, such as the derivative of a constant being zero, the power rule for functions of the form x^n (where the derivative is n*x^(n-1)), and the rules for handling constants multiplied to functions and sums of functions. The goal is to equip students with the skills to tackle a variety of derivative problems, which are not only essential for calculus but also applicable in fields like physics. The script assures that with practice, students will become proficient in differentiating any function they encounter.
Takeaways
- 📚 The core principle of this DVD course is to focus on understanding and calculating derivatives, which is a fundamental concept in Calculus 1.
- 🔍 The course aims to provide a deep dive into derivatives, offering a wealth of practice problems to build problem-solving skills and prepare for exams.
- 📈 Derivatives are practically used to determine the rate of change of a function with respect to another variable, commonly time.
- 📈 The derivative of a function at a point represents the slope of the tangent line to the function at that point, indicating how fast the function is changing.
- 📘 The first derivative of a function f(x) is denoted as f'(x) or df/dx, and it represents the slope of the function at any given point.
- 🔢 A constant function (a horizontal line) has a derivative of zero because its rate of change (slope) is zero everywhere.
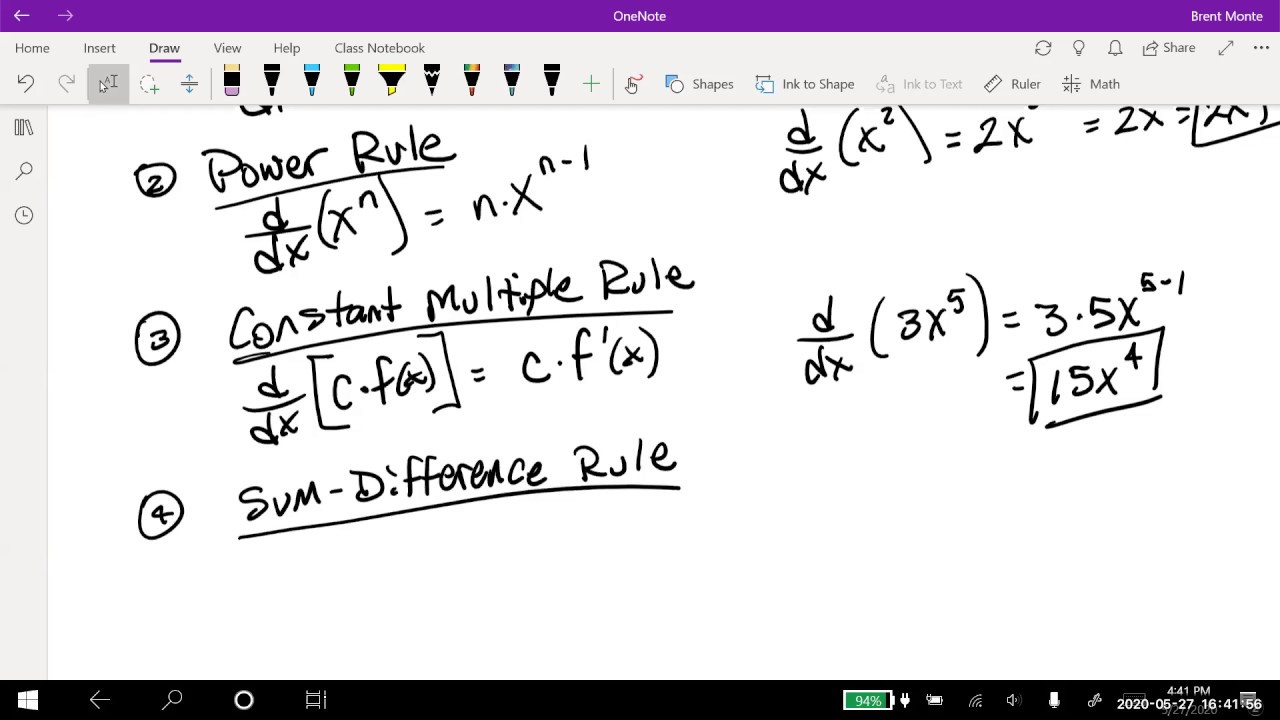
- ↗️ When taking the derivative of a function of the form x^n, where n is the exponent, the process involves bringing the exponent in front, multiplying by x, and then reducing the exponent by one.
- 🚫 If there's a constant multiplied by a function, the constant comes out in front of the derivative of the function.
- 🤝 The derivative of a sum of functions is found by taking the derivative of each individual function and then summing those derivatives.
- 📊 The graphical representation of a derivative (f'(x)) is a way to visualize the rate of change or slope of the original function (f(x)) at every point.
- 📈 Understanding and practicing the basic rules of differentiation is essential for success in calculus, as it builds a strong foundation for tackling more complex problems.
Q & A
What is the primary focus of the DVD course mentioned in the transcript?
-The primary focus of the DVD course is to provide extra help with derivatives, which is one of the core principles of Calculus 1.
What does the instructor claim the DVD course will serve as for students?
-The instructor claims that the DVD course will serve as a vault of pre-worked problems, which can help students understand how to do their homework and also serve as a review tool for exams and tests.
What is the practical meaning of a derivative?
-The practical meaning of a derivative is that it tells you how fast something is changing. It represents the rate of change of a function at a particular point.
How is the concept of a derivative introduced in a calculus book?
-In a calculus book, the concept of a derivative is introduced in terms of a limit, which is the actual mathematical definition of a derivative.
What does the instructor suggest is the best way to learn how to take derivatives?
-The instructor suggests that the best way to learn how to take derivatives is by working through a lot of problems, which helps to sharpen skills and provides practice for tests and homework.
What is the first step in taking the derivative of a function?
-The first step in taking the derivative of a function is to identify the type of function or term you are dealing with and apply the appropriate rule for differentiation.
What is the rule for differentiating a function of the form f(x) = x^n, where n is a constant?
-The rule for differentiating a function of the form f(x) = x^n is to bring the exponent n down in front of x, and then subtract 1 from the exponent, resulting in f'(x) = n*x^(n-1).
How does the instructor describe the process of taking the derivative of a constant function?
-The instructor describes the process of taking the derivative of a constant function as straightforward, stating that the derivative of a constant function is always zero, since the slope of a constant (horizontal) line is zero.
What is the notation used to represent the first derivative of a function f(x) with respect to x?
-The notation used to represent the first derivative of a function f(x) with respect to x can be either f'(x) or d(f(x))/dx, both of which mean the same thing.
How does the instructor explain the process of taking the derivative of a sum of functions?
-The instructor explains that to take the derivative of a sum of functions, you take the derivative of each individual function and then add the results together.
What is the purpose of reviewing basic derivative rules and working through problems in the DVD course?
-The purpose of reviewing basic derivative rules and working through problems is to build students' skills in differentiation, ensuring they can apply these rules to a variety of functions and problems with confidence.
Outlines
📚 Introduction to Calculus 1 and Derivatives
The video script introduces the Calculus 1 DVD course focusing on derivatives, a core principle in calculus. The course aims to provide in-depth understanding and practice with derivatives, offering a wealth of solved problems to help students with homework and exam preparation. The presenter mentions an existing Calculus 1 Tutor course and suggests watching it for foundational knowledge before diving deeper into derivatives. The script emphasizes the importance of practice and understanding derivatives as a measure of rate of change, with real-world applications in physics and other fields.
🔍 Understanding the Practical Meaning of Derivatives
The paragraph delves into the concept of a derivative, emphasizing its practical significance as a measure of how quickly something changes. Using everyday examples like speed and temperature change, the script connects the derivative to the rate of change with respect to time. The mathematical representation of a derivative is introduced as the slope of a function at a specific point. The paragraph also explains the tangent line to a curve at a point, which represents the instantaneous rate of change at that point. The discussion aims to provide a concrete understanding of derivatives before moving on to differentiation methods.
📈 Derivatives and the Tangent Line Concept
This section of the script explores the graphical representation of derivatives, specifically how the slope of a tangent line to a curve at any point represents the derivative at that point. The discussion covers how the slope varies along the curve, with the derivative being higher where the curve is steeper and lower where it's more gradual. The concept of a horizontal tangent line, indicating a slope of zero, is also explained, showing that at the vertex of a parabola, the derivative is zero. The paragraph concludes with a visual representation of the derivative as a function that varies with changes in slope across the curve.
📘 Derivative as a Function's Slope Representation
The script explains that the derivative of a function is a separate function that represents the slope of the original function at every point. It emphasizes the importance of understanding how to calculate derivatives and how plotting the derivative can provide insight into the behavior of the original function. The paragraph introduces the notation for derivatives, including the common representations f'(x) and d/dx[f(x)]. It also establishes that the derivative function can be evaluated at any point to find the slope of the original function at that point.
📝 Basic Rules of Differentiation
The paragraph outlines the fundamental rules for taking derivatives, starting with the rule that the derivative of a constant is always zero. It then presents the power rule for functions of the form x^n, where the derivative is n*x^(n-1). The script also addresses what happens when a function is multiplied by a constant or when there's a sum of multiple functions. The importance of practice in mastering these rules is highlighted, as understanding the theory is not enough to ensure proficiency in calculating derivatives.
🔢 Applying Basic Rules to Simple Functions
The script provides examples of applying the basic rules of differentiation to simple functions. It demonstrates how to find the derivative of x raised to a power, such as x^4 and x^5, using the power rule. The process is then extended to a function that is a sum of two terms, like x^2 + x, by taking the derivative of each term separately and adding the results. The explanation clarifies that anything to the power of zero is equal to one, simplifying the expression of derivatives. The paragraph emphasizes that with practice, these derivative calculations will become second nature.
Mindmap
Keywords
💡Derivative
💡Rate of Change
💡Limit
💡Slope
💡Function
💡Tangent Line
💡Calculus 1 Tutor
💡
💡Differentiation Methods
💡Constant Function
💡Power Rule
💡Sum of Functions
Highlights
The DVD course focuses on the core principle of calculus, specifically how to properly take derivatives.
The course provides a repository of pre-worked problems to help students with homework and exam preparation.
The instructor already has a popular Calculus 1 tutor DVD course, which this extra help builds upon.
The material covered is about half of Calculus 1, with an emphasis on working through a variety of problems.
Derivatives are introduced as a practical concept, indicating how fast something changes.
The rate of change is a key concept, with examples such as velocity being the derivative of position.
The derivative of a function at any given point is represented by the slope of the tangent line to the function at that point.
The instructor uses a parabola (f(x) = x^2) to illustrate the concept of derivatives graphically.
The derivative of x squared is shown to be 2x, representing the slope of the tangent line at every point on the curve.
The course teaches how to calculate derivatives mathematically, not just graphically.
Differentiation methods will be covered in every section of the course, aiming to make students comfortable with derivatives of any function.
The derivative of a constant function is always zero, as there is no change in the function's value.
The power rule for derivatives states that for a function f(x) = x^n, the derivative f'(x) = n*x^(n-1).
When a constant is multiplied by a function, the constant can be factored out when taking the derivative.
The sum of two functions' derivatives is equal to the sum of their individual derivatives.
The course emphasizes the importance of practice in mastering the skill of taking derivatives.
The instructor provides a clear, step-by-step approach to understanding and calculating derivatives.
The course is designed to be accessible, with the aim of making complex calculus concepts easy to grasp.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: