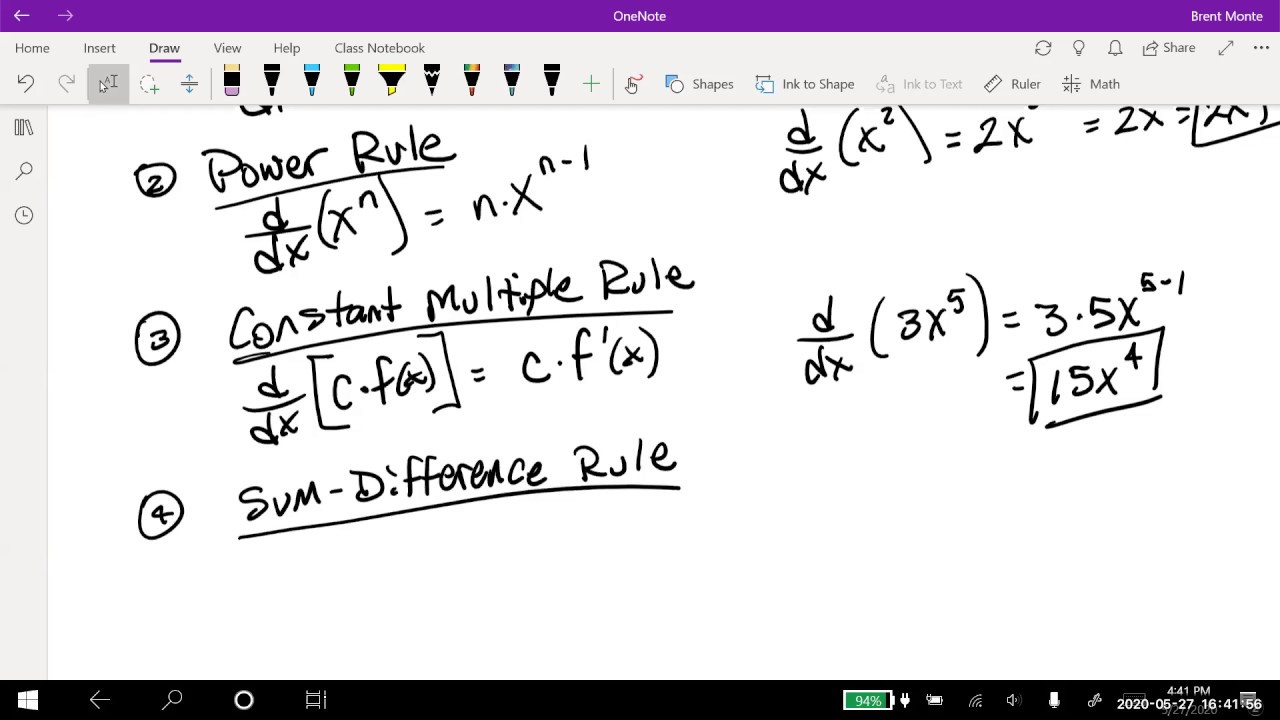
Is dy/dx a fraction?
TLDRThe video script discusses the concept of fractions and rational numbers, differentiating them from the mathematical notation of derivatives, specifically dy/dx. It uses the analogy of pizza slices to explain fractions and contrasts this with the concept of a derivative, which is the slope of a tangent line and not a fraction. The script clarifies that while dy/dx resembles a fraction in form, it represents a limit of a ratio as Δx approaches zero, and thus, is not a fraction. The explanation is engaging and uses visual examples to clarify the concepts.
Takeaways
- 🍕 Fractions are parts of a whole, like slices of pizza representing a portion.
- 📝 The definition of a fraction is simple: it represents a part of a whole, typically using two integers where the denominator cannot be zero.
- 🌟 Rational numbers are fractions where both the numerator and the denominator are integers, including negative integers.
- 🅾️ Irrational numbers, such as 2/π, are not considered rational because they involve non-integer values like π.
- 📊 The concept of dy/dx in calculus is not a fraction, even though it may resemble one in form. It represents the slope of the tangent line at a specific point on a curve.
- 🔄 The derivative (dy/dx) is defined as the limit of the ratio Δy/Δx as Δx approaches zero, which is different from the concept of a fraction.
- 🏫 Understanding the difference between fractions, ratios, and the derivative is crucial for grasping mathematical concepts.
- 📈 In ratios, the top number represents one part, while the bottom number represents another part, and they are often written in fraction notation.
- 🤔 While ratios can be expressed using fraction notation, they do not represent parts of a whole, and thus are not fractions.
- 🌐 The distinction between fractions and ratios is important, especially when dealing with mathematical operations and interpretations.
- 🧠 Grasping the concept of the derivative as a ratio, but not a fraction, is key to understanding calculus and the behavior of functions.
Q & A
What is the basic definition of a fraction?
-A fraction is a part of a whole, representing a division of a unit into equal parts.
How does the concept of a pizza being divided into slices illustrate the idea of a fraction?
-When a pizza is cut into slices and a certain number of slices are taken, the fraction represents the ratio of the taken slices to the total number of slices, such as three out of eight slices.
What is the difference between a rational number and an irrational number?
-A rational number can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero. An irrational number, on the other hand, cannot be expressed as a simple fraction; it's a non-repeating, non-terminating decimal, such as the number pi.
Why is dy/dx not considered a fraction despite its similar appearance?
-Although dy/dx looks like a fraction, it represents the rate of change or the slope of the tangent line at a particular point on a curve, not a part of a whole. The 'dx' in dy/dx does not represent a whole that 'dy' is a part of, which is a requirement for something to be considered a fraction.
What is the limit process involved in finding the derivative, and how does it relate to dy/dx?
-The limit process involved in finding the derivative takes the limit as Δx approaches 0 of the ratio Δy/Δx. This gives the instantaneous rate of change at a specific point, which is the slope of the tangent line at that point. This process is what makes dy/dx a rate of change rather than a fraction representing a part of a whole.
How can the concept of ratios be confused with fractions?
-Ratios can be written using fraction notation, like 20:600 written as 20/600, which might seem like a fraction. However, ratios represent the relative sizes of two quantities, not a part of a whole, so they are not fractions.
What is the significance of the derivative (dy/dx) in calculus?
-The derivative, represented as dy/dx, is a fundamental concept in calculus that describes how a function changes as its input changes. It is used to analyze the rate of change, the slope of curves, and to find critical points and maximum or minimum values of functions.
How does the concept of an improper fraction differ from a typical fraction?
-An improper fraction is a fraction where the numerator is equal to or greater than the denominator, such as 5/3. A typical fraction has a numerator that is less than the denominator. While both are technically fractions, improper fractions can be simplified to a whole number or a mixed number.
What is the relationship between dy/dx and the slope of a secant line?
-The expression dy/dx represents the slope of the tangent line at a specific point on a curve, whereas the slope of a secant line is based on two points and can vary depending on the chosen points. As the points used to calculate the secant line slope get closer together, the secant line approaches the tangent line, and their slopes become more similar.
How can the notation of dy/dx be simplified using the derivative?
-The notation dy/dx can be simplified by recognizing that the derivative, denoted as f'(x) or dy/dx, represents the slope of the tangent line at a point. Thus, dy/dx can be rewritten as f'(x), and when considering a specific point x=a, it can be further simplified to f'(a), which gives the slope at that point.
What is the practical application of understanding the difference between fractions, ratios, and dy/dx?
-Understanding the difference between fractions, ratios, and dy/dx is crucial for accurate mathematical communication and problem-solving. It helps to avoid confusion in calculations, correctly interpret results, and apply mathematical concepts appropriately in various fields such as physics, engineering, and economics.
Outlines
🍕 Understanding Fractions and Rational Numbers
This paragraph introduces the concept of fractions using the analogy of pizza slices to explain how fractions represent parts of a whole. It further distinguishes between fractions and mathematical expressions like dy/dx by clarifying that while dy/dx may resemble a fraction in form, it is not actually a fraction because it does not represent a part of a whole. The explanation extends to rational numbers, emphasizing that for a number to be considered rational, both the numerator and the denominator must be integers, and the denominator cannot be zero. The paragraph also addresses the difference between rational and irrational numbers, using the example of two over pi to illustrate that the latter is not a rational number.
📐 Exploring the Concept of Derivatives and Tangent Lines
The second paragraph delves into the concept of derivatives and tangent lines in calculus. It begins by illustrating how to find the slope of a secant line using two points on a curve, represented by (x1, y1) and (x2, y2). The paragraph then explains the difference between the slope of a secant line and the slope of a tangent line, which is the derivative of the function at a specific point. The tangent line's slope is denoted as the function's derivative evaluated at x1. The explanation includes a visual description of drawing the tangent line and the process of finding the derivative as the limit of the ratio of the change in y to the change in x as x approaches zero. The summary highlights the key points of understanding the relationship between ratios, derivatives, and fractions, and clarifies that while dy/dx may look and function like a fraction, it is technically not a fraction.
🤔 Clarifying the Distinction Between Fractions and Ratios
This paragraph focuses on clarifying the distinction between fractions and ratios, emphasizing that while they may appear similar and can be notated in the same way, they have different meanings. It reiterates that a fraction represents a part of a whole, whereas a ratio is a comparison of two quantities. The explanation includes an example of a ratio involving students and integrals, and how it can be written in fraction notation, but it is not a fraction because it does not represent a part of a whole. The paragraph reinforces the idea that although ratios can be expressed using fraction notation, they are not fractions, and neither is dy/dx in the context of derivatives. The summary underscores the importance of understanding the definitions and distinctions between these mathematical concepts.
Mindmap
Keywords
💡fraction
💡rational number
💡irrational number
💡derivative
💡limit
💡slope
💡tangent line
💡secant line
💡analogies
💡notation
💡calculus
💡dy/dx
Highlights
Introduces a unique analogy comparing the concept of fractions to slicing a pizza into parts.
Explores the definition of a fraction as a part of a whole through a practical example.
Differentiates between rational numbers and fractions by using the example of π (pi).
Clarifies that a fraction must involve integers in both numerator and denominator to be considered a rational number.
Addresses common misconceptions about fractions and rational numbers.
Introduces the concept of dy/dx in calculus, distinguishing it from simple fractions.
Explains the slope of secant lines versus the slope of tangent lines in calculus.
Demonstrates the use of limits to define the derivative dy/dx.
Illustrates how dy/dx is not a fraction by emphasizing the difference in conceptual understanding.
Uses the analogy of student to homework ratio to explain ratios versus fractions.
Explains that while ratios can resemble fractions, they do not always represent a part of a whole.
Introduces the concept of differential equations in the context of ratios and fractions.
Clarifies the distinction between a mathematical fraction and ratios that do not represent parts of wholes.
Concludes with the nuanced view that dy/dx behaves like a fraction in manipulation but fundamentally is not one.
Uses a creative analogy comparing someone who looks like Pikachu to the essence of dy/dx, emphasizing appearances versus intrinsic nature.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: