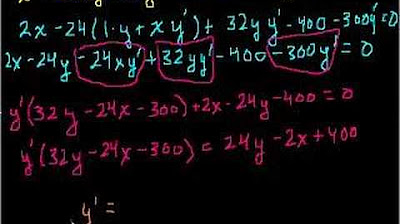Implicit Differentiation Examples
TLDRThe video script presents a comprehensive guide to implicit differentiation, emphasizing the application of the chain rule and other fundamental differentiation rules. The presenter illustrates the process through two examples, highlighting the importance of not overlooking the derivative of a constant, which is zero. The first example demonstrates finding the derivative dy/dx for a given relation without explicitly solving for y, while the second example focuses on determining the equation of a tangent line at a specific point on a curve. The script advises on simplifying the algebra by substituting values immediately after differentiation rather than solving for dy/dx first. The video aims to clarify that differentiation, while requiring attention to detail, is not inherently difficult and offers practical tips for tackling such problems.
Takeaways
- 📘 Implicit differentiation is a technique that applies the chain rule and other known differentiation rules to equations where y is implicitly defined as a function of x.
- 🔑 When differentiating both sides of an equation with respect to x, remember that the derivative of a constant is zero, which simplifies the equation.
- 🔍 Use the chain rule for terms involving y, as y is a function of x, leading to expressions like 3y^2 * (dy/dx) when differentiating y^3.
- ✍️ After differentiating, rearrange the terms to isolate (dy/dx) on one side of the equation to solve for the derivative.
- 🧐 Be cautious with negative signs during the differentiation process, as they can be easily mishandled, especially when distributing them across terms.
- 📐 For finding the equation of a tangent line, substitute the given point into the differentiated equation to find the slope (dy/dx) at that point.
- 📈 The point-slope form of a line, y - y0 = m(x - x0), is used to find the equation of the tangent line once the slope (m) is known.
- 🤔 Implicit differentiation can be more complex when there are variables and products on both sides of the equation, requiring careful application of the product rule.
- 📉 When solving for dy/dx, it's often easier to substitute values immediately after differentiation rather than solving for dy/dx first and then substituting.
- 📋 Always take the derivative of both sides of the equation, which means differentiating constants can lead to zero and simplify the equation.
- 📝 It's important to keep track of the chain rule application when differentiating terms with y in them, as it will always include a factor of dy/dx.
- 🎯 For multiple-choice questions, be aware that negatives and their distribution can sometimes be a source of error, so double-check your work.
Q & A
What is the main topic of the video?
-The main topic of the video is implicit differentiation, which involves applying the chain rule and other differentiation rules to find derivatives in situations where explicit differentiation is difficult or not possible.
Why is it important not to forget that the derivative of a constant is zero?
-It is important because forgetting this can make the derivative look more complicated than it actually is, and it can lead to incorrect results when solving for dy/dx.
What is the chain rule and how is it used in implicit differentiation?
-The chain rule is a fundamental principle in calculus that allows us to differentiate composite functions. In implicit differentiation, it is used when differentiating terms involving y (which is a function of x), resulting in the expression dy/dx being included in the derivative.
How does the video demonstrate the process of solving for dy/dx using implicit differentiation?
-The video demonstrates this by taking the derivative of both sides of a given equation with respect to x, then solving for dy/dx by rearranging terms and factoring out dy/dx.
What is a common mistake made when differentiating terms involving y?
-A common mistake is to forget to apply the chain rule, which leads to not including dy/dx in the derivative of terms that are functions of x.
Why is it recommended to substitute the point directly after taking the derivative, rather than solving for dy/dx first?
-Substituting the point directly after taking the derivative simplifies the algebra and makes it easier to solve for dy/dx, as it reduces the complexity of the expression before plugging in the values.
What is the point-slope form of the equation of a line?
-The point-slope form of the equation of a line is given by y - y0 = m(x - x0), where m is the slope of the line and (x0, y0) is a point on the line.
How does the video approach finding the equation of the tangent line at a specific point?
-The video finds the derivative at the specific point, substitutes the coordinates of the point into the derivative, and then uses the point-slope form to find the equation of the tangent line.
null
-null
What is the significance of the negative sign in the derivative of the first example?
-The negative sign in the derivative of the first example is distributed to the terms in the denominator, which is a common occurrence when dealing with differentiation. It's important to correctly distribute the negative sign to avoid errors in the final solution.
How does the video handle the second example where there is a product and variables on both sides?
-The video uses the product rule and the chain rule to differentiate both sides of the equation. It then simplifies the expression by substituting the given point to find the slope of the tangent line at that point.
What is the final answer for dy/dx in the second example after substituting the point (2, -2)?
-After substituting the point (2, -2) into the derivative, the video finds that dy/dx is 76, which is used to determine the equation of the tangent line at that point.
What is the general advice given in the video for dealing with implicit differentiation problems?
-The video advises to take the derivative of both sides of the equation, remember that the derivative of a constant is zero, and when finding the derivative at a particular point, it's easier to plug in the point after taking the derivative rather than solving for dy/dx first.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, which is a method used when it is difficult to explicitly solve for y in terms of x. The speaker emphasizes the importance of using the chain rule and other differentiation rules that the audience is already familiar with. The paragraph sets the stage for two examples that will be worked through to illustrate the process of implicit differentiation.
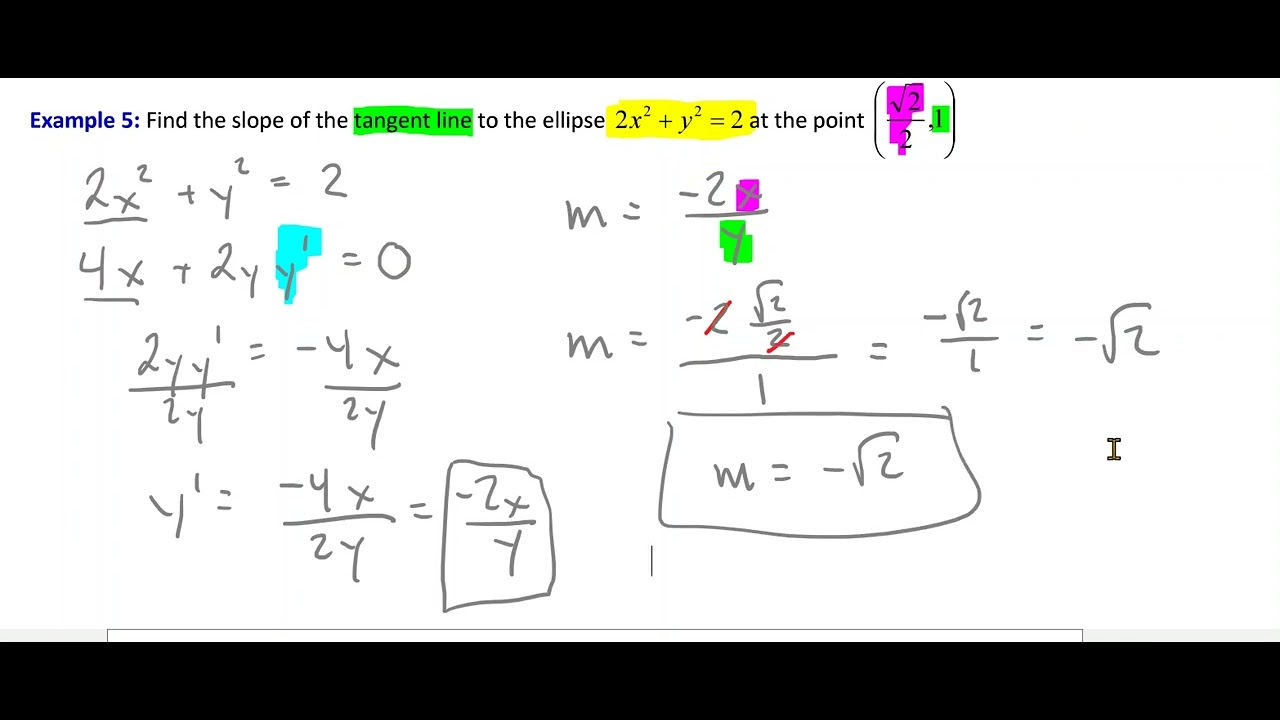
🔍 Implicit Differentiation: First Example
The first example demonstrates how to use implicit differentiation to find the derivative dy/dx for a given relation where solving for y directly is challenging. The process involves differentiating both sides of the equation with respect to x, applying the chain rule for terms involving y, and remembering that the derivative of a constant is zero. The example concludes with solving for dy/dx, which in this case results in -2x/(3y^2 - 2), and a caution about the common mistake of incorrectly distributing negatives in the equation.
📐 Finding the Tangent Line: Second Example
The second example focuses on finding the equation of the tangent line to a relation at a specific point (2, -2). The process is more complex due to the presence of variables on both sides and a product term. The speaker explains the application of the product rule and the chain rule, and then simplifies the equation by substituting the given point. This substitution leads to a straightforward algebraic problem, which is solved to find dy/dx = 76. The paragraph concludes with the equation of the tangent line in point-slope form, emphasizing the ease of plugging in values after differentiation rather than solving for dy/dx first.
Mindmap
Keywords
💡Implicit Differentiation
💡Chain Rule
💡Derivative of a Constant
💡Tangent Line
💡Point-Slope Form
💡Product Rule
💡Substitution
💡
💡Differentiation
💡Slope
💡Equation of a Line
💡Differential Equation
Highlights
The video is about implicit differentiation, which is an application of the chain rule and other known differentiation rules.
Implicit differentiation is used when it is difficult to solve for y directly.
The derivative of both sides of an equation is taken with respect to x in implicit differentiation.
It is important to remember that the derivative of a constant is zero, which is a common oversight.
The chain rule is applied when differentiating terms that include y as a function of x.
The video demonstrates solving for dy/dx by rearranging terms and factoring out dy/dx.
Negatives often get distributed and can complicate the derivative if not handled correctly.
The video presents a second example involving finding the tangent line at a specific point.
When finding the tangent line, it is simpler to substitute the point after taking the derivative rather than solving for dy/dx first.
The video emphasizes the importance of not forgetting to take the derivative of both sides of the equation.
The derivative of a constant term will often result in zero, which simplifies the equation.
The video provides a step-by-step guide on how to apply implicit differentiation to find dy/dx.
The process of solving for dy/dx involves moving terms involving dy/dx to one side and constants to the other.
The final answer for dy/dx in the second example is simplified to 76.
The video concludes with the equation of the tangent line in point-slope form.
The presenter advises to plug in the point of interest immediately after differentiating to simplify the process.
The video is aimed at helping viewers understand the process of implicit differentiation and its application in finding tangent lines.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: