Polynomial derivatives [IB Maths AI SL/HL]
TLDRThe script is a comprehensive guide on how to calculate derivatives of polynomials, a fundamental concept in calculus. It emphasizes the importance of understanding derivatives by hand, as it's key to grasping calculus. The presenter uses the analogy of 'Amazon Prime' to explain the notation of derivatives and offers a clear rule for differentiating terms with exponents: the exponent becomes the coefficient and decreases by one. The script walks through various examples, including terms with constants, negative exponents, and fractions, simplifying them into a 'calculus-friendly' form. It also touches on the concept of a derivative of a constant being zero and illustrates how to deal with sums of terms by differentiating each part separately. The guide is instructional, engaging, and filled with practical tips to help users master the concept of derivatives, which is not only essential for calculus but also widely applicable in fields like physics.
Takeaways
- 📚 The derivative of a polynomial can be found by applying the power rule, which states that the derivative of x^n is n*x^(n-1).
- 🔑 When writing derivatives, it's common to use the notation f'(x) or df/dx, which represents the derivative of f with respect to x.
- 🎮 For a more 'calculus-friendly' expression, rewrite terms with negative exponents as positive exponents with the base x, such as 1/x^2 becoming x^(-2).
- 🧩 When taking the derivative of a sum of terms, you can find the derivative of each term separately and then combine them.
- ✅ The derivative of a constant is zero, which means constants disappear when taking the derivative.
- 📉 When the exponent of x is 1, the x disappears from the derivative, as seen when going from x^3 to x^2 or from x^2 to x.
- 🤔 To find the gradient of a tangent line at a point without using two points or drawing the line, you can use the derivative at that point.
- 📐 The process of finding derivatives can be seen as a game with rules, which helps in understanding and memorizing the process.
- 📈 The derivative of a function at a specific point gives you the slope of the tangent line to the function at that point.
- 📋 It's important to remember that when taking the derivative of a term with a number in front (e.g., 4x^3), the number is treated as a coefficient and is multiplied by the derivative of the variable part.
- 🔍 For terms with x in the denominator, like fractions, it's beneficial to rewrite them with x in the numerator with a negative exponent before differentiating.
Q & A
What is the derivative of a polynomial?
-The derivative of a polynomial can be found by applying the power rule, which states that the derivative of x to the power of n is n times x to the power of n minus 1.
How do you represent the derivative of a function y?
-The derivative of a function y can be represented as y prime (y'), f prime of x (f'(x)), or dy/dx.
What is the purpose of learning to find the derivative by hand?
-Learning to find the derivative by hand is important because it is key to understanding calculus, and it allows you to find the gradient of a tangent at any point without needing to use two points or draw the tangent line.
What is the rule for differentiating a term with a negative exponent?
-When differentiating a term with a negative exponent, you bring the exponent in front and decrease it by one. For example, the derivative of x to the power of -n would be -n times x to the power of -n minus 1.
How do you deal with a constant term when differentiating?
-The derivative of a constant term is zero. Constants do not change with respect to the variable, so their rate of change is zero.
What happens to the power of x in a term when you differentiate it?
-When differentiating a term, the power of x decreases by one. For example, if you have x^n, after differentiation it becomes n*x^(n-1).
What is the derivative of 1 over x squared?
-The derivative of 1 over x squared (1/x^2) is found by rewriting it as x to the power of -2 and then differentiating, which results in -2 times x to the power of -3.
How do you differentiate a sum of multiple terms?
-To differentiate a sum of multiple terms, you differentiate each term separately and then add the results together.
What is the derivative of x cubed?
-The derivative of x cubed (x^3) is found by applying the power rule, resulting in 3 times x squared (3x^2).
Why is it beneficial to rewrite fractions in a 'calculus-friendly' way?
-Rewriting fractions in a 'calculus-friendly' way, such as having the variable with the exponent on the top instead of the bottom, simplifies the differentiation process and makes it easier to apply the power rule.
Can you give an example of a physics-related derivative from the script?
-An example of a physics-related derivative in the script is the displacement versus time equation, where the derivative of displacement with respect to time (ds/dt) gives the velocity.
Outlines
📚 Introduction to Calculus Derivatives
This paragraph serves as an introduction to derivatives, focusing on polynomial functions. The speaker emphasizes the importance of understanding derivatives before progressing in calculus. By using a relatable analogy with Amazon Prime, the speaker explains the notation for derivatives and sets up the basic rule for differentiating powers of x. The main formula introduced is f'(x) = n * x^(n-1), where n is the exponent in the original function. The speaker underscores the significance of this rule by suggesting it will be frequently used, hence easily memorized, and prepares to offer numerous examples to solidify the understanding.
🧮 Advanced Derivative Calculations
In this paragraph, the complexity of derivatives increases as the speaker introduces scenarios involving higher exponents and negative exponents. Techniques for handling terms like 1/x and 1/x^2, which are rewritten as x^-1 and x^-2 to make them 'calculus-friendly', are detailed. The differentiation process is explained step-by-step, reinforcing the method of bringing the exponent to the front and reducing it by one. The speaker also explains how to manage constants in front of variables and their impact on the differentiation process, ultimately leading to an understanding of how to manipulate and simplify derivative expressions for practical use.
🔍 Simplifying Complex Derivatives
Here, the speaker deals with more complex functions involving sums and constants. The concept that the derivative of a constant is zero is highlighted as a critical takeaway. Through examples, the speaker illustrates the process of differentiating functions with mixed terms, including those with constants and variables, demonstrating the application of the power rule across different terms independently. This explanation aims to show how to systematically break down and differentiate a complex expression, preparing the learner to handle any polynomial derivative.
📉 Applying Derivatives in Physics
The final paragraph applies calculus to physics, specifically through the concept of displacement and time, translating these into velocity using derivatives. The speaker explains the differentiation of polynomial expressions in a physics context, using real-world units and constants. This practical application is tied to the fundamental physics formula for velocity, illustrating how derivatives directly apply to calculating changes in motion. The emphasis is on understanding how calculus tools can be used to solve physical problems, reinforcing the real-world relevance of calculus in scientific fields.
Mindmap
Keywords
💡Derivative
💡Polynomial
💡Exponent
💡Slope
💡Tangent Line
💡Prime Notation
💡Constant
💡Negative Exponents
💡Power Rule
💡Sum of Terms
💡Displacement and Velocity
Highlights
Derivatives are a fundamental concept in calculus, representing the rate of change of a function at a certain point.
Derivatives can be represented as 'y prime' or 'f prime of x', indicating the rate of change of y with respect to x.
The key to understanding derivatives is to visualize the gradient of a tangent line at a point without needing two points or drawing the line.
The power rule for derivatives states that the derivative of x to the power of n is n times x to the power of n minus 1.
A pro tip for remembering the power rule is to bring the exponent to the front and subtract 1 from the exponent.
When dealing with terms with a number in front, such as 4x^3, the number is multiplied by the exponent and the exponent is reduced by 1.
Negative exponents are handled by rewriting them as positive exponents with the base x on the bottom, such as 1/x^2 becoming x^(-2).
The derivative of a sum of terms is found by taking the derivative of each term separately and then adding the results.
Constants within a derivative equation are treated as factors that can often be factored out and simplified.
The derivative of a constant is always zero, as constants do not change with respect to the variable.
When rewriting expressions to be more 'calculus friendly', aim to have x terms with exponents rather than in the denominator.
The concept of 'cancelling out' derivatives, as humorously demonstrated, is not a valid mathematical process but can lead to correct results by coincidence.
The derivative of 1/x, which is a common example, results in -1/x^2, showcasing the power rule and handling of negative exponents.
The process of finding derivatives can be applied to physics problems, such as calculating velocity from displacement over time.
The equation of motion in physics can be derived mathematically using the principles of derivatives, relating initial speed, acceleration, and time.
Understanding the behavior of derivatives at various types of functions, including polynomials, is crucial for more advanced calculus and applications in fields like physics.
Transcripts
Browse More Related Video

01 - Basic Derivatives in Calculus, Part 1 - Learn what a Derivative is and how to Solve Them.
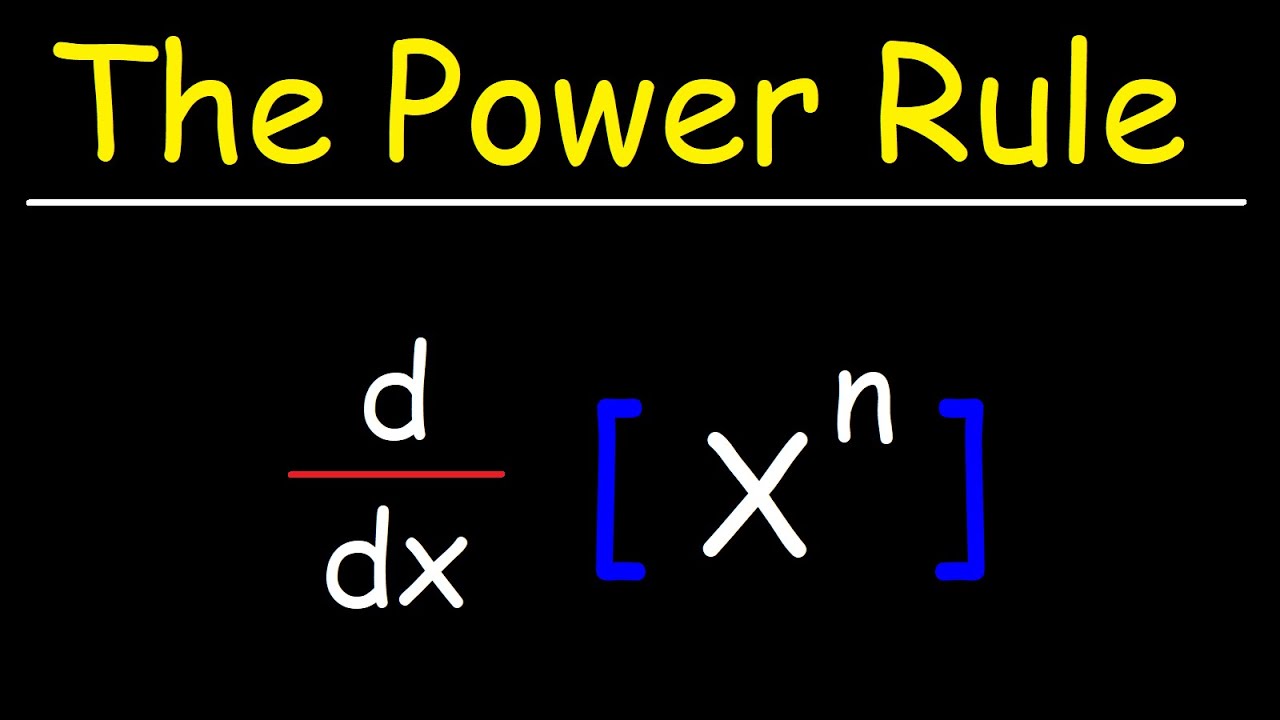
The Power Rule For Derivatives

Math 1325 Lecture 9 4 - Derivative Formulas

Basic Derivative Rules - Part 2: Combining the Rules

Techniques for Finding Derivatives

Calculus - How to find the derivative of a function using the power rule
5.0 / 5 (0 votes)
Thanks for rating: