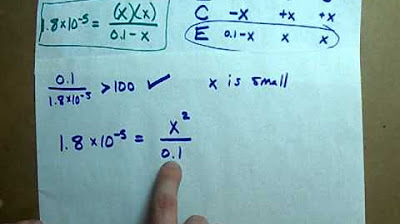Using Ka to calculate pH

JAMIE CAMP
4 Mar 201507:33
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of calculating pH using the acid dissociation constant (Ka), with a focus on acetic acid as an example. It outlines the dissociation equation, the initial concentration of acetic acid, and the assumption that the degree of ionization is small (less than 5%). The script details the steps to solve for the hydrogen ion concentration using the Ka expression and the assumption, then calculates the pH using the negative logarithm of the hydrogen ion concentration. The method is applicable when the ionization percentage is less than 5%, which is confirmed through a check calculation.

Takeaways
  • 📚 The discussion is about calculating pH using the Ka value, specifically for acetic acid with a Ka of 1.5 or 1.8 x 10^-5.
  • 🧪 The problem involves a 0.30 Molar solution of acetic acid and requires understanding its dissociation into hydrogen ions and acetate ions.
  • 📊 An ICE (Initial, Change, Equilibrium) table is used to set up the reaction, with initial concentration of acetic acid being 0.3 and changes denoted by 'X'.
  • 🔄 The reaction is assumed to proceed to the left, meaning the concentration of acetic acid decreases while those of hydrogen and acetate ions increase.
  • 📐 The Ka expression is used to relate the concentrations: Ka = [H+][CH3COO-] / [CH3COOH].
  • 🤔 The problem does not provide the pH, so the equilibrium concentrations must be determined to find the hydrogen ion concentration.
  • 📈 An assumption is made that the ionization percentage is small (<5%), simplifying the calculation by considering [H+] ≈ initial concentration of acid.
  • 🔢 The quadratic formula or equation solver would typically be used to find 'X' if the ionization percentage were significant, but it's not necessary in this case.
  • 🎯 The calculated hydrogen ion concentration [H+] is 2.3 x 10^-3 Molar, leading to a pH of 2.6 for the solution.
  • 🚨 The simplification method used is valid only when the ionization is less than 5%, which is confirmed by calculating an ionization percentage of 0.77%.
  • 📝 The process demonstrated is a practical approach to solving acid dissociation problems when certain assumptions about ionization can be made.
Q & A

  • What is the topic of discussion in the transcript?

    -The topic of discussion is how to use the Ka (acid dissociation constant) to calculate the pH of a solution, specifically using acetic acid as an example.

  • What is the Ka value for acetic acid mentioned in the transcript?

    -The Ka value for acetic acid mentioned is 1.5 or 1.8 times 10 to the negative fifth.

  • What is the molarity of the acetic acid solution discussed in the transcript?

    -The molarity of the acetic acid solution discussed is 0.30 M.

  • What is the dissociation equation for acetic acid?

    -The dissociation equation for acetic acid is CH3COOH (acetic acid) → H+ (hydrogen ion) + CH3COO- (acetate ion).

  • What is the initial concentration represented in the ICE table for the acetic acid solution?

    -The initial concentration represented in the ICE table is 0.3 M for acetic acid and 0 M for both hydrogen ions and acetate ions.

  • How does the assumption of a small percentage of ionization simplify the calculation?

    -The assumption of a small percentage of ionization (less than 5%) simplifies the calculation by allowing us to treat the change in concentration (X) as negligible, thus not requiring the use of the quadratic formula or a calculator to solve for X.

  • What is the calculated hydrogen ion concentration (X) in the example?

    -The calculated hydrogen ion concentration (X) in the example is 2.3 times 10 to the negative third M.

  • How is the pH of the solution calculated?

    -The pH of the solution is calculated using the formula pH = -log[H+], where [H+] is the hydrogen ion concentration. In this case, pH = -log(2.3 × 10^-3), which results in a pH of 2.6.

  • What is the percentage ionization for the acetic acid solution?

    -The percentage ionization for the acetic acid solution is 0.77%, which is calculated by dividing the hydrogen ion concentration at equilibrium (2.3 × 10^-3) by the initial acid concentration (0.30) and multiplying by 100.

  • Why is it important to check the percentage ionization?

    -It is important to check the percentage ionization to ensure it is less than 5%, which validates the assumption that the change in concentration (X) is negligible. If the percentage ionization were greater than 5%, the quadratic formula or a calculator would be necessary to solve for X accurately.

  • What is the significance of the quadratic formula in solving this problem?

    -The quadratic formula is significant in solving this problem when the percentage ionization is greater than 5% because it allows for the accurate calculation of the hydrogen ion concentration (X) from the Ka expression. However, in this example, the assumption of a small percentage ionization simplifies the process, making the quadratic formula unnecessary.

Outlines
00:00
📚 Calculating pH using KA: Introduction and Assumptions

This paragraph introduces the concept of calculating pH using the acid dissociation constant (KA) with a focus on acetic acid. It outlines the initial steps of the process, including the decomposition equation of acetic acid into hydrogen ions and acetate ions. The speaker emphasizes the typical approach of converting pH to hydrogen ion concentration but notes that this information is not provided in the current example. Instead, the speaker uses the given KA value and the initial concentration of acetic acid to set up an ICE (Initial, Change, Equilibrium) table. The key assumption made is that the ionization percentage is small enough to neglect the change in the initial concentration of the acid, simplifying the calculation process.

05:01
🧪 Solving the Problem with the Quadratic Formula and the 5% Rule

In this paragraph, the speaker discusses the algebraic approach to solving the problem without the pH value. The speaker explains how to use the KA expression and the ICE table to set up an equation, which typically requires solving using the quadratic formula or an equation solver. However, an assumption is made that the degree of ionization is less than 5%, which simplifies the calculation. The speaker demonstrates how to apply this assumption to approximate the hydrogen ion concentration and subsequently calculate the pH using the negative logarithm. The speaker also emphasizes the importance of verifying that the assumption holds by calculating the percentage of ionization and ensuring it is less than 5%. The explanation concludes with the solution's pH value and a reminder that this method is applicable when the ionization is below 5%, and otherwise, more complex mathematical methods would be necessary.

Mindmap
Keywords
💡Ka
Ka, or the acid dissociation constant, is a measure of the strength of an acid in a solution. It represents the equilibrium constant for the dissociation of the acid into its conjugate base and a hydrogen ion. In the video, the Ka of acetic acid is given as 1.8 times 10 to the negative fifth, which is used to calculate the pH of a 0.30 M solution. This value is crucial in understanding how the acetic acid dissociates in water and helps determine the hydrogen ion concentration, which is directly related to the pH of the solution.
💡pH
pH is a numerical scale used to specify the acidity or basicity of a solution. It is the negative logarithm (base 10) of the activity of hydrogen ions (H+) in a solution. The pH scale ranges from 0 to 14, with lower pH values indicating higher acidity and higher pH values indicating higher basicity. In the video, the goal is to calculate the pH of a 0.30 M acetic acid solution using the Ka value and the principles of chemical equilibrium.
💡Acetic Acid
Acetic acid is an organic compound with the chemical formula CH3COOH. It is a colorless liquid with a distinctive pungent smell and is the main component of vinegar. In the context of the video, acetic acid is used as an example to demonstrate how to calculate pH using its Ka value. Acetic acid is a weak acid, meaning it does not completely dissociate in water, which is why the calculation involves understanding the equilibrium between the undissociated acid and its ions.
💡Dissociation
Dissociation is the process in which a compound splits into two or more smaller molecules or ions when dissolved in a solvent. In the context of the video, the dissociation of acetic acid in water is described, where it forms a hydrogen ion (H+) and an acetate ion (CH3COO-). This process is central to understanding how the pH of a solution is determined, as the concentration of hydrogen ions is directly related to the pH value.
💡Equilibrium
Equilibrium in chemistry refers to the state in which the rates of the forward and reverse reactions are equal, and the concentrations of the reactants and products remain constant over time. In the context of the video, the equilibrium between the dissociated and undissociated forms of acetic acid is used to determine the hydrogen ion concentration, which is necessary for calculating the pH of the solution.
💡Hydrogen Ion Concentration
The concentration of hydrogen ions (H+) in a solution is a key factor in determining the pH. The higher the concentration of hydrogen ions, the lower the pH, indicating a more acidic solution. In the video, the calculation of the hydrogen ion concentration from the dissociation of acetic acid is essential to finding the pH of the solution.
💡Quadratic Formula
The quadratic formula is a mathematical formula used to solve quadratic equations, which are equations of the second degree with one variable. In the context of the video, the quadratic formula is mentioned as a method to solve for the unknown variable (X) representing the hydrogen ion concentration in the equilibrium expression, if the percentage of ionization is not small enough to make certain assumptions.
💡Percentage Ionization
Percentage ionization refers to the proportion of a compound that dissociates into ions in a solution. It is calculated by taking the concentration of the ions produced divided by the initial concentration of the compound, and then multiplying by 100. In the video, the percentage ionization is used to determine whether the assumption of a small ionization (less than 5%) is valid, which simplifies the calculation of the pH.
💡Logarithm
A logarithm is the exponent to which a number (the base) must be raised to obtain a given value (the true number). In the context of pH, the logarithm is used to convert the hydrogen ion concentration into a pH value, as pH is the negative logarithm of the hydrogen ion concentration. This transformation allows for a convenient scale to express the acidity or basicity of a solution.
💡Conjugate Base
In chemistry, a conjugate base is a species that results from the loss of a hydrogen ion (H+) from an acid. It is the anion that remains after the acid has donated a proton. In the video, the acetate ion (CH3COO-) is the conjugate base of acetic acid, formed when acetic acid donates a proton to water.
💡ICE Table
An ICE table, which stands for Initial, Change, Equilibrium table, is a method used in chemistry to organize and solve equilibrium problems. It outlines the initial concentrations of reactants and products, the changes that occur as the reaction reaches equilibrium, and the equilibrium concentrations after the reaction has taken place. In the video, the ICE table is used to visualize the changes in concentrations of acetic acid, hydrogen ions, and acetate ions as the system moves towards equilibrium.
Highlights

Introduction to calculating pH using Ka

Example problem with acetic acid and its Ka value

Decomposition equation for acetic acid

Initial concentration and ICE table setup

Assumption for small percentage of ionization

Simplification of the Ka expression

Algebraic approach without quadratic formula

Calculation of hydrogen ion concentration

Determination of pH using logarithm

Verification of the ionization percentage

Practical application of the 5% rule

Conclusion on solving the problem

Explanation of the 5% rule's applicability

Alternative methods for solving with higher ionization percentages

Relevance of the quadratic formula and graphing calculator in exams

Transcripts

Browse More Related Video

pH of a Weak Acid (0.1 M Acetic Acid) EXAMPLE

Calculate the pH of 0.1 M Acetic Acid

Calculating the pH of Weak Acids

Calculate Ka from pH ICE Table

Acid Dissociation Constant, Ka and pKa (A-Level Chemistry)

Calculate the Percent Ionization of 0.65 M HNO2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chemistry TutorialpH CalculationKa ValueAcetic AcidChemical EquilibriumAssumptions in ChemistryQuadratic FormulaIonization PercentageScientific MethodChemistry Education