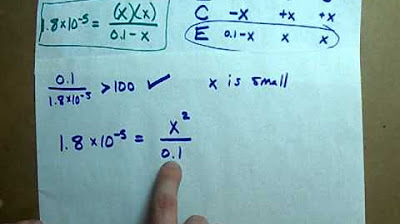Calculate the Percent Ionization of 0.65 M HNO2
TLDRThe video script explains the concept of percent ionization for a weak acid, using nitrous acid (HNO2) as an example. It details the process of calculating ionization by setting up an ICE (Initial, Change, Equilibrium) table and using the equilibrium constant (Ka). The script demonstrates a shortcut for solving the problem when the concentration of the acid is much larger than the Ka value, leading to the calculation that approximately 3.3% of the HNO2 at a concentration of 0.65 moles per liter will ionize in water.
Takeaways
- 🧪 The script discusses the calculation of percent ionization for a weak acid.
- 📈 The ionization process involves the weak acid molecules breaking apart in water to form H+ and NO2- ions.
- 🔍 The percent ionization is determined by the fraction of the original acid that dissociates upon dissolution in water.
- 🌟 The key value in this calculation is the acid dissociation constant (Ka) for the weak acid, which is given as 7.2 x 10^-4 for HNO2.
- 📊 The initial concentration of HNO2 is given as 0.65 moles per liter, with no initial H+ and NO2- present.
- 🎯 The equilibrium concentrations are calculated based on the initial concentration and the amount of HNO2 that ionizes.
- 📚 An ICE (Initial, Change, Equilibrium) table is used to set up the concentrations, but a shortcut is provided for cases where the Ka is very small.
- 🔢 The shortcut involves canceling out the -x term when the concentration of the acid is much larger than Ka, simplifying the equilibrium expression.
- 📈 The equilibrium expression is Keq = (concentration of H+ * concentration of NO2-) / concentration of HNO2.
- 🧠 The solution to the problem involves solving a quadratic equation, but the shortcut simplifies the process for small Ka values.
- 📱 The final result is the percent ionization, which is calculated as the ionized fraction (x) divided by the original concentration (0.65 moles per liter), yielding 3.3% for this example.
- 📝 The answer is rounded to two significant figures, and the focus is on the percent ionization rather than pH or other properties.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the calculation of the percent ionization for a weak acid in a given concentration.
What is a weak acid with a Ka value?
-A weak acid with a Ka value is an acid that partially ionizes in water, resulting in a relatively low concentration of H+ ions and its corresponding anion. The Ka value represents the acid dissociation constant, which is a measure of the strength of the acid in terms of its tendency to donate protons (H+) in solution.
What does percent ionization refer to?
-Percent ionization refers to the fraction of the weak acid molecules that dissociate into H+ ions and its corresponding anions when dissolved in water.
What is the significance of the equilibrium concentrations in the context of the script?
-The equilibrium concentrations are important because they represent the amounts of the reactants and products at the point of balance in the reaction. In the context of the script, these concentrations are used to set up an ICE (Initial, Change, Equilibrium) table, which helps in calculating the percent ionization without having to solve a quadratic equation.
What is the shortcut mentioned in the transcript for calculating percent ionization?
-The shortcut mentioned in the transcript is to avoid solving the equilibrium expression as a quadratic equation when the concentration of the weak acid is much larger than the Ka value. In such cases, the minus x terms can be canceled out, simplifying the calculation.
How is the equilibrium constant (Keq) expressed in the context of the weak acid ionization?
-The equilibrium constant (Keq) for the ionization of a weak acid is expressed as the product of the concentrations of H+ ions and the anions (NO2-) divided by the concentration of the undissociated weak acid (HNO2).
What was the initial concentration of HNO2 given in the example?
-The initial concentration of HNO2 given in the example was 0.65 moles per liter.
What was the Ka value used in the example?
-The Ka value used in the example was 7.2 times 10 to the negative 4th power.
What was the calculated percent ionization for the 0.65 M HNO2 solution?
-The calculated percent ionization for the 0.65 M HNO2 solution was approximately 3.3%.
How does the percent ionization relate to the original concentration of HNO2?
-The percent ionization represents the proportion of the original concentration of HNO2 that has dissociated into H+ and NO2- ions. In this case, out of the original 0.65 moles per liter, about 3.3% ionized, which corresponds to 0.0216 moles per liter.
What is the significance of the percent ionization value in understanding the behavior of weak acids in solution?
-The percent ionization value is significant as it provides insight into the degree to which a weak acid dissociates in solution. This information is crucial for understanding the acid's reactivity, its contribution to the pH of the solution, and its potential reactions with other substances.
Outlines
📚 Calculation of Percent Ionization for Weak Acids
This paragraph discusses the process of calculating the percent ionization of a weak acid with a given Ka value. It explains that percent ionization refers to the fraction of acid molecules that dissociate in water to form H+ and An- ions. The paragraph introduces the concept of an ICE (Initial, Change, Equilibrium) table to determine the initial, change, and equilibrium concentrations of the species involved. It emphasizes the significance of the equilibrium expression, Keq = [H+][An-]/[HA], and demonstrates how to solve for the equilibrium concentrations using a shortcut when the concentration of the acid is much larger than the Ka value. The example provided involves calculating the percent ionization of 0.65 M HNO2, resulting in approximately 3.3% ionization. The paragraph concludes by highlighting that the focus is on the fraction of the original concentration that ionizes, not on the pH or other properties.
Mindmap
Keywords
💡Percent Ionization
💡Weak Acid
💡Ka (acid dissociation constant)
💡Equilibrium
💡Equilibrium Expression
💡Conjugate Base
💡Ionization
💡Moles per Liter
💡Quadratic Equation
💡Shortcut Method
💡Significant Figures
Highlights
Calculating the percent ionization for a weak acid is discussed.
The weak acid in question has a given Ka value.
Percent ionization refers to the fraction of molecules that ionize in water.
An ICE (Initial, Change, Equilibrium) table is set up for the calculation.
A shortcut is provided for cases where the concentration is much larger than Ka.
The equilibrium concentrations are expressed as 0.65 - x, x, and x for H+, NO2-, and the undissociated acid respectively.
The equilibrium expression Keq is derived as the ratio of products to reactants.
The concentration of H+ and NO2- at equilibrium is x, and the concentration of HNO2 is 0.65 - x.
A method to avoid solving a quadratic equation is presented for small Ka values.
The minus x term can be ignored in the denominator if the concentration is much larger than Ka.
The calculation involves dividing the Ka value by the initial concentration and solving for x.
The value of x represents the amount of the original weak acid that dissociated.
The percent ionization is calculated by dividing x by the original concentration and expressing it as a percentage.
In this example, 0.0216 of the original 0.65 moles per liter dissociated.
The percent ionization is rounded to two significant figures for accuracy.
The final answer for percent ionization is 3.3% for an HNO2 concentration of 0.65 moles per liter.
The example demonstrates the process of calculating ionization without needing to find the pH.
This method is useful for understanding the behavior of weak acids in solution.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: