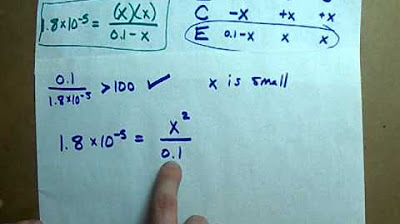Calculate the pH of 0.1 M Acetic Acid
TLDRThe video script explains the process of calculating the pH of a weak acid, specifically acetic acid, using the acid dissociation constant (Ka). It introduces the concept of an ICE table to determine the equilibrium concentrations and presents a shortcut method applicable when the initial concentration of the acid is much greater than Ka. The script then demonstrates how to solve for the hydrogen ion concentration and finally, how to calculate the pH using the negative logarithm of this concentration. The explanation is clear, engaging, and provides a step-by-step guide for students learning about weak acids and pH calculations.
Takeaways
- 📚 The calculation is for the pH of 1 mole per liter acetic acid, a weak acid with a given acid dissociation constant (Ka) of 1.8 x 10^-5.
- 🔄 Acetic acid partially dissociates in water to form H3O+ (or H+), acetate ions, and undissociated acetic acid, creating an equilibrium represented by an equilibrium arrow.
- 📈 The initial concentration of acetic acid is 0.1 moles per liter, and the equilibrium concentrations involve an unknown variable X, which represents the amount of dissociated acid.
- 🧪 The Ka expression is the product of the concentrations of the ions (H3O+ and acetate) divided by the concentration of the undissociated acid, with water's concentration ignored as it is in excess.
- 🔢 The Ka value can be rearranged to solve for the H+ concentration (X) using quadratic expressions or by taking the square root of Ka times the initial concentration if certain conditions are met.
- 🎯 When the initial concentration is significantly higher than the Ka, a shortcut is applicable where the term (concentration - X) can be approximated as the original concentration for simplification.
- 📊 The pH is calculated by taking the negative logarithm (log) of the H+ concentration, which in this case is the square root of the product of Ka and the initial concentration.
- 🤓 The use of the quadratic formula is necessary when the assumption for simplification does not hold, requiring solving for X before calculating the pH.
- 🌟 The script emphasizes the beauty of the process, highlighting that understanding the setup of Ka = X^2 / (C - X) allows for straightforward pH calculations for weak acids.
- 📝 It is suggested to maintain two decimal places for pH values for clarity and consistency, although some educators may prefer different rounding rules.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the process of calculating the pH of a weak acid, specifically acetic acid, using the acid dissociation constant (Ka).
What is the acid dissociation constant (Ka) for acetic acid mentioned in the transcript?
-The acid dissociation constant (Ka) for acetic acid mentioned in the transcript is 1.8 times 10 to the negative 5.
What does it mean for an acid to be weak?
-A weak acid is one that does not completely dissociate in water, meaning it does not yield a 100% concentration of H3O+ or H+ ions when mixed with water.
What is the initial concentration of acetic acid given in the example?
-The initial concentration of acetic acid given in the example is 0.1 moles per liter.
What is the significance of the equilibrium concentrations in the pH calculation?
-The equilibrium concentrations are important in the pH calculation because they represent the concentrations of the ions and molecules at equilibrium, which are used to calculate the Ka and ultimately the pH of the solution.
What is the formula for calculating Ka in the context of the given problem?
-The formula for calculating Ka in the context of the given problem is Ka = [H3O+][A-] / [HA], where [H3O+] and [A-] are the equilibrium concentrations of the acetate ion and hydronium ion, respectively, and [HA] is the equilibrium concentration of the acetic acid.
What is the shortcut method for solving the quadratic expression in the pH calculation?
-The shortcut method for solving the quadratic expression is to assume that if the initial concentration (C) divided by Ka is greater than a certain threshold (like 100, 500, or 1000), then the term -X in the denominator can be ignored because X is very small compared to C.
What is the relationship between the H+ concentration and the initial concentration and Ka in the pH calculation?
-The H+ concentration in the pH calculation can be estimated as the square root of Ka times the initial concentration (C), assuming that C is high enough relative to Ka.
How is the pH calculated from the H+ concentration?
-The pH is calculated from the H+ concentration by taking the negative logarithm (log) of the H+ concentration.
What is the final calculated pH of the acetic acid solution in the example?
-The final calculated pH of the acetic acid solution in the example is approximately 2.87 or 2.9, depending on the number of significant figures used.
What are the two main methods for calculating the pH of a weak acid?
-The two main methods for calculating the pH of a weak acid are using an ICE table (Initial, Change, Equilibrium) to solve the problem in full or using a shortcut formula that takes advantage of the assumption that X is very small compared to the initial concentration.
Outlines
📚 Calculating pH of Acetic Acid
This paragraph discusses the process of calculating the pH of a 1 mole per liter acetic acid solution, a weak acid. The key constant required for this calculation is the acid dissociation constant (Ka), which is given as 1.8 times 10 to the negative 5. The explanation highlights that a weak acid does not fully dissociate in water, resulting in an equilibrium between the acid and its ions. The concept of H3O+ (hydrated hydrogen ion) is introduced, and the equilibrium reaction is described with its respective concentrations in the form of an ICE table (Initial, Change, Equilibrium). The paragraph then delves into the method of solving for the hydrogen ion concentration using either the full ICE table or a shortcut based on the Ka and initial concentration of the acid. The quadratic formula is briefly mentioned as a tool for solving the equilibrium expression, but the focus is on the shortcut method, which simplifies the calculation when the initial concentration is much greater than Ka.
📈 Simplifying pH Calculation with Assumptions
The second paragraph continues the discussion on calculating the pH of acetic acid by focusing on the simplification of the process using assumptions. It explains that if the initial concentration of the acid divided by the Ka is significantly greater than 1, the minus X term in the equilibrium expression can be neglected because X is very small compared to the initial concentration. This leads to a simplified calculation of the hydrogen ion concentration as the square root of Ka times the initial concentration. The paragraph then demonstrates how to use this concentration to calculate the pH, which is the negative logarithm of the hydrogen ion concentration. The process is illustrated with calculations, leading to a pH value of approximately 2.87, which is then rounded to two decimal places for clarity. The paragraph concludes by emphasizing the beauty of the method, which allows for the straightforward determination of the pH of weak acids given the Ka value.
Mindmap
Keywords
💡pH
💡acetic acid
💡Ka
💡weak acid
💡equilibrium
💡H3O+
💡concentration
💡ICE table
💡quadratic formula
💡log
💡shortcut
Highlights
Calculating the pH of 0.1 mole per liter acetic acid solution.
Acetic acid is a weak acid with a Ka of 1.8 x 10^-5.
Weak acids do not dissociate completely in water, resulting in an equilibrium between H3O+, acetate ions, and the undissociated acid.
The concept of H3O+ is introduced, representing water with an extra H.
An equilibrium arrow is used to represent the reversible reaction of acetic acid dissociation in water.
The initial and equilibrium concentrations of acetic acid, H3O+, and acetate ions are represented with a variable X.
The relationship between Ka, the concentrations of H3O+ and acetate ions, and the initial concentration of acetic acid is expressed as an equation.
A shortcut formula for calculating the H+ concentration in weak acid solutions is discussed, relating it to the square root of Ka times the initial concentration.
The condition for using the shortcut formula is when the initial concentration divided by Ka is greater than certain thresholds (e.g., 100, 500, or 1000).
A practical example is given where the initial concentration of acetic acid is high enough to use the shortcut formula.
The H+ concentration (X) is calculated using the square root of Ka times the initial concentration.
The pH is determined by taking the negative logarithm (log) of the H+ concentration.
The final pH of the acetic acid solution is calculated to be approximately 2.87, with a discussion on significant figures.
The process of calculating the pH of a weak acid like acetic acid is summarized, emphasizing the use of Ka and the conditions for using the shortcut formula.
The importance of understanding the dissociation of weak acids in water and the calculation of pH is highlighted for practical applications.
The method for solving for the H+ concentration using the quadratic formula is mentioned as an alternative when the shortcut formula is not applicable.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: