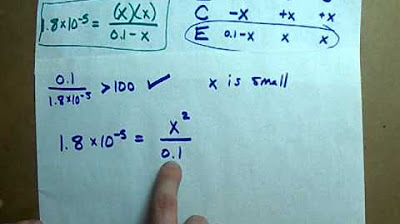Calculating the pH of Weak Acids

MaChemGuy
1 Apr 201504:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the process of calculating the pH of a weak acid using the acid dissociation constant (Ka). It explains that unlike strong acids, weak acids do not fully dissociate, necessitating a different approach for pH calculation. The script introduces the concept of partial dissociation and how it affects the hydrogen ion concentration, which is crucial for pH determination. It simplifies the calculation by equating the concentration of the weak acid at equilibrium with its initial concentration, highlighting that the degree of dissociation is minimal. The script provides a step-by-step guide on using the Ka value to find the H+ concentration and ultimately the pH, offering examples with specific Ka values for illustrative purposes.

Takeaways
  • 📚 The video discusses the method to calculate the pH of a weak acid using a four-week model.
  • 🔄 For weak acids, the acid dissociation constant (Ka) is used instead of direct concentration due to partial dissociation.
  • 📈 The H+ concentration is calculated using the formula: √(Ka * [HA]).
  • 🧪 The approximation made in the calculation assumes the original concentration of the weak acid to be equal to the concentration at equilibrium.
  • 🔢 The dissociation of the weak acid is minimal, justifying the approximation of using the initial concentration in calculations.
  • 🌟 The script provides an example calculation for a weak acid with a given Ka value, showing how to find the pH.
  • 📊 Two examples are given: one with a pH of 2.5 and another with a pH of 2.9, both calculated using the weak acid dissociation method.
  • 🥼 The concept of a monobasic acid is reviewed, which donates one proton upon dissociation.
  • 🧬 The difference between strong and weak acids is highlighted, with strong acids fully dissociating and weak acids only partially dissociating.
  • 🎯 The importance of understanding the dissociation process is emphasized for accurate pH calculation.
  • 📚 The video serves as an educational resource for understanding the pH calculation of weak acids.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to calculate the pH of a weak acid using the four-week model and the acid dissociation constant (Ka).

  • What is the difference between strong acids and weak acids in terms of dissociation?

    -Strong acids undergo complete dissociation, meaning the concentration of H+ ions is directly known from the acid concentration. Weak acids, however, have partial dissociation, and their H+ concentration cannot be directly determined from the acid concentration.

  • What is the acid dissociation constant (Ka)?

    -The acid dissociation constant (Ka) is a value that describes the extent to which a weak acid dissociates in water, and it is used to calculate the hydrogen ion concentration in the pH calculation of weak acids.

  • How is the H+ concentration calculated for a weak acid?

    -The H+ concentration for a weak acid is calculated using the square root of the product of the Ka and the initial concentration of the weak acid (Ha).

  • What is the approximation made in the calculation of pH for weak acids?

    -The approximation made is that the concentration of the weak acid (Ha) used in the calculation is considered to be the original concentration, even though in reality, it is the concentration at equilibrium. This approximation is acceptable because the degree of dissociation is usually very small.

  • What happens when a weak acid dissociates in water?

    -When a weak acid dissociates in water, it produces H+ ions and its corresponding conjugate base (A-). The amount of dissociation is typically very small, so the concentration of the acid at equilibrium is approximately equal to the original concentration.

  • How do you determine the pH of a weak acid solution?

    -To determine the pH of a weak acid solution, you first calculate the H+ concentration using the Ka value and the initial concentration of the weak acid. Then, you use the H+ concentration to calculate the pH by taking the negative logarithm (log) of the H+ concentration.

  • What is the pH of a 0.1 M solution of a weak acid with a Ka value of 1.8 x 10^-5?

    -To calculate the pH, first find the H+ concentration using the formula H+ = sqrt(Ka * [Ha]). Then, use the H+ concentration to calculate the pH by taking the negative log of the H+ concentration. In this case, the pH is found to be 2.5.

  • What is the relationship between the concentration of the weak acid (Ha) and its dissociated H+ and A- ions at equilibrium?

    -At equilibrium, the concentration of the weak acid (Ha) is reduced by the amount of dissociation (X), while the concentrations of H+ and A- ions are both equal to X. The ratio of these concentrations remains 1:1 throughout the dissociation process.

  • Why is the original concentration of the weak acid used in the pH calculation?

    -The original concentration of the weak acid is used in the pH calculation because the degree of dissociation is very small, making it safe to approximate that the concentration at equilibrium is the same as the original concentration. This simplifies the calculation and provides an acceptable approximation for the H+ concentration.

  • What is the pH of a 0.1 M solution of ethanoic acid with a Ka value of 1.7 x 10^-5?

    -Following the same process as for the previous weak acid, the pH of the ethanoic acid solution is calculated to be 2.9.

Outlines
00:00
📚 Understanding pH Calculation for Weak Acids

This paragraph introduces the concept of calculating the pH of a four-week model using basic assets. It explains the difference between strong and weak acids, highlighting that while strong acids fully dissociate, weak acids only partially dissociate. The importance of knowing the hydrogen ion concentration for pH calculation is emphasized. The paragraph then delves into the use of the acid dissociation constant (Ka) for calculating the pH of weak acids, presenting the formula and explaining the approximation involved. The process of how weak acids dissociate and the rationale behind using the original concentration of the acid in equilibrium calculations are also discussed, with examples provided to illustrate the calculation of pH for acetic acid and ethanoic acid.

Mindmap
Keywords
💡pH calculation
The process of determining the acidity or basicity of a solution, quantified by the pH scale. In the video, the focus is on calculating the pH for weak acids, which involves understanding the dissociation of the acid and the concentration of hydrogen ions (H+). The script explains that for strong acids, this process is straightforward due to complete dissociation, but weak acids require a different approach using the acid dissociation constant (Ka).
💡monobasic acid
A type of acid that donates only one proton (H+) when it dissociates in water. The video emphasizes that the term 'monobasic' refers to the single proton donating ability of the acid, which is relevant when discussing the dissociation process and calculating the pH.
💡strong acids
Acids that completely dissociate in water, releasing all of their protons (H+) into the solution. The video contrasts strong acids with weak acids, noting that the complete dissociation of strong acids makes the calculation of pH simpler because the concentration of H+ directly corresponds to the concentration of the acid.
💡weak acids
Acids that partially dissociate in water, releasing only a fraction of their protons (H+). The video explains that weak acids require a different calculation method for pH due to this partial dissociation, which is not the case for strong acids. The dissociation of weak acids is described using the acid dissociation constant (Ka).
💡acid dissociation constant (Ka)
A constant that quantifies the extent to which an acid dissociates in water. In the context of the video, the Ka value is crucial for calculating the pH of weak acids, as it allows for the determination of the hydrogen ion (H+) concentration when complete dissociation does not occur.
💡partial dissociation
The process by which a weak acid only partially releases its protons (H+) into a solution. This is in contrast to strong acids, which fully dissociate. The video emphasizes that the degree of dissociation for weak acids is often small, which affects how the pH is calculated.
💡hydrogen ion concentration
The concentration of H+ ions in a solution, which is directly related to the acidity of the solution and is a key factor in determining the pH. The video script explains that knowing the hydrogen ion concentration is essential for calculating the pH of any solution, including both strong and weak acids.
💡equilibrium
A state in which the concentrations of reactants and products in a chemical reaction remain constant over time. In the context of the video, equilibrium refers to the point at which the weak acid has partially dissociated, and the concentrations of the acid and its ions (H+ and A-) are in a fixed ratio.
💡approximation
A simplified estimation or assumption made in calculations to make them more manageable. The video script mentions an approximation that is used when calculating the pH of weak acids, acknowledging that while it simplifies the process, it is still an acceptable method.
💡concentration of the acid
The amount of acid present in a given volume of solution, often expressed in moles per liter (M). In the video, the initial concentration of the acid is important for calculating the equilibrium concentrations and ultimately the pH.
💡logarithm
A mathematical operation that calculates the power to which a number (the base) must be raised to produce a given value. In the context of pH calculation, the logarithm is used to find the pH from the hydrogen ion concentration, as the pH scale is logarithmic.
Highlights

The video discusses the calculation of pH for weak acids using a four-week model.

The fundamental difference between strong and weak acids is that strong acids completely dissociate, while weak acids only partially dissociate.

The formula for a monobasic weak acid dissociation is explained, emphasizing the one-to-one ratio of concentrations.

The acid dissociation constant (Ka) is introduced as a key factor in calculating the pH of weak acids.

The H+ concentration for weak acids is determined using the square root of the Ka value multiplied by the concentration of the acid (Ha).

An approximation is made in the calculation where the original concentration of the acid is used in place of the equilibrium concentration.

The concept of dissociation is clarified, explaining that a small amount of the weak acid (Ha) dissociates into H+ and A- at equilibrium.

It is highlighted that the concentration of dissociation is minimal, justifying the use of the original concentration in calculations.

An example calculation is provided for a weak acid with a given Ka value, showing how to find the pH.

The importance of understanding the original concentration of the acid and its role in the pH calculation is emphasized.

The calculation process for pH is demonstrated with a specific example, yielding a pH value of 2.5.

Another example is given, this time with a different weak acid and Ka value, resulting in a pH of 2.9.

The video provides a clear methodology for calculating the pH of weak acids, which is crucial for understanding acid-base chemistry.

The role of the Ka value in the pH calculation for weak acids is underscored, showing its significance in the process.

The video offers a practical approach to understanding the behavior of weak acids in solution, which is essential for various scientific and industrial applications.

The concept of equilibrium in acid dissociation is explained, which is fundamental to the understanding of the pH calculation for weak acids.

The video concludes with a summary of the steps and considerations needed to calculate the pH of weak acids, reinforcing the key points discussed.

Transcripts

Browse More Related Video

Acid Dissociation Constant, Ka and pKa (A-Level Chemistry)

Calculate the pH of 0.1 M Acetic Acid

pH of a Weak Acid (0.1 M Acetic Acid) EXAMPLE

Ka - calculating the pH of a weak acid

Find the Ka of an acid (Given pH) (0.1 M Hypochlorous acid) EXAMPLE

Using Ka to calculate pH

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ChemistrypH CalculationWeak AcidsDissociation ConstantAcid-Base EquilibriumScientific TutorialEducational ContentChemical PropertiesMathematical ApproachAcademic Lecture