Integration By Parts - Tabular Method

The Organic Chemistry Tutor
22 Mar 201818:09
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a detailed explanation of the tabular method for integration by parts, demonstrating its application on various integral problems. It walks through the process of setting up the table with signs, derivatives, and integrals, and highlights when to use or avoid this method. The examples include integrating products of polynomials and exponentials, as well as trigonometric functions, providing a comprehensive understanding of the technique.

Takeaways
  • 📚 Integration by parts is a technique used to compute integrals by breaking them down into simpler components.
  • 📊 The tabular method is a quick way to apply integration by parts, involving the creation of a table with columns for signs, derivatives, and integrals.
  • 🔢 When using the tabular method, the first step is to identify u and dv, and then find their derivatives and integrals accordingly.
  • 🌟 The formula for integration by parts is ∫(uv')dx = uv - ∫(vdu), where u and v' are functions derived from u and dv, respectively.
  • 🔄 The signs in the tabular method alternate, starting with a positive sign for the first term and continuing in a positive-negative-positive-negative pattern.
  • 🧩 For the integral of x^2 * e^x dx, the tabular method results in x^2 * e^x - 2x * e^x + 2 * e^x + C.
  • 📈 When dealing with the integral of x^3 * sin(x) dx, the tabular method is also applicable, yielding -x^3 * cos(x) + 3x^2 * sin(x) + 6x * cos(x) - 6 * sin(x) + C.
  • 📝 For certain integrals, like ∫(x^5 * ln(x))dx, it's more efficient to use the standard integration by parts formula rather than the tabular method.
  • 🔧 The tabular method is not suitable when the derivatives or integrals of u and dv do not result in a zero value, as seen with ∫(x^5 * ln(x))dx.
  • 🌐 The tabular method can be applied to integrals like ∫(x^4 * sin(x))dx or ∫(x^7 * e^(4x))dx, where repetitive functions are involved.
Q & A

  • What is the tabular method for integration by parts?

    -The tabular method for integration by parts is a systematic way of applying the integration by parts formula. It involves creating a table with three columns: signs, derivatives, and integrals. The method helps to keep track of the alternating signs and the derivatives and integrals of the functions involved in the integration by parts process.

  • How is the integration by parts formula expressed?

    -The integration by parts formula is expressed as ∫(u dv) = u*v - ∫(v du). Here, 'u' and 'dv' are the two functions being integrated, and 'v' and 'du' are their respective integrals and derivatives.

  • What are the steps to apply the tabular method for the integral of x^2 * e^x dx?

    -First, create a table with columns for signs, derivatives, and integrals. Assign u = x^2 and dv = e^x dx. Find the derivatives and integrals for u and dv, respectively. Then, fill in the table following the alternating signs and calculate the result by multiplying the corresponding entries and combining the terms.

  • What is the result of the integral of x^2 * e^x dx using the tabular method?

    -The result is x^2 * e^x - 2x * e^x + 2 * e^x + C, where C is the constant of integration.

  • How does the tabular method help in solving the integral of x^3 * sin(x) dx?

    -The tabular method allows us to systematically apply integration by parts. For this integral, we assign u = x^3 and dv = sin(x) dx. We find the derivatives and integrals accordingly and fill in the table. The result is -x^3 * cos(x) + 3x^2 * sin(x) + 6x * cos(x) - 6 * sin(x) + C.

  • Why is the tabular method not recommended for the integral of x^5 * ln(x) dx?

    -The tabular method is not recommended for the integral of x^5 * ln(x) dx because the process involves repeated differentiation and integration by parts, and the tabular method does not lead to a simpler solution. It's more efficient to use the standard integration by parts formula directly.

  • What is the final result of the integral of x^5 * ln(x) dx?

    -The final result is (1/6)x^6 * ln(x) - (1/6)x^6 + C, where C is the constant of integration.

  • How can you determine if the tabular method is suitable for a given integral?

    -The tabular method is suitable when the derivatives and integrals of the functions involved do not lead to repetitive or non-convergent series. If the process results in repetitive functions or does not reach a zero in the derivatives or integrals columns, it's better to use the standard integration by parts formula.

  • What is the result of the integral of e^x * sin(x) dx?

    -The result is (1/2)e^x * sin(x) - (1/2)e^x * cos(x) + C, where C is the constant of integration.

  • How do repetitive functions in the tabular method affect the process?

    -Repetitive functions in the tabular method indicate that the derivatives and integrals do not simplify to reach a zero value. This makes the tabular method inefficient and leads to a non-terminating series, which is why it's better to use the standard integration by parts formula in such cases.

  • What are the key differences between the tabular method and the standard integration by parts formula?

    -The tabular method is a structured approach that uses a table to organize and simplify the integration by parts process, making it easier to handle complex integrals. The standard integration by parts formula is a direct application of the formula without the structured table approach, which may be simpler for some integrals but can become cumbersome for others.

  • What is the significance of the constant of integration 'C' in the results?

    -The constant of integration 'C' is included in the results to account for the arbitrary constant that arises when finding the antiderivative of a function. It represents the infinite number of possible antiderivatives that differ by a constant value.

Outlines
00:00
📚 Introduction to Integration by Parts using Tabular Method

This paragraph introduces the concept of integration by parts, specifically focusing on the tabular method. It explains the process of setting up a table with columns for signs, derivatives, and integrals. The example of integrating x^2 * e^x is used to demonstrate how to apply the formula for integration by parts, which is ∫(u dv) = u*v - ∫(v du). The paragraph walks through the steps of selecting u and dv, finding their derivatives and integrals, and filling out the table to arrive at the final answer. The explanation emphasizes the alternating signs and how to use the table to calculate each term of the integral.

05:02
📈 Solving Definite Integrals using Tabular Method

In this paragraph, the focus is on solving a specific problem: finding the indefinite integral of x^3 * sin(x) dx. The video script outlines the tabular method, starting with establishing the signs, derivatives for the u term, and integral for dv. It differentiates x^3 to find u', u'', and u''', and integrates sin(x) to find v and v'. The paragraph then combines these results to fill out the table and calculate the integral using the integration by parts formula. It also emphasizes the importance of checking the derivatives and integrals for accuracy and concludes with the final answer, including the constant of integration, c.

10:04
🚫 When Not to Use the Tabular Method for Integration by Parts

This paragraph discusses situations where the tabular method for integration by parts is not recommended. It uses the example of integrating x^5 * ln(x) dx to illustrate why the standard integration by parts formula should be used instead. The video explains that the tabular method is not suitable when the derivatives or integrals do not result in a zero, as seen with the derivatives of ln(x) and the integrals of x^5. The paragraph concludes with a recommendation to use the standard method for this type of problem and introduces another problem where the tabular method is not applicable.

15:05
🤔 Analyzing the Appropriate Use of Tabular Method for Specific Integrals

The final paragraph delves into the analysis of when to use the tabular method for integration by parts. It presents two scenarios: one where the tabular method is suitable (integral of x^4 * sin(x)) and another where it is not (integral of e^x * sin(x) dx). The paragraph explains the reasoning behind choosing the appropriate method based on the repetitiveness of the derivatives and integrals. It concludes with a worked-out example of the integral of e^x * sin(x) dx using the standard integration by parts formula, highlighting the process of simplifying and combining like terms to arrive at the final answer, which includes the constant of integration, c.

Mindmap
Keywords
💡Integration by Parts
Integration by Parts is a technique used in calculus to evaluate integrals when the function to be integrated is a product of two functions. The method is based on the product rule for derivatives and allows us to break down a complex integral into simpler ones. In the video, this method is used to solve integrals such as ∫x²e^x dx and ∫x³sin(x) dx, where the integral is expressed as a product of two functions, u and dv, and the formula ∫udv = uv - ∫vdu is applied.
💡Tabular Method
The Tabular Method is a systematic approach to performing integration by parts, where the process is organized into a table with columns for signs, derivatives, and integrals. This method helps to keep track of the alternating signs and the derivatives and integrals of the functions involved. It is particularly useful when dealing with multiple integration by parts applications in a single problem.
💡Derivative
A derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its independent variable. In the context of integration by parts, finding the derivative of the function u is crucial as it will become a part of the integral expression we are trying to evaluate.
💡Integral
An integral represents the accumulated area under a curve or the antiderivative of a function. In the process of integration by parts, finding the integral of dv is necessary to express the original integral in terms of simpler functions. Integrals are calculated for each term in the tabular method and contribute to the final answer.
💡Alternating Signs
Alternating signs refer to the pattern of positive and negative signs that occur in the integration by parts formula. The signs alternate between positive and negative as we progress through the terms of the integral expression, starting with a positive sign for the first term.
💡Antiderivivative
An antiderivative is a function whose derivative is the given function we are trying to integrate. In other words, finding the antiderivative of a function allows us to determine the integral. The process of finding an antiderivative is called integration.
💡Power Rule
The power rule is a fundamental rule in calculus that states that the derivative of a function of the form x^n, where n is any real number, is nx^(n-1). This rule is used extensively in differentiation and integration, especially when dealing with polynomial functions.
💡Constant of Integration
The constant of integration, often denoted by 'C', is an additional term that is included in the antiderivative of a function to account for the infinite number of points where the area under the curve could start. It represents the arbitrary constant that can be added to any antiderivative without changing the derivative.
💡Repetitive Functions
Repetitive functions are those that have the same derivative or integral form repeatedly. In the context of integration by parts, if the derivatives or integrals of the functions involved do not eventually reach zero or a simple form, the process can become complex and the tabular method may not be suitable.
💡Definite Integral
A definite integral represents the specific numerical value of the accumulated area under a curve between two points on the x-axis. It is denoted by the integral symbol with upper and lower limits. Definite integrals are often used to find the net area or to calculate quantities in physics and engineering.
💡Product Rule
The product rule is a fundamental rule in calculus that describes how to differentiate the product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. The product rule is the basis for the integration by parts formula.
Highlights

Introduction to the tabular method for integration by parts.

Using the tabular method to find the integral of x squared times e to the x.

The integration by parts formula: integral of u dv = u times v - integral of v du.

Constructing the table with signs, derivatives, and integrals for the tabular method.

Derivative and integral calculations for u = x squared and dv = e to the x.

Applying the tabular method to find the integral of x cubed times sine x.

Derivative and integral calculations for u = x cubed and dv = sine x.

Integration by parts for the function x to the fifth times ln x without using the tabular method.

Derivative and integral calculations for u = ln x and dv = x to the fifth dx.

Explanation of when not to use the tabular method for integration by parts.

Attempt to apply the tabular method to the integral of e to the x times sine x.

Derivative and integral calculations for u = sine x and dv = e to the x dx.

Using the integration by parts formula directly for e to the x times sine x integral.

Explanation of the repetitive nature of certain functions affecting the tabular method's applicability.

Final answer for the integral of e to the x times sine x using integration by parts.

Guidance on choosing between the tabular method and traditional integration by parts.

Examples of problems suitable for the tabular method.

Transcripts

Browse More Related Video

Indefinite Integral - Basic Integration Rules, Problems, Formulas, Trig Functions, Calculus

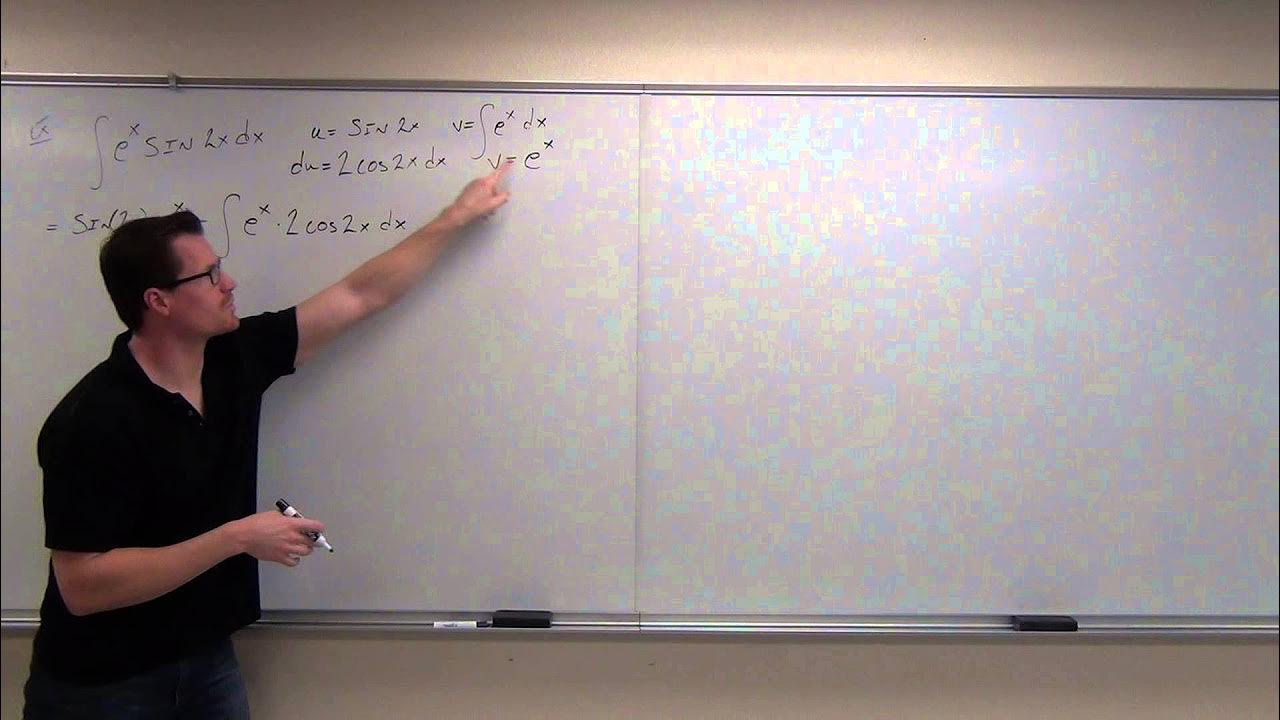
Calculus 2 Lecture 7.1: Integration By Parts

Math1325 Lecture 13 6

Integration By Parts

Integrating Exponential Functions By Substitution - Antiderivatives - Calculus

Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
IntegrationByPartsTabularMethodCalculusTipsMathematicsEducationDifferentialCalculusIntegralSolvingOnlineLearningMathTutorialsEducationalContentMathematicalAnalysis