Essential & Practical Circuit Analysis: Part 1- DC Circuits

The paragraph introduces the concept of circuit analysis as a fundamental toolkit for understanding and designing complex circuits. It emphasizes the importance of grasping the foundational concepts of circuit analysis before delving into electronics or electronic systems. The video aims to cover a range of topics starting from basic circuits to more complex ones, including linear circuit elements, Ohm's law, series and parallel circuits, voltage and current dividers, Kirchhoff's laws, and Thevenin and Norton equivalent circuits.

This section focuses on the basic components of a circuit such as nodes, branches, and loops, and how they function within a circuit. It explains Ohm's law, which is a fundamental relationship in circuit analysis, and how it can be used to calculate unknown values of voltage, current, or resistance in a circuit. The paragraph also discusses the difference between series and parallel connections of circuit elements and how to calculate equivalent resistance in these configurations.

The discussion moves on to voltage dividers, explaining how they work in a series circuit and how to calculate the output voltage using resistor values. It also covers the effect of attaching a load to a voltage divider and how it changes the output voltage. The concept of current dividers is briefly introduced, highlighting the difference between voltage and current dividers and their applications in real-world circuits.

This part introduces Kirchhoff's Current Law (KCL), which states that the sum of all currents entering a node must equal the sum of all currents exiting the node. The paragraph provides examples and illustrations to help understand KCL and its application in solving for unknown currents in a circuit. It also sets the stage for further exploration into nodal analysis, which uses KCL to determine node voltages.

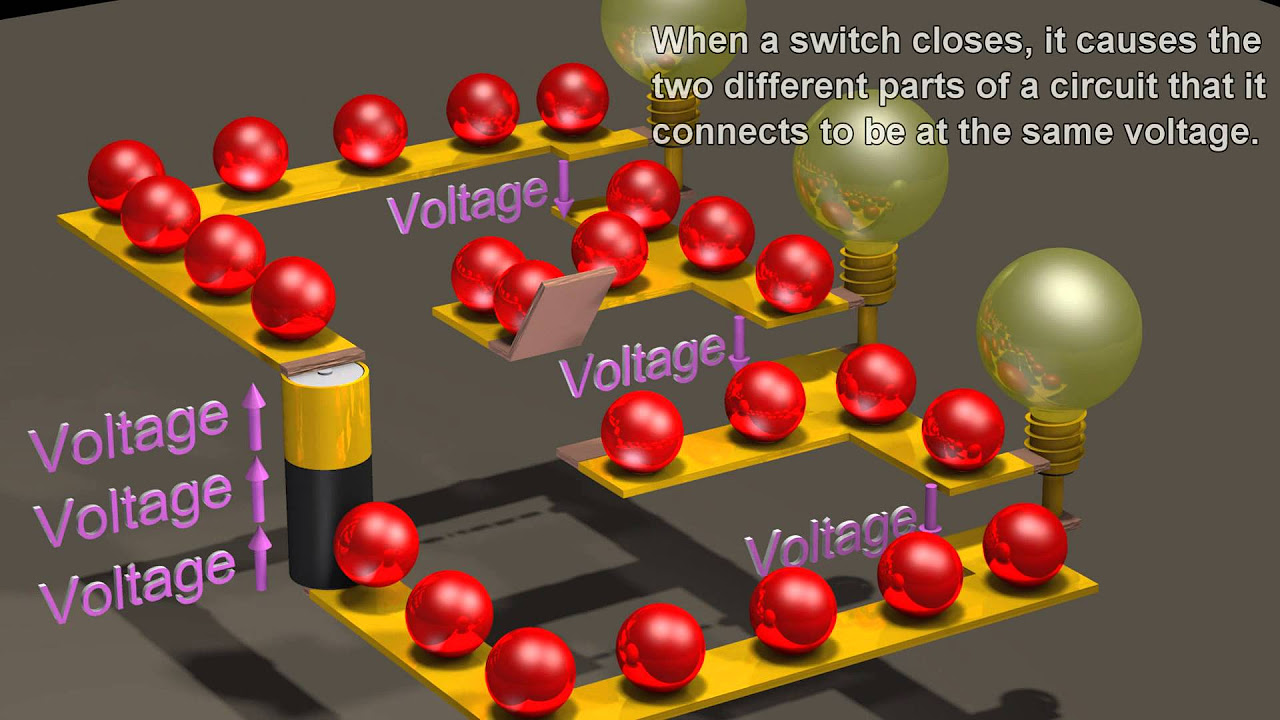
The paragraph delves into nodal analysis, a technique for solving for node voltages using KCL. It explains the process of setting up reference nodes and writing KCL equations for each node in the circuit. The discussion then transitions to Kirchhoff's Voltage Law (KVL), which states that the sum of all voltage drops in a closed loop must equal the sum of all voltage rises. The paragraph provides an analogy of skiing to illustrate KVL and demonstrates how to apply it to solve for unknown voltages in a circuit.

This section introduces Thevenin and Norton equivalent circuits, which are simplified representations of a complex circuit. It explains the process of source transformation, which allows the conversion between Thevenin and Norton circuits, and how to find the equivalent resistance and voltage or current for these representations. The paragraph emphasizes the usefulness of these equivalent circuits in simplifying circuit analysis and making it easier to understand the behavior of complex circuits.

The Superposition Theorem is introduced as a powerful tool for analyzing circuits with multiple sources. The theorem allows the consideration of one source at a time and the addition of their individual effects to find the total effect. The paragraph outlines the steps for applying the Superposition Theorem, including setting all but one source to zero, solving for the necessary currents and voltages, and summing the solutions to find the actual values. The theorem is demonstrated through an example that involves finding the voltage across a resistor using the theorem.

The conclusion of the video script emphasizes the importance of practice in mastering circuit analysis. It encourages viewers to experiment with real circuits and use simulation software like LT Spice to verify their findings and explore circuit behavior. The video creator shares personal insights on the challenges of identifying the appropriate technique for a given circuit and the value of hands-on experience. The script ends with a call to action for viewers to provide feedback and engage with the content by liking and subscribing to the channel.