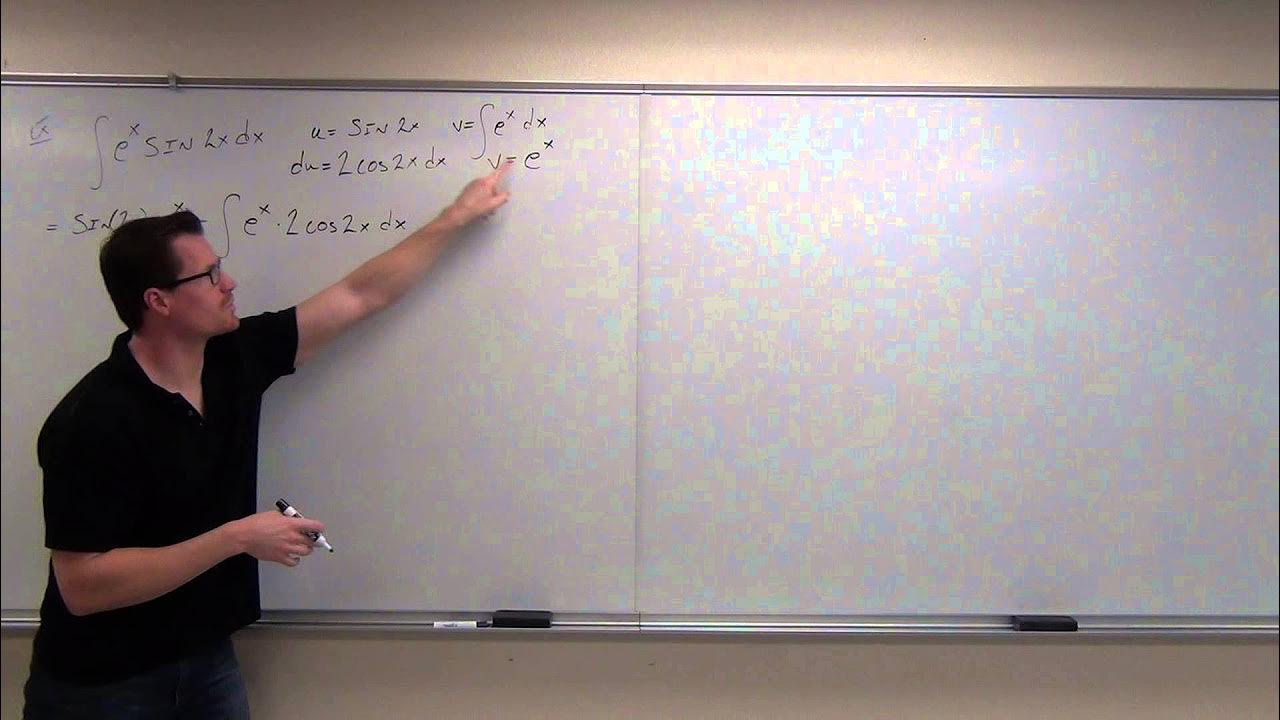Indefinite Integral - Basic Integration Rules, Problems, Formulas, Trig Functions, Calculus
TLDRThis video script is a comprehensive guide to solving indefinite integral problems. It covers the integration of constants, variables, polynomials, and functions involving exponents and roots. The script introduces various techniques such as u-substitution, integration by parts, and trigonometric substitution, providing clear examples for each method. It also touches on the anti-derivatives of trigonometric functions and exponential functions, offering a solid foundation for those looking to understand or review integral calculus.
Takeaways
- 📚 The integral of a constant multiplied by dx is the constant times x plus a constant (C).
- 🔄 When integrating a variable to a constant power, use the power rule: ∫x^n dx = x^(n+1)/(n+1) + C.
- 🌟 For square root and cube root functions, rewrite the root as a fractional exponent before applying the power rule.
- 📈 To find the antiderivative of polynomial functions, integrate each term separately and combine the results.
- 🔢 When integrating a function with a linear exponent in the denominator, rewrite the fraction and apply the power rule to the numerator.
- 🌀 For exponential functions, if the base is a linear function of x, the antiderivative is the function itself divided by the derivative of the exponent.
- 📊 Trigonometric functions' derivatives and antiderivatives are related; the antiderivative of cosine is sine/n and vice versa, with adjustments for the coefficient and angle.
- 🧠 U-substitution is a technique used when integrating a product of the function and its derivative; replace the variable with a new one (u) and solve for the new derivative (du/dx).
- 🔍 Integration by parts is applicable when u and dv are chosen such that their derivatives and antiderivatives can cancel each other out.
- 📐 Trigonometric substitution is useful for integrals involving 1 + x^2 or similar patterns, by replacing x with a trigonometric function of a new variable (θ).
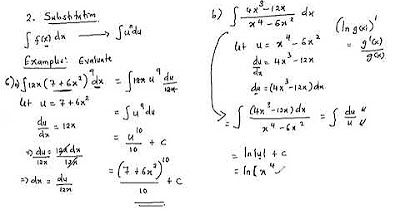
- 🛠️ Special cases like integrating 1/x require recognizing the function as the derivative of ln|x| and applying the natural logarithm as the antiderivative.
Q & A
What is the integral of 4 dx?
-The integral of 4 dx is 4x + C, where C is the constant of integration.
How do you find the antiderivative of a constant, such as pi?
-The antiderivative of a constant, such as pi, is simply pi times the variable, so in this case, it would be pi*y + C.
What is the formula for the antiderivative of x raised to the power of n?
-The antiderivative of x raised to the power of n is (x^(n+1))/(n+1) + C.
How do you find the antiderivative of a polynomial function like x^2 - 5x + 6?
-To find the antiderivative of a polynomial function, you integrate each term separately. For x^2 - 5x + 6, the antiderivative is (x^3)/3 - (5x^2)/2 + 6x + C.
What is the antiderivative of the square root of x?
-The antiderivative of the square root of x is (2/3)*x^(3/2) + C, after rewriting the square root as x^(1/2) and applying the power rule.
How do you use u-substitution to find the antiderivative of x^2 * sin(x^3) dx?
-For x^2 * sin(x^3) dx, you would use u-substitution by setting u = x^3. Then, du = 3x^2 dx, and dx = du/(3x^2). The integral becomes (1/3) * sin(u) du, which simplifies to (-1/3) * cos(u) + C. Finally, replace u with x^3 to get the final answer: (-1/3) * cos(x^3) + C.
What is the antiderivative of tangent(x)?
-The antiderivative of tangent(x) is ln(secant(x)) + C, which can also be written as ln(1/cosine(x)) + C.
How do you apply integration by parts to find the antiderivative of x * e^(4x) dx?
-For x * e^(4x) dx, you would use integration by parts with u = x and dv = e^(4x) dx. Then, du = dx and v = (1/4) * e^(4x). Applying the integration by parts formula, the antiderivative is (1/4) * x * e^(4x) - (1/16) * e^(4x) + C.
What is the antiderivative of 4/(1 + x^2) dx?
-The antiderivative of 4/(1 + x^2) dx is 4 * arctan(x) + C, after using the trigonometric substitution where x = tan(θ) and dx = sec^2(θ) dθ.
How do you find the antiderivative of a function with a complex denominator like (4/(1+x^2)^(3/2) dx)?
-For (4/(1+x^2)^(3/2) dx), you would first simplify the denominator by recognizing that (1+x^2)^(3/2) is the square of (1+x^2)^(1/2), which is secant squared. Then, using trigonometric substitution with x = tan(θ), you would rewrite the integral in terms of secant and tangent, and integrate to get the antiderivative.
What is the antiderivative of x * cos(x) dx using integration by parts?
-Using integration by parts with u = x and dv = cos(x) dx, where du = dx and v = sin(x), the antiderivative of x * cos(x) dx is x * sin(x) - integral of sin(x) dx, which simplifies to x * sin(x) + cos(x) + C.
Outlines
📚 Fundamental Indefinite Integrals
This paragraph introduces the concept of indefinite integrals, emphasizing the importance of the constant 'c' in anti-derivatives. It explains how to find the anti-derivative of constants and variables, including raising a variable to a constant power. The paragraph provides examples such as the integral of 4 dx, pi dy, and e dz, and illustrates the process of integrating polynomial functions and square root functions, highlighting the technique of adding one to the exponent and dividing by the result plus one.
🔍 Advanced Integration Techniques
The second paragraph delves into more complex integration techniques, including the use of the FOIL method for polynomials and the integration of fractional functions. It covers the anti-derivative of cube and square root functions, and introduces the concept of rewriting fractions with a single term in the denominator. The paragraph also explains the process of integrating functions like 1/x^2 and 1/x^3, emphasizing the use of power rules and the final simplification of the results.
🌐 Exponential and Trigonometric Integrals
This paragraph focuses on the anti-derivative of exponential and trigonometric functions. It explains the process of integrating exponential functions where the exponent is a linear function, such as e^(4x) and e^(x), and highlights the anti-derivative of trigonometric functions like cosine and sine. The paragraph also introduces the technique of u-substitution for more complex integrals involving sine and cosine functions.
🧩 Integration by Parts and Trigonometric Substitution
The fourth paragraph discusses the integration by parts method, providing a formula and examples of its application, such as the integral of x times cosine x and x times e^(4x). It also introduces trigonometric substitution for integrals involving 1 + x^2 and 1 - sin^2(x), explaining how to replace variables and solve for the anti-derivative using identities like 1 + tan^2(x) = sec^2(x) and sin^2(x) + cos^2(x) = 1.
📈 Special Integrals and Substitution Techniques
The final paragraph explores special integrals that do not fit into the previous categories, such as the anti-derivative of 1/x and the use of trigonometric substitution for integrals involving 1 + x^2. It explains how to apply these techniques to solve complex integrals, including the process of replacing variables and solving for the anti-derivative, ultimately providing the final answers in terms of the original variables.
Mindmap
Keywords
💡Indefinite Integral
💡Antideriviative
💡Constant of Integration
💡Power Rule
💡Polynomial Functions
💡Trigonometric Functions
💡Exponential Functions
💡Integration Techniques
💡Integration by Parts
💡Trigonometric Substitution
💡U-Substitution
Highlights
The integral of a constant is the constant times x plus C.
The antiderivative of pi with respect to y is pi*y + C.
The antiderivative of e with respect to z is e*z + C.
For integrating a variable raised to a constant, use the formula (x^n) = (x^(n+1))/(n+1) + C.
The antiderivative of x^2 dx is (1/3)x^3 + C.
The antiderivative of x^3 is (1/4)x^4 + C.
For 8x^3, the antiderivative is 2x^4 + C after simplifying the constant factor.
The antiderivative of 5x^6 is (5/7)x^7 + C after applying the power rule.
For a polynomial function, integrate each term separately, e.g., for x^2 - 5x + 6, the antiderivative is (1/3)x^3 - (5/2)x^2 + 6x + C.
The antiderivative of the square root of x is (2/3)x^(3/2) + C.
The antiderivative of the cube root of x^4 is (3/7)x^(7/3) + C.
For 3x - 1 squared, use FOIL to expand and then integrate each term.
The antiderivative of 2x + 1 times x - 2 is 2x^3/3 - 3x^2/2 - 2x + C after applying the distributive property and integrating.
For x^4 + 6x^3/x, separate the terms over x and integrate to get (1/4)x^4 + 6x^2/3 + C.
The antiderivative of 1/x^2 is -1/x + C, using the rule for integrating a function of the form 1/x^n.
The antiderivative of e^(4x) is e^(4x)/4 + C, using the rule for integrating exponential functions with a linear exponent.
The antiderivative of cos(x) is sin(x)/n + C, where n is the coefficient of x in the original function.
The antiderivative of sec^2(x) dx is tan(x), using the relationship between the derivative of tangent and secant squared.
For x^2 sin(x^3) dx, use u-substitution with u = x^3 and du = 3x^2 dx to find the antiderivative - (1/3)cos(x^3) + C.
For (x^2 + 3x)^5 dx, use u-substitution with u = x^2 + 3x and du = (2x + 3)dx to find the antiderivative (1/2)x^2 + 3x + C.
The antiderivative of tan(x) is ln(sec(x)) + C, using u-substitution with u = cos(x) and du = -sin(x)dx.
For x*cos(x) dx, use integration by parts with u = x and dv = cos(x)dx to find the antiderivative x*sin(x) + cos(x) + C.
For 4/(1+x^2) dx, use trigonometric substitution with x = tan(θ) and dx = sec^2(θ)dθ to find the antiderivative 4*arctan(x) + C.
For 1 - sin^2(x) dx, use the identity 1 - sin^2(x) = cos^2(x) and trigonometric substitution to find the antiderivative 3*asin(x) + C.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: