How many oz of 5% acid and 20% acid must be mixed to get 10 oz of a solution that is 12.5% acid?
TLDRIn this instructional video, math teacher John tackles a challenging algebraic word problem involving the mixing of 5% and 20% acid solutions to create a 12.5% acid mixture. He emphasizes the importance of understanding mixture problems and provides a step-by-step breakdown of the process, including setting up a system of linear equations and using the elimination method to solve for the unknown quantities. John's clear explanation and emphasis on algebraic skills make this a valuable resource for students struggling with similar problems.
Takeaways
- 📝 The problem involves mixing two solutions, a 5% acid and a 20% acid, to create a 12.5% acid solution in a total volume of 10 ounces.
- 🔢 The script provides the correct answer, which is 5 ounces of the 5% solution and 5 ounces of the 20% solution.
- 🎓 The problem is a classic algebraic mixture problem, typically found in middle and high school math courses.
- 👨🏫 The speaker, John, has decades of experience teaching math and aims to make learning math easier.
- 🌐 John promotes his math help program at TCM academy.com for those needing further assistance.
- 📚 The importance of reading and understanding the problem is emphasized, as well as visualizing the situation through a model.
- 🔍 The problem requires setting up a system of two linear equations with two variables, x and y, representing the ounces of the 5% and 20% solutions.
- 📱 The process involves finding the amount of acid in each solution, which is calculated by multiplying the percentage by the total ounces of the solution.
- 🧩 The equations are combined using either the substitution or elimination method to solve for the variables x and y.
- 🎉 The speaker encourages celebrating the correct solution and emphasizes the importance of mastering algebraic skills for academic success.
- 🔗 The speaker provides links to his Algebra 1 and Algebra 2 courses for additional practice and understanding of algebraic concepts.
Q & A
What is the main problem being discussed in the transcript?
-The main problem is about mixing two different concentrations of acid to create a 10-ounce solution with a 12.5% acid concentration.
What are the concentrations of the two acids mentioned in the problem?
-The two acids mentioned are 5% and 20% concentrations.
What is the desired concentration of the final mixture?
-The desired concentration of the final mixture is 12.5% acid.
How many ounces of the final mixture are required?
-The required amount of the final mixture is 10 ounces.
What is the solution to the mixture problem?
-The solution is to mix 5 ounces of the 5% acid solution with 5 ounces of the 20% acid solution to get a 10-ounce solution with a 12.5% acid concentration.
What type of math problem does this fall under?
-This problem falls under the category of mixture problems in algebra.
What are the two unknown variables in the problem?
-The two unknown variables are x (ounces of the 5% acid solution) and y (ounces of the 20% acid solution).
How many equations are needed to solve for two variables?
-To solve for two variables, you typically need two equations.
What is the first step in solving the problem?
-The first step is to define the variables (x for the 5% solution and y for the 20% solution) and set up a table to organize the information.
What method is used to solve the system of equations?
-The elimination method is used to solve the system of equations.
What is the significance of the teacher's introduction in the transcript?
-The teacher's introduction provides context about his experience and offers additional resources for learning math, indicating his passion for teaching and helping students understand math concepts.
Outlines
📚 Introduction to the Algebraic Mixture Problem
The video begins with an introduction to an algebraic word problem involving the mixing of acids with different concentrations. The problem at hand is to determine the quantities of 5% and 20% acid solutions needed to create a 10-ounce solution with a 12.5% acid concentration. The speaker, John, a middle and high school math teacher, encourages viewers to attempt the problem and engage with the content. He also promotes his math help program at TCM academy.com and emphasizes the importance of understanding mixture problems for students taking algebra and related courses.
🤔 Breaking Down the Mixture Problem
In this paragraph, John breaks down the mixture problem, explaining the need to balance the quantities of 5% and 20% acid solutions to achieve the desired 12.5% concentration in a 10-ounce mixture. He emphasizes the importance of understanding the problem and the need to be patient when tackling such algebraic word problems. John also introduces the concept of setting up a model to visualize the problem, highlighting that the challenge lies in finding the right balance between the two solutions to achieve the target concentration.
📝 Setting Up the Algebraic Equations
John proceeds to define the variables for the problem, letting x represent the ounces of the 5% acid solution and y represent the ounces of the 20% solution. He then explains the need for two equations to solve for these two unknowns, as one equation is insufficient. He introduces the concept of a system of linear equations and emphasizes the importance of algebra skills in solving such problems. John also provides a brief overview of how to approach solving the system, mentioning techniques like the substitution and elimination methods.
🔢 Solving the System of Equations
The speaker continues by explaining how to solve the system of equations. He suggests multiplying the equations to eliminate decimals and make the calculations easier. John then demonstrates the process of using the elimination method to solve the system, resulting in finding that 5 ounces of the 5% solution and 5 ounces of the 20% solution are needed to create the desired 10-ounce 12.5% acid mixture. He emphasizes the importance of understanding how to solve systems for students learning algebra and related mathematical concepts.
🎉 Conclusion and Encouragement
In the final paragraph, John concludes the solution to the algebraic mixture problem, reiterating the need for understanding systems of equations for students learning algebra. He encourages viewers to like and subscribe to his channel for more comprehensive math explanations and assistance. John also offers his support as a math teacher through his online courses and reiterates the importance of practice and patience in mastering algebraic problem-solving skills.
Mindmap
Keywords
💡Algebra
💡Mixture Problem
💡Percentage
💡Ounce
💡System of Equations
💡Variables
💡Linear Equations
💡Elimination Method
💡Substitution Method
💡Mathematics Teacher
💡Educational Video
Highlights
The problem involves mixing 5% and 20% acid solutions to create a 12.5% acid solution.
The goal is to find out how many ounces of each solution are needed to make 10 ounces of the 12.5% solution.
The problem requires algebra skills to set up and solve a system of linear equations.
Let x be the ounces of the 5% solution and y be the ounces of the 20% solution.
The total ounces of the mixture must equal 10, so x + y = 10.
The amount of acid in the 5% solution is 0.05x and in the 20% solution is 0.20y.
The total acid content in the 10 oz mixture should be 12.5%, or 0.125 * 10.
This leads to the second equation: 0.05x + 0.20y = 0.125 * 10.
The system of equations is x + y = 10 and 5x + 20y = 125.
To solve the system, one can use either the substitution method or the elimination method.
Multiplying the second equation by 100 simplifies it to 5x + 20y = 125.
By using the elimination method, we multiply the first equation by -5 and add it to the second to eliminate x.
This results in the simplified equation 15y = 75.
Solving for y gives us y = 5, which means we need 5 ounces of the 20% solution.
Substituting y back into the first equation gives us x = 5, indicating we also need 5 ounces of the 5% solution.
The solution to the problem is to mix 5 ounces of the 5% acid solution with 5 ounces of the 20% acid solution to get a 12.5% solution.
This problem is a classic type of mixture problem in algebra, essential for students in algebra courses.
The problem requires understanding of systems of linear equations, a fundamental algebra skill.
Once the problem is solved, it demonstrates the ability to apply algebra to real-world scenarios, such as mixing solutions.
Transcripts
Browse More Related Video

Mixture Problems

Algebra SYSTEM WORD PROBLEM – Let’s solve it step-by-step...
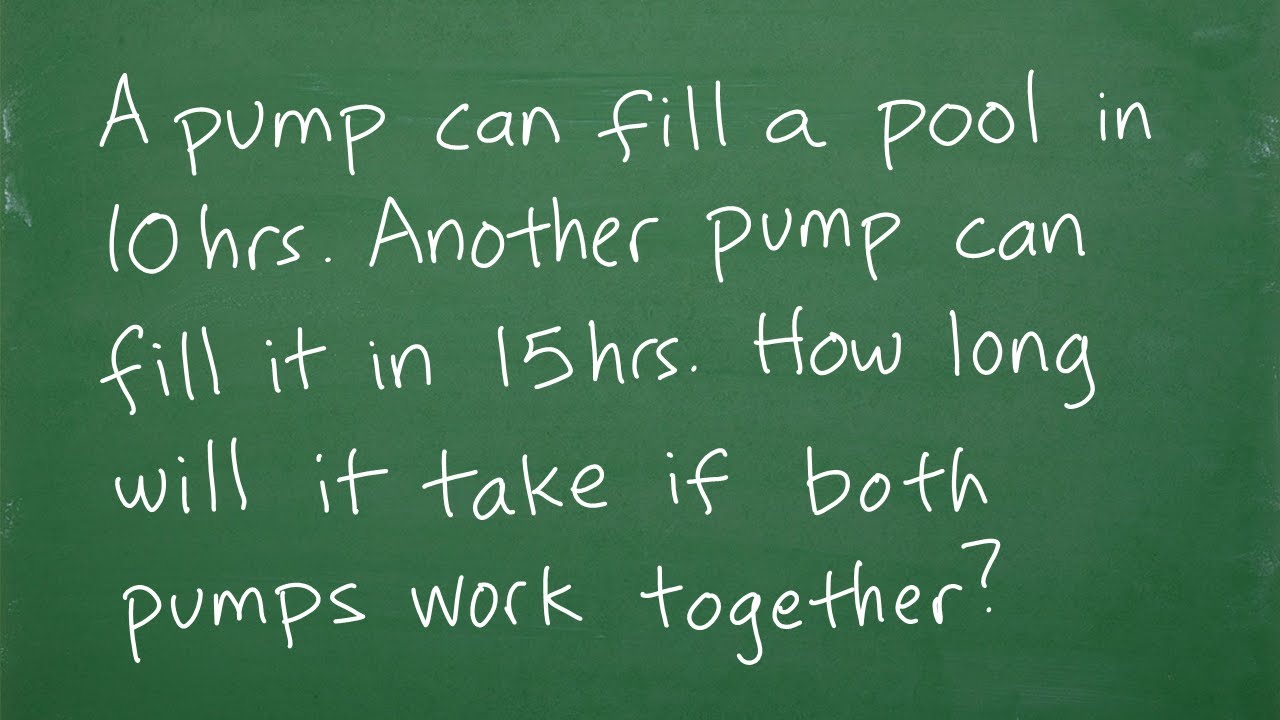
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

3/2(x + 4) = 5 – 1/3(4 – x), many don’t know the EASY way to solve!

The Algebra Step that EVERYONE Gets WRONG!
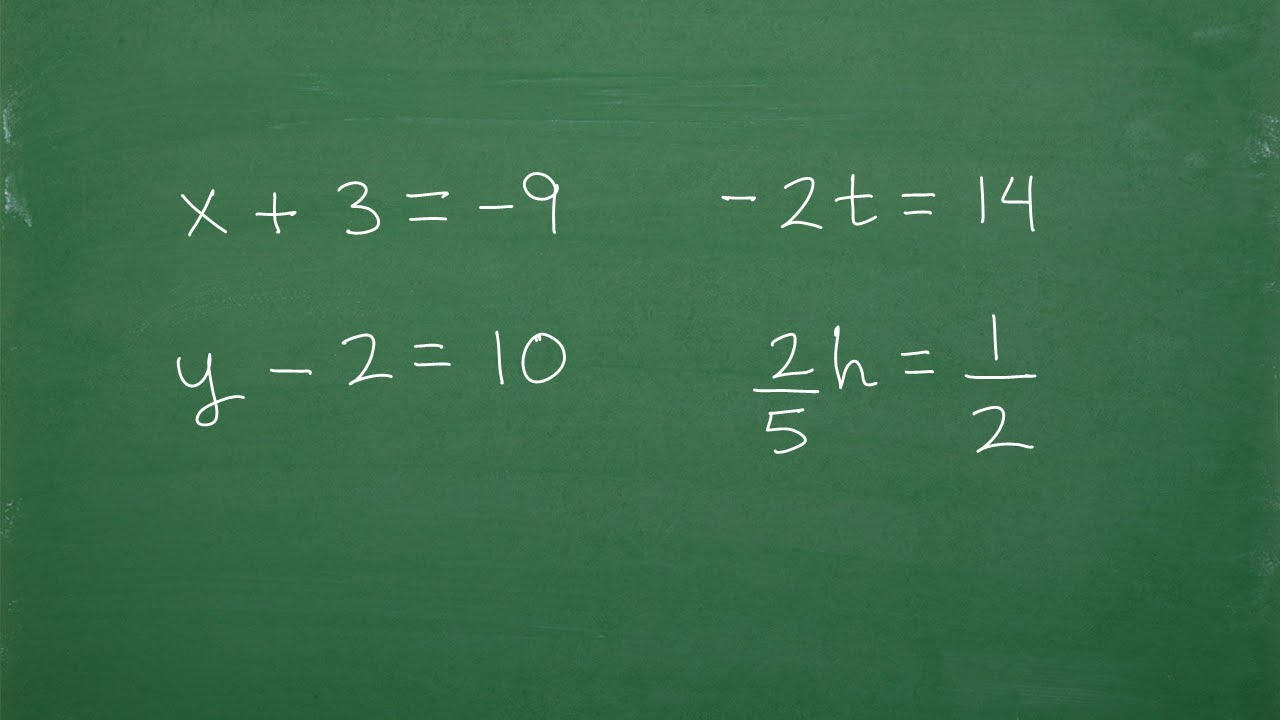
Let’s Solve These Basic Algebra Equations- Step-by-Step…….
5.0 / 5 (0 votes)
Thanks for rating: