Calculus Notation & Terminology
TLDRThe script discusses the concept of differentiation in mathematics, explaining the various notations and terminologies associated with it. It clarifies the process of finding the gradient function or derivative of a given function, emphasizing the use of 'f dash' to denote the derivative. The importance of context, such as 'rise over run' for gradient, and the correct application of 'd on dx' notation are highlighted. The script also touches on the specificity of differentiation at a particular point and the flexibility of variable representation across different fields.
Takeaways
- 📈 Differentiation is the process of finding the gradient function of a given function.
- 🔄 The gradient function is also known as the derivative, which is derived from the original function.
- 🎓 The process of finding the derivative is called 'differentiating', not 'deriving'.
- 📊 The gradient (or derivative) represents the rate of change in the function, often described as 'rise over run'.
- 📐 The 'rise over run' concept can be mathematically represented as the change in y (Δy) over the change in x (Δx).
- 🅰️ In mathematical notation, the derivative is denoted as 'd/dx', where 'd' stands for 'delta', a Greek letter representing change.
- 📌 When differentiating, it's important to specify the function and the variable with respect to which differentiation is being done.
- 📍 Different notations are used for differentiation across various fields, such as mathematics, science, and engineering.
- 🔢 The choice of variable names (like x, y, p, v) doesn't affect the process of differentiation, but the notation must be clear and consistent.
- 🎯 When finding the gradient at a specific point, the notation often changes to reflect the value of the variable (e.g., f'(0) for the gradient at x=0).
Q & A
What is the process of finding the gradient function of a given function?
-The process of finding the gradient function of a given function is called differentiation. It involves calculating the rate at which the function changes with respect to its variable, which is represented by the derivative.
What is another term used for the gradient function?
-Another term used for the gradient function is the derivative, which indicates that it is derived from the original function.
What does the term 'rise over run' represent in the context of gradients?
-In the context of gradients, 'rise over run' represents the ratio of the vertical change (rise) to the horizontal change (run). This is essentially the slope of the function at a particular point and is a fundamental concept in understanding gradients.
How is the change in a variable denoted in calculus?
-In calculus, the change in a variable is denoted using the Greek letter delta (Δ). For example, the change in y is written as Δy, and the change in x is written as Δx.
What is the significance of the notation d/dx when differentiating a function?
-The notation d/dx represents the process of differentiation with respect to the variable x. It is used to indicate that we are finding the derivative or gradient function of the given expression with respect to x.
Why is it important to specify the variable when writing the derivative?
-Specifying the variable when writing the derivative is important because it clarifies with respect to which variable the differentiation is being performed. This is especially crucial when dealing with multiple variables or more complex expressions.
What does it mean to find the gradient at a particular point?
-Finding the gradient at a particular point involves evaluating the derivative or the rate of change of the function at that specific value of the variable. This gives us the slope or the instantaneous rate of change at that point.
How does the notation change when differentiating with respect to a variable other than x?
-When differentiating with respect to a variable other than x, the notation changes to reflect the new variable. For example, if differentiating with respect to v, the notation would be d/dv, indicating the derivative with respect to v.
Why are there so many different notations in calculus?
-There are many different notations in calculus because the subject is used by a wide variety of professionals, including mathematicians, scientists, and engineers, each of whom may have their own preferred ways of representing concepts. These notations cater to the diverse needs and preferences of different fields.
What is the common mistake people make when writing the derivative of a function?
-A common mistake is writing the derivative as d/dx without specifying the function. The correct notation should include the function, for example, d/dx (x^2), to indicate that the derivative is being taken with respect to x and applied to the function x^2.
How can the concept of differentiation be applied to other fields beyond mathematics?
-Differentiation, or the concept of finding the rate of change, is a fundamental idea that can be applied to various fields. For instance, in physics, it can be used to analyze the rate of change of velocity in motion, or in chemistry, it can be used to understand the rates of chemical reactions.
Outlines
📚 Introduction to Differentiation and Notation
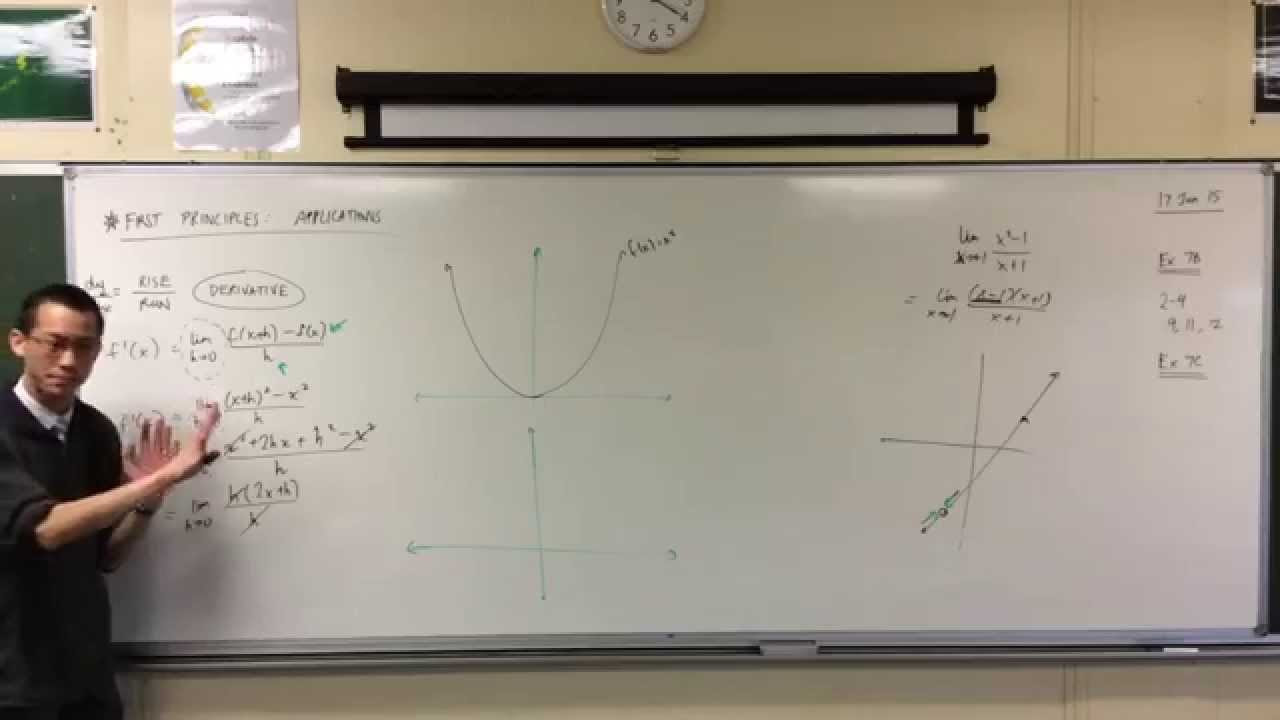
This paragraph introduces the concept of differentiation, explaining the various terminologies associated with it. The speaker aims to clarify the process of finding the gradient function, also known as the derivative, by breaking down the terms. The paragraph emphasizes the importance of understanding the notation, such as using 'f dash x' or 'f' with a prime to denote the gradient function. It also explains the concept of rise over run to describe the gradient, where 'rise' refers to the change in the y-value (∆y) and 'run' refers to the change in x (∆x). The use of 'dy' and 'dx' is introduced to represent these changes algebraically, and the importance of differentiating with respect to the variable of interest is highlighted.
🔢 Clarifications on Notation and Differentiation at Specific Points
The second paragraph delves into the nuances of differentiation notation and its application at specific points. It discusses how the gradient function is often denoted at a particular point, such as 'f dash zero' for the gradient at x=0. The paragraph also addresses the flexibility in variable notation, emphasizing that the letters used do not affect the underlying mathematical process. An example is given where the differentiation is applied to a position function with respect to velocity, using 'dp' and 'dv' instead of 'dy' and 'dx'. The paragraph acknowledges the various notations used across different fields, such as mathematics, science, and engineering, and attributes this to the diverse ways professionals in these fields prefer to represent the same concepts.
Mindmap
Keywords
💡Differentiation
💡Gradient Function
💡Derivative
💡Rise over Run
💡Delta (Δ)
💡d/dx
💡Function
💡Variable
💡Sine (sin)
💡Respect to
💡Position and Velocity
Highlights
Differentiation is a process used to find the gradient function of a given function.
The gradient function is also known as the derivative, which is derived from the original function.
The process of finding the derivative is called differentiating, not deriving, in mathematical terms.
The concept of gradient is related to the rise over run, which measures the rate of change in the vertical distance (y-value).
In mathematical notation, the change in y is represented as dy and the change in x as dx, which together define the gradient function.
When differentiating a function, it is important to specify the variable with respect to which the differentiation is being done.
The notation d/dx is used to denote the differentiation operator acting on a function.
When finding the derivative of a function like x squared, it is crucial to correctly apply the differentiation operator to the variable x.
At times, the derivative at a specific point is required, such as the gradient at x equals zero, denoted as f'(0).
Different fields, such as mathematics, science, and engineering, may use different notations for the concept of differentiation based on their context.
The notation 'with respect to' is often abbreviated to 'wrt' in mathematical expressions for convenience.
Differentiation can be applied to various types of functions, not just those involving y and x, but also other variables like position and velocity.
The differentiation process can be expressed in different ways, such as dy/dx or dp/dv, depending on the context and the variables involved.
The transcript emphasizes the importance of understanding the various notations and methods used in differentiation across different disciplines.
The concept of differentiation is fundamental to calculus and has wide-ranging applications in many scientific and technical fields.
The transcript provides a clear explanation of the terminology and notation used in differentiation, helping to demystify the subject for learners.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: