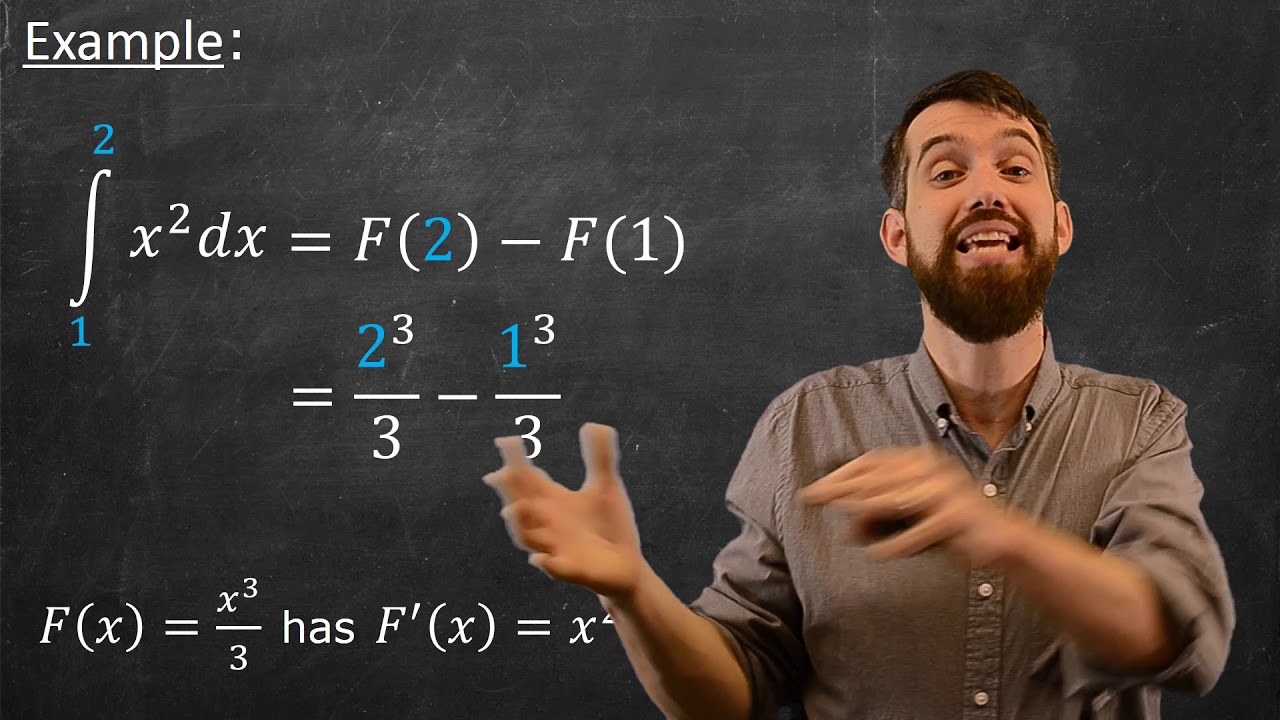What's the difference between a DEFINITE integral and an INDEFINITE integral? | CALCULUS
TLDRThe video script explains the key difference between indefinite and definite integrals in calculus. It clarifies that indefinite integrals lack specific limits, resulting in a family of functions, while definite integrals have limits of integration and yield a numerical value. The analogy is drawn to derivatives, where the indefinite integral is akin to a function (f prime of x) and the definite integral is like a specific value (f prime of 1). The video aims to help learners understand what to expect from the results of their integral calculations.
Takeaways
- 📚 The main difference between indefinite and definite integrals is that indefinite integrals lack specific limits of integration, while definite integrals include numerical or lettered (representing numbers) limits.
- 🔍 Indefinite integrals always result in a function (or family of functions), accounting for the 'plus C' (constant of integration), whereas definite integrals yield a specific numerical value.
- 📈 Definite integrals can be thought of as calculating the area between a curve and the x-axis for a specified interval, providing a concrete numerical answer.
- 🤔 When learning integrals, it's crucial to understand the context of the problem to determine whether an indefinite or definite integral is required.
- 🌟 The process of evaluating integrals often involves using the fundamental theorem of calculus, especially when transitioning from an indefinite to a definite integral.
- 📊 The concept of indefinite integrals is more general and flexible, as they do not commit to a specific region or interval for the integration.
- 🏢 Analogous to derivatives, indefinite integrals are to definite integrals what the derivative function (f'(x)) is to a specific derivative value (f'(1))
- 💡 The 'plus C' in indefinite integrals signifies that the answer can vary while still being correct, adding to the generality of the solution.
- 📖 Understanding the distinction between indefinite and definite integrals is key to solving calculus problems and interpreting their results accurately.
- 🎓 The video script serves as a guide for beginners in calculus, clarifying common confusions and providing insights into the nature of integrals.
- 👇 Encouraging engagement through comments for further clarification and guidance on integral-related topics demonstrates the script's aim to support learners in their calculus journey.
Q & A
What is the main difference between indefinite and definite integrals?
-Indefinite integrals do not have specific limits of integration and represent a family of functions, while definite integrals have numerical limits and yield a specific numerical value.
How can you identify an indefinite integral?
-An indefinite integral can be identified by the absence of numbers or specific variables representing numbers on the integral symbol; it will always equal a function, which may involve a constant 'plus C'.
How can you identify a definite integral?
-A definite integral is characterized by the presence of numbers or letters representing numbers on the integral symbol, indicating the specific limits of integration, and it will always equal a number.
What does an indefinite integral represent?
-An indefinite integral represents a general antiderivative or a family of functions, which is not specific to a particular area or value but can be used to find the function that, when differentiated, yields the original function.
What is the role of the 'plus C' in indefinite integrals?
-The 'plus C' in indefinite integrals signifies that there are infinitely many antiderivatives that can satisfy the integral, each differing by a constant. This is because the derivative of a constant is zero, allowing for the addition of any constant to the function.
How does a definite integral provide a specific answer?
-A definite integral provides a specific numerical answer by calculating the signed area between the curve and the x-axis for the given numerical limits of integration, which is a concrete and specific value related to a particular problem.
What is the relationship between indefinite integrals and the fundamental theorem of calculus?
-The fundamental theorem of calculus connects indefinite integrals with definite integrals by stating that if a function is continuous and has an antiderivative, then a definite integral can be calculated by evaluating the antiderivative at the limits of integration.
How is the concept of indefinite integrals analogous to derivatives?
-Just as the derivative of a function at a specific point (e.g., f'(1)) gives a concrete value (the slope at x=1), indefinite integrals provide a general function that can be used to find specific values when the limits of integration are specified.
What is the significance of understanding the difference between indefinite and definite integrals?
-Understanding the difference between indefinite and definite integrals is crucial for correctly interpreting the results of integration problems and applying them to various mathematical and real-world scenarios, such as calculating areas or solving differential equations.
Why might a problem be given as an indefinite integral rather than a definite one?
-A problem might be given as an indefinite integral when the specific limits of integration are not provided, requiring the solution to be a general function that can be applied to any interval. Once the limits are determined, the indefinite integral can be used to find the numerical answer using the fundamental theorem of calculus.
What are some common misconceptions about indefinite integrals?
-Some common misconceptions about indefinite integrals include the belief that they always represent a single function or that they can provide a specific numerical answer without specifying the limits of integration. In reality, indefinite integrals represent a family of functions and require additional information to yield a specific numerical result.
Outlines
📚 Understanding the Difference Between Indefinite and Definite Integrals
This paragraph introduces the fundamental distinction between indefinite and definite integrals in calculus. It explains that indefinite integrals lack specific numbers on the integral symbol, representing a family of functions due to the presence of 'plus C', while definite integrals have numerical values or letters representing numbers on the integral symbol, signifying the limits of integration. The speaker clarifies that definite integrals provide a concrete numerical answer, akin to finding a specific area under a curve between given bounds, whereas indefinite integrals remain general, representing a function. The analogy is drawn between this concept and the difference between a derivative function (f'(x)) and a specific derivative value (f'(1)), emphasizing the specificity of the latter in answering concrete questions.
Mindmap
Keywords
💡Calculus
💡Indefinite Integral
💡Definite Integral
💡Integral Symbol
💡Limits of Integration
💡Functions
💡Antiderivative
💡Area
💡Fundamental Theorem of Calculus
💡Derivatives
💡Slope
Highlights
The main difference between indefinite and definite integrals is that indefinite integrals lack numbers on the integral symbol, while definite integrals have numbers or letters representing numbers.
Definite integrals have limits of integration, which indefinite integrals do not.
A definite integral will always equal a number, whereas an indefinite integral will always equal a function or a family of functions due to the plus C (constant).
Definite integrals calculate the area between a curve and the x-axis for specific numbers, providing a concrete numerical answer.
Indefinite integrals provide a general answer, as they do not specify the range for which the area or quantity is being calculated.
The fundamental theorem of calculus can be used to convert an indefinite integral into a specific numerical answer once the limits of integration are defined.
Integral problems are typically given as either a definite integral or an indefinite integral, and understanding the difference helps to know what type of answer to expect.
The difference between indefinite integrals and definite integrals is analogous to the difference between a derivative function (f'(x)) and a specific derivative value (f'(1)).
A specific derivative value (like f'(1)) gives a concrete answer, such as the slope of a function at a particular point.
The concept of indefinite and definite integrals is a fundamental aspect of calculus, essential for understanding more advanced topics.
The process of integrating involves finding the original function that produced a given derivative, which is crucial for solving various calculus problems.
Understanding the distinction between indefinite and definite integrals helps in applying the correct approach to problem-solving in calculus.
The video aims to clarify the confusion often faced by students when learning about integrals for the first time.
The analogy between derivatives and integrals helps students to grasp the concepts more effectively by relating them to previously learned material.
The video encourages interaction by asking viewers to comment with their integral-related questions, fostering a community of learners.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: