AP Physics Workbook 7.K Rolling/Sliding/Both

Mr.S ClassRoom
21 Apr 202012:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the physics concepts of torque and rotation, focusing on the behavior of a wheel during a transition from sliding to rolling motion. It explains how the forces of gravity, normal force, and friction affect the wheel's center of mass speed and rotational speed. The script also clarifies a misconception in a derived equation, emphasizing the inverse relationship between the coefficient of friction and the period of rotation. The final motion of the wheel is described as rolling without slipping, reaching a linear speed of 1/2 V and an angular speed of 1/2 Omega. The impact of varying coefficients of friction on the wheel's velocity and angular velocity over time is also illustrated.

Takeaways
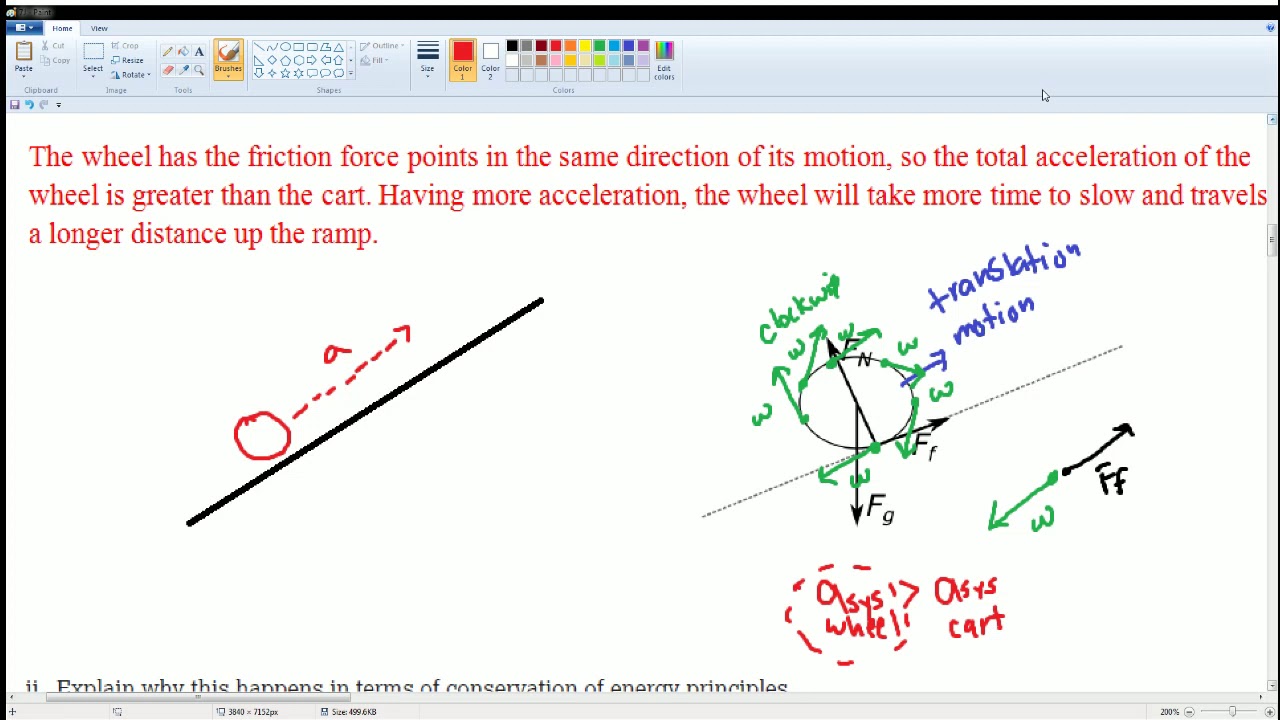
  • ๐Ÿ“Œ In a physics problem involving a rotating and sliding wheel, there are typically three forces at play: gravitational force, normal force, and frictional force.
  • ๐Ÿ”„ The velocity vector of the wheel is tangent to the wheel's motion and indicates the direction of rotation, which is clockwise in the given scenario.
  • ๐ŸŒ The angular velocity of the wheel is responsible for the rotation, and initially, the wheel spins within its initial angular velocity (Omega naught).
  • ๐Ÿš€ The center of mass of the wheel increases its speed due to the frictional force, which acts in the same direction as the desired motion, providing additional energy and acceleration.
  • ๐Ÿ”ฝ The linear speed of the wheel's center of mass increases as the wheel begins to roll without slipping, and the wheel's rotation speed decreases.
  • โฑ๏ธ The period of the wheel's rotation (T) is inversely related to the coefficient of friction (mu). As mu increases, the period decreases, and vice versa.
  • ๐Ÿ“‰ The frictional force acts counterclockwise, opposing the wheel's clockwise rotation, and causes the rotational speed to slow down over time.
  • ๐Ÿ›ค๏ธ The final motion of the wheel, regardless of the radius or coefficient of friction, is to roll without slipping, with a linear speed of 1/2 V (final) and an angular speed of 1/2 Omega (final).
  • ๐Ÿ•ฐ๏ธ A wheel on a surface with a low coefficient of friction will take more time to reach the final linear speed of 1/2 V (final) compared to a wheel on a surface with a high coefficient of friction.
  • ๐Ÿ“Š The graph illustrating the scenario shows that both high and low coefficients of friction lead to the same final speeds, but the time taken to reach those speeds differs, with higher friction requiring less time.
Q & A

  • What are the three forces acting on the wheel as described in the script?

    -The three forces acting on the wheel are gravitational force (downwards), normal force (opposite to gravitational force), and frictional force (opposite to the direction of velocity).

  • How does the velocity vector of the wheel influence the direction of the frictional force?

    -The velocity vector is tangent to the wheel's rotation and since the wheel is rotating clockwise, the frictional force must act in the opposite direction to oppose the motion, which is to the right.

  • Why does the center of mass of the wheel increase its speed during the time from T to Big T?

    -The center of mass of the wheel increases its speed because the frictional force, acting in the same direction as the wheel's translational motion, supplies additional energy, thus increasing the acceleration and speed of the center of mass.

  • What happens to the wheel's rotational speed as it moves from T to Big T?

    -The wheel's rotational speed decreases during this time due to the frictional force, which acts in a counterclockwise direction, opposing the wheel's initial clockwise rotation.

  • How does the coefficient of friction appear in the equation for the period of a rotating object?

    -The coefficient of friction appears in the denominator of the equation for the period of a rotating object. An increase in the coefficient of friction would result in a decrease in the period, as it would require less time to cover the same distance due to greater frictional force.

  • What is the final linear speed of the wheel when it rolls without slipping?

    -The final linear speed of the wheel when it rolls without slipping is 1/2 V_nought, where V_nought is the initial linear speed.

  • What is the final angular speed of the wheel when it rolls without slipping?

    -The final angular speed of the wheel when it rolls without slipping is 1/2 Omega_nought, where Omega_nought is the initial angular speed.

  • How does a low coefficient of friction affect the time taken for the wheel to reach its final speed?

    -A low coefficient of friction will require more time for the wheel to reach its final speed of 1/2 V_nought because the frictional force is less, leading to a slower deceleration of the wheel's rotational speed and a slower increase in its translational speed.

  • How does a high coefficient of friction affect the wheel's rotational speed decrease?

    -A high coefficient of friction will cause the wheel's rotational speed to decrease more quickly because the frictional force is greater, leading to a faster deceleration of the wheel's rotation and a quicker transition to rolling without slipping.

  • What is the relationship between the coefficient of friction and the time required for the wheel to cover a certain distance?

    -The coefficient of friction has an inverse relationship with the time required to cover a certain distance. Higher friction (greater mu) results in less time needed to cover the distance, while lower friction (smaller mu) results in more time needed.

Outlines
00:00
๐Ÿ“š Introduction to Torque and Rotation

This paragraph introduces the topic of the video, which is focused on unit 7 of the AP Physics workbook, covering torque, rotation, and the dynamics of a wheel in motion. It sets the scene for the analysis by describing a scenario where a wheel is released from rest and begins to rotate and slide on a surface. The paragraph outlines the forces at play, including gravity, normal force, and friction, and explains how these forces affect the wheel's motion. The importance of understanding the relationship between linear and angular velocity is emphasized, as well as the role of friction in increasing the translational speed of the wheel's center of mass. The video aims to help viewers grasp the concepts of how forces and velocities interact during the wheel's motion, and how friction can both increase linear speed and decrease rotational speed.

05:02
๐Ÿ“ Equation Analysis and Friction's Impact

This paragraph delves into the analysis of the equation that describes the period of a rotating object, highlighting the role of the coefficient of friction within the equation. It explains how an increase in the coefficient of friction would theoretically affect the period, but points out an error in the equation's current form. The correct relationship is discussed, emphasizing that the coefficient of friction should be in the denominator, indicating an inverse relationship between friction and the period of rotation. The paragraph uses a practical example of running on different surfaces to illustrate this concept, showing that increased friction leads to a longer time to cover the same distance. The summary also touches on how the final motion of the wheel is affected by the coefficient of friction, with the wheel eventually rolling without slipping.

10:02
๐Ÿ“Š Graph Analysis of Friction and Velocity

In this paragraph, the focus shifts to the analysis of graphs that illustrate the effects of different coefficients of friction on the wheel's linear and angular velocities. It explains how a low coefficient of friction would require more time for the wheel to reach a linear speed of half its initial value, while a high coefficient of friction would require less time. The paragraph also discusses the changes in angular velocity, noting that it decreases over time as the wheel transitions from sliding to rolling. The summary provides a visual representation of these concepts through the description of the graphs, emphasizing the final velocities of the wheelโ€”half of the initial linear and angular velocities. The paragraph concludes by reiterating the impact of the coefficient of friction on the time it takes for the wheel to reach its final state of motion.

Mindmap
Keywords
๐Ÿ’กTorque
Torque is a measure of the rotational force acting on an object. In the context of the video, it is the force that causes the wheel to rotate. It is related to the main theme as it is a fundamental concept in understanding the physics of rotation and is used to explain how the wheel's motion changes when it interacts with different forces.
๐Ÿ’กRotation
Rotation refers to the motion of an object turning around a fixed axis. In the video, the wheel's rotation is central to the discussion, as it is affected by various forces such as gravity, normal force, and friction. The wheel's rotational motion is analyzed in terms of its velocity and angular velocity, which are key to understanding the dynamics of the system.
๐Ÿ’กFriction
Friction is the resistive force that opposes the relative motion of two surfaces in contact. In the video, friction plays a crucial role in determining the wheel's motion, affecting both its linear and rotational speeds. The force of friction is depicted as a key factor that causes the wheel to eventually roll without slipping.
๐Ÿ’กAngular Velocity
Angular velocity is the rate at which an object rotates, measured in terms of the angle covered per unit of time. In the video, the angular velocity of the wheel is a central concept used to describe its rotational motion. The changes in angular velocity are analyzed in relation to the forces acting on the wheel and how these forces lead to a transition from sliding to rolling motion.
๐Ÿ’กLinear Speed
Linear speed is the rate at which an object moves along a straight path. In the video, the linear speed of the wheel's center of mass is discussed in relation to the frictional force. The wheel's linear speed increases as it transitions from sliding to rolling, which is a direct result of the frictional force acting on it.
๐Ÿ’กCenter of Mass
The center of mass is the point at which the mass of an object is concentrated for the purpose of analyzing its motion. In the video, the center of mass of the wheel is relevant because it is the point around which the wheel rotates and also moves linearly when the wheel starts rolling.
๐Ÿ’กVelocity Vector
A velocity vector is a vector quantity that represents the speed and direction of an object's motion. In the video, the velocity vector is used to describe the direction of the wheel's motion, which is tangential to the circle formed by the rotating wheel.
๐Ÿ’กCoefficient of Friction
The coefficient of friction is a dimensionless number that represents the frictional properties between two surfaces. In the video, the coefficient of friction is crucial in determining the period of the wheel's rotation and how quickly the wheel's rotational speed decreases.
๐Ÿ’กPeriod
The period is the duration of one complete cycle of motion in a periodic system. In the context of the video, the period refers to the time it takes for the wheel to complete one full rotation. The script explains how the period is affected by the coefficient of friction and the wheel's motion.
๐Ÿ’กRolling Without Slipping
Rolling without slipping is a type of motion where an object moves in such a way that its point of contact with the surface does not slide, but rather, the object rotates about its own axis. In the video, this concept is important as it describes the final state of the wheel's motion after it has been acted upon by various forces.
๐Ÿ’กEquations
Equations are mathematical statements that assert the equality of two expressions. In the video, equations are used to model and predict the behavior of the wheel under different forces. They are essential for understanding the quantitative aspects of the wheel's motion and the effects of friction.
Highlights

The scenario involves a wheel rotating and then transitioning from sliding to rolling without slipping.

The force of gravity acts downward on the wheel.

The normal force is opposite to the force of gravity.

Friction force is in the opposite direction to the velocity of the wheel.

The velocity vector is tangent to the wheel's motion and the angular velocity is the velocity at the edge of the wheel.

The center of mass of the wheel increases its speed due to the friction force.

The wheel spins with an initial angular velocity (Omega naught) and the center of the wheel has an initial linear speed (V naught) of zero.

As the wheel falls and hits the floor, it starts to move forward while its rotation speed decreases.

The friction force increases the wheel's translational speed by providing more energy.

The frictional force and torque cause the rotational speed of the wheel to slow down.

The equation provided in the transcript relates the period of a rotating object to the coefficient of friction.

An increase in the coefficient of friction leads to a decrease in the period of the rotating object.

The final motion of the wheel is to roll without slipping, with a linear speed of 1/2 V and an angular speed of 1/2 Omega.

The coefficient of friction affects the time it takes for the wheel to reach its final speed; a higher coefficient results in less time required.

The friction force has an inverse relationship with the period of the rotating object; as one increases, the other decreases.

The graph illustrates the relationship between the coefficient of friction, linear speed, and angular velocity over time.

The wheel's linear speed increases and then decreases to a final speed of 1/2 V naught, while its angular velocity decreases from its initial value to 1/2 Omega naught.

The theoretical explanation provided in the transcript helps to understand the dynamics of a wheel transitioning from sliding to rolling.

Transcripts

Browse More Related Video

2016 #1 Free Response Question - AP Physics 1 - Exam Solution

Pure Rolling Motion | Physics with Professor Matt Anderson | M12-12

2016 AP Physics 1 Free Response #1

AP Physics Workbook 7.J Translation vs Rotation

Rotational Kinematics Physics Problems, Basic Introduction, Equations & Formulas

Angular Momentum of a Spinning Wheel | Physics with Professor Matt Anderson | M12-16

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsWorkbookTorqueAnalysisRotationalSpeedFrictionalForceAccelerationWheelDynamicsAPPhysicsMechanicalEnergyEducationalContentScienceEducation