2016 AP Physics 1 Free Response #1
TLDRIn this educational video, Alan from Bothell STEM Coach dissects a 2016 AP Physics 1 free response question involving a wooden wheel rolling down a ramp under the influence of gravity, friction, and the normal force. He explains the forces at play, derives an expression for the wheel's acceleration, and compares its descent to a block of ice on the same ramp with negligible friction. Alan emphasizes the impact of rotational energy on the wheel's kinetic energy, concluding that the block reaches the bottom with greater speed due to less energy conversion to rotation.
Takeaways
- 📚 Alan introduces a free response question from the 2016 AP Physics 1 exam, focusing on the forces acting on a wooden wheel rolling down a ramp.
- 🔍 The wooden wheel experiences gravity, static friction, and the normal force from the ramp as it rolls down the inclined plane.
- 📏 The forces are to be labeled on a diagram with distinct arrows, indicating the point of application and direction without necessarily showing the relative magnitudes.
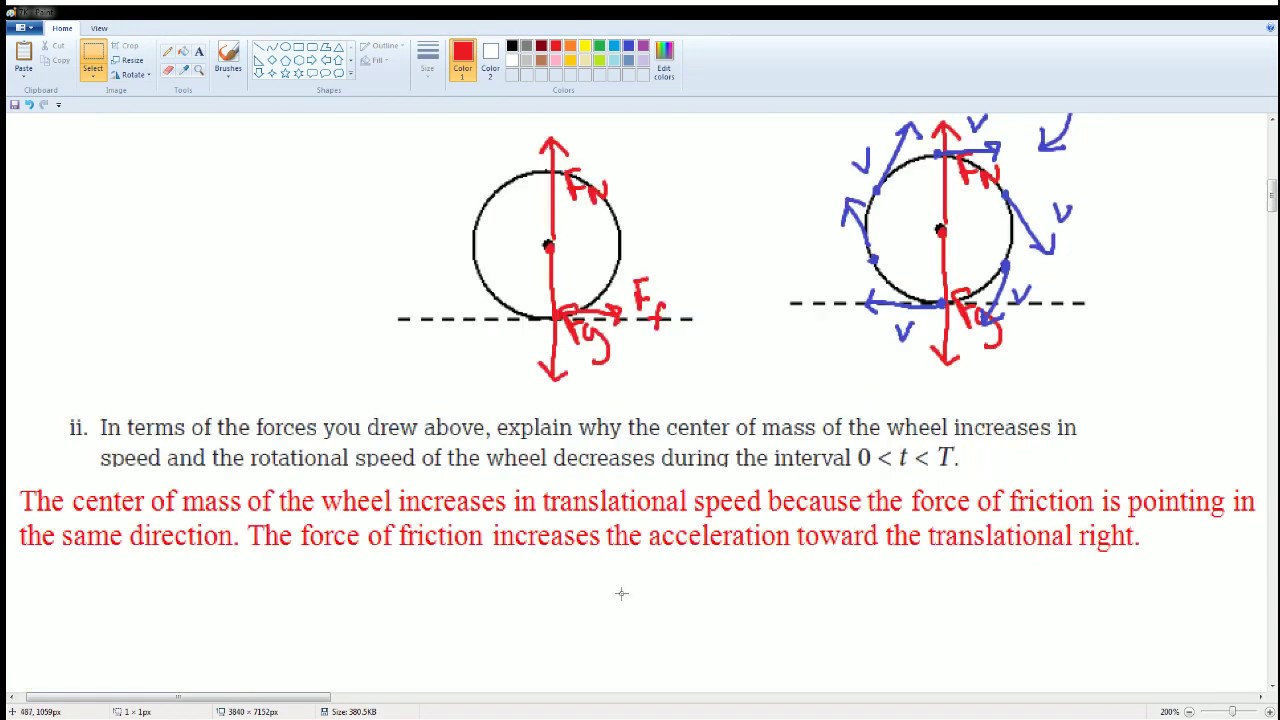
- 🌀 The only force causing a change in the wheel's angular velocity is the frictional force, which exerts a non-zero torque.
- ⚖️ The frictional force is calculated as 40% of the component of gravitational force opposing the motion, which is mg sine theta.
- 📉 The wheel's acceleration is derived by balancing the forces along the ramp and considering the frictional force as a percentage of the maximum static friction.
- 🔄 The wheel's rotation requires energy, which is a part of the potential energy converted from the gravitational potential energy.
- 🚀 In a comparison with a block of ice sliding down the same ramp with negligible friction, the block reaches the bottom with a greater speed due to less energy being used for rotation.
- 🤓 Alan provides an explanation of the energy conversion process, emphasizing that the wheel loses some potential energy to rotational energy, resulting in less kinetic energy at the bottom.
- 📝 Alan acknowledges a mistake in reading the percentage of the frictional force and corrects the approach to understanding the forces at play.
- 🎓 The video concludes with an offer for free homework help on Twitch or Discord, encouraging viewers to engage for further learning.
Q & A
What is the main topic of the video?
-The main topic of the video is to analyze a free response question from the 2016 AP Physics 1 exam involving a wooden wheel rolling down a ramp with friction.
What is the mass of the wooden wheel discussed in the video?
-The mass of the wooden wheel is denoted as 'M' in the video, but the specific numerical value is not provided.
What are the forces acting on the wooden wheel as it rolls down the ramp?
-The forces acting on the wooden wheel are gravity (mg), static friction, and the normal force from the ramp.
Why is the friction force important in this scenario?
-The friction force is important because it is the only force that can change the angular velocity of the wheel through torque, which is essential for the wheel to rotate.
What is the direction of the friction force acting on the wheel?
-The friction force acts in the direction opposite to the motion of the wheel, resisting its movement down the ramp.
How does the normal force relate to the wheel's motion on the ramp?
-The normal force is perpendicular to the ramp and balances the component of gravity acting in the direction perpendicular to the ramp, preventing the wheel from sinking into the ramp.
What is the relationship between the force of friction and the normal force?
-The force of friction is proportional to the normal force, but in this case, it is 40% of the maximum static friction force, not the full normal force.
What is the approximate linear acceleration of the wheel's center of mass in terms of M, theta, and physical constants?
-The linear acceleration of the wheel's center of mass can be derived from the net force in the X direction, which is mg sine theta minus 0.4 times the normal force, and then equated to mass times acceleration (M * a).
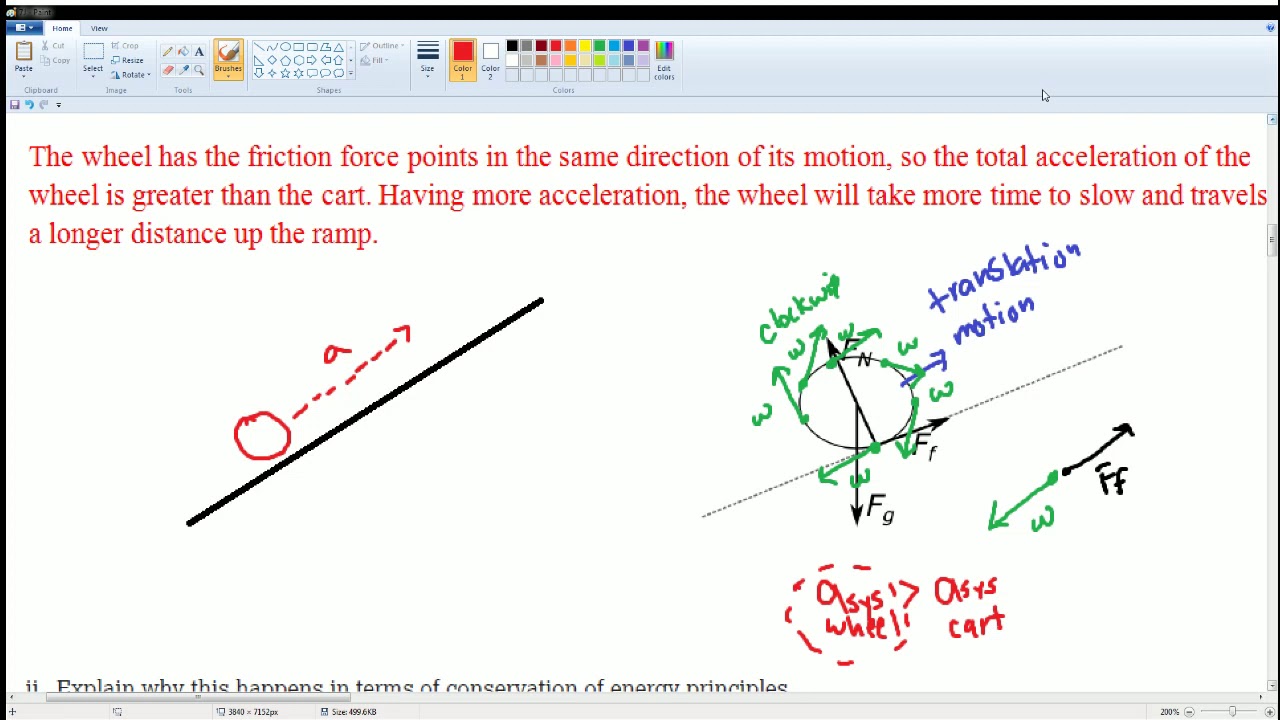
Why does the block of ice reach the bottom of the ramp with a greater speed than the wheel?
-The block of ice reaches the bottom with a greater speed because it only converts potential energy into kinetic energy, whereas the wheel has to use some of the potential energy to cause rotation, leaving less kinetic energy.
What is the significance of the ramp's angle (theta) in the problem?
-The ramp's angle (theta) is significant as it determines the components of the gravitational force acting on the wheel in the X and Y directions, which in turn affects the wheel's acceleration and torque.
What is the error the presenter made in the video regarding the friction force?
-The presenter mistakenly read the friction force as 40% of the normal force instead of correctly interpreting it as 40% of the force component directed opposite to the force of friction, which is mg sine theta.
Why does the presenter suggest that the block of ice would have a larger kinetic energy at the bottom of the ramp?
-The presenter suggests that the block of ice has a larger kinetic energy because it does not have to expend energy on rotation, unlike the wheel, which means all of its potential energy is converted into kinetic energy.
Outlines
📚 AP Physics 1 Free Response Question Analysis
In this segment, Alan from Bothell STEMcoach introduces a free response question from the 2016 AP Physics 1 exam. The question involves a wooden wheel rolling down an inclined ramp with a force of static friction acting on it. Alan explains the forces acting on the wheel, including gravity, friction, and the normal force, and emphasizes the importance of identifying these forces to understand the wheel's motion. He also discusses the concept of torque and how it relates to the wheel's angular acceleration, concluding that only the friction force contributes to the wheel's rotation due to its non-zero torque.
🔍 Calculating Linear Acceleration with Free Body Diagram
Alan proceeds to set up a free body diagram to calculate the linear acceleration of the wheel's center of mass. He breaks down the gravitational force into its components along the ramp and perpendicular to it. The normal force and the frictional force, which is 40% of the maximum static friction, are also considered. By analyzing the forces in the Y and X directions, Alan derives an expression for the linear acceleration 'a' in terms of the mass 'M', the ramp angle 'theta', and other physical constants. He corrects a misreading of the percentage value related to the frictional force and reaffirms the method's validity without the need for torque calculations.
🏁 Comparing Wheel and Block Speeds on an Inclined Ramp
In the final part of the script, Alan discusses an experiment comparing the speeds of a wheel and a block of ice sliding down the same ramp from the same height. He explains that the block, experiencing negligible friction, will reach the bottom with greater speed than the wheel, which has to convert some of its potential energy into rotational energy. Alan clarifies the energy conversion process, stating that the wheel's need to rotate uses up some of the potential energy, leaving it with less kinetic energy at the bottom of the ramp. He admits to misinterpreting the question's phrasing regarding the frictional force but confirms that the block will have a higher speed due to the absence of rotational energy requirements.
Mindmap
Keywords
💡AP Physics
💡Free Response Question
💡Center of Mass
💡Static Friction
💡Normal Force
💡Torque
💡Angular Acceleration
💡Linear Acceleration
💡Potential Energy
💡Kinetic Energy
💡Frictionless
Highlights
Alan introduces an AP Physics 1 free response question from the 2016 exam.
The problem involves a wooden wheel of mass M rolling down a ramp with an angle theta.
Static friction is acting on the wheel, preventing slipping as it rolls.
The task is to label the forces acting on the wheel without breaking them into components.
Gravity, friction, and normal force are the primary forces discussed.
Torque is identified as a key factor in changing the angular velocity of the wheel.
The friction force is the only force causing the wheel to rotate due to its non-zero torque.
An expression for the linear acceleration of the wheel's center of mass is derived using M, theta, and physical constants.
A free body diagram is set up to solve for the acceleration, considering gravity's components and friction.
The frictional force is calculated as 40% of the maximum static friction force.
The normal force is determined to balance the component of gravity acting perpendicular to the ramp.
A block of ice with the same mass M is released from the same height without friction for comparison.
The block reaches the bottom of the ramp with greater speed due to the absence of friction.
The energy conversion from potential to kinetic and rotational energy is explained.
The wheel's rotation requires energy, leaving it with less kinetic energy compared to the block.
Alan admits to a misreading of the percentage of static friction in the problem setup.
The correct reasoning for the block having a greater speed is provided, attributing it to the absence of friction.
Alan offers free homework help on Twitch or Discord for further learning and questions.
Transcripts
Browse More Related Video

2016 #1 Free Response Question - AP Physics 1 - Exam Solution

AP Physics 1 Work and Energy Practice Problems and Solutions

2021 AP Physics 1 Free Response #4 (First Administration)

2017 AP Physics 1 Free Response #2
AP Physics Workbook 7.K Rolling/Sliding/Both
AP Physics Workbook 7.J Translation vs Rotation
5.0 / 5 (0 votes)
Thanks for rating: