AP Physics Workbook 4.D Spring Potential Energy Lab
TLDRIn this AP Physics workbook, students explore the conservation of mechanical energy through an experiment with a spring. The focus is on demonstrating that all mechanical energy initially in the form of elastic potential energy is transformed into other forms, specifically kinetic and gravitational potential energy. The theoretical setup involves Hooke's law and energy conservation equations, with practical steps including measuring mass, compression, and height, and using kinematics to calculate velocity. The experiment's accuracy is enhanced by conducting multiple trials and averaging results, with potential errors discussed. The impact of an incorrect spring constant on the results is also examined, highlighting the importance of precise measurements for accurate outcomes.
Takeaways
- 📚 The experiment aims to demonstrate the conservation of mechanical energy, specifically showing the transformation of energy from elastic potential to other forms of mechanical energy.
- 🌟 The theoretical foundation is based on Hooke's law and the conservation of energy principle, which states that the total mechanical energy (kinetic + potential) remains constant in an isolated system.
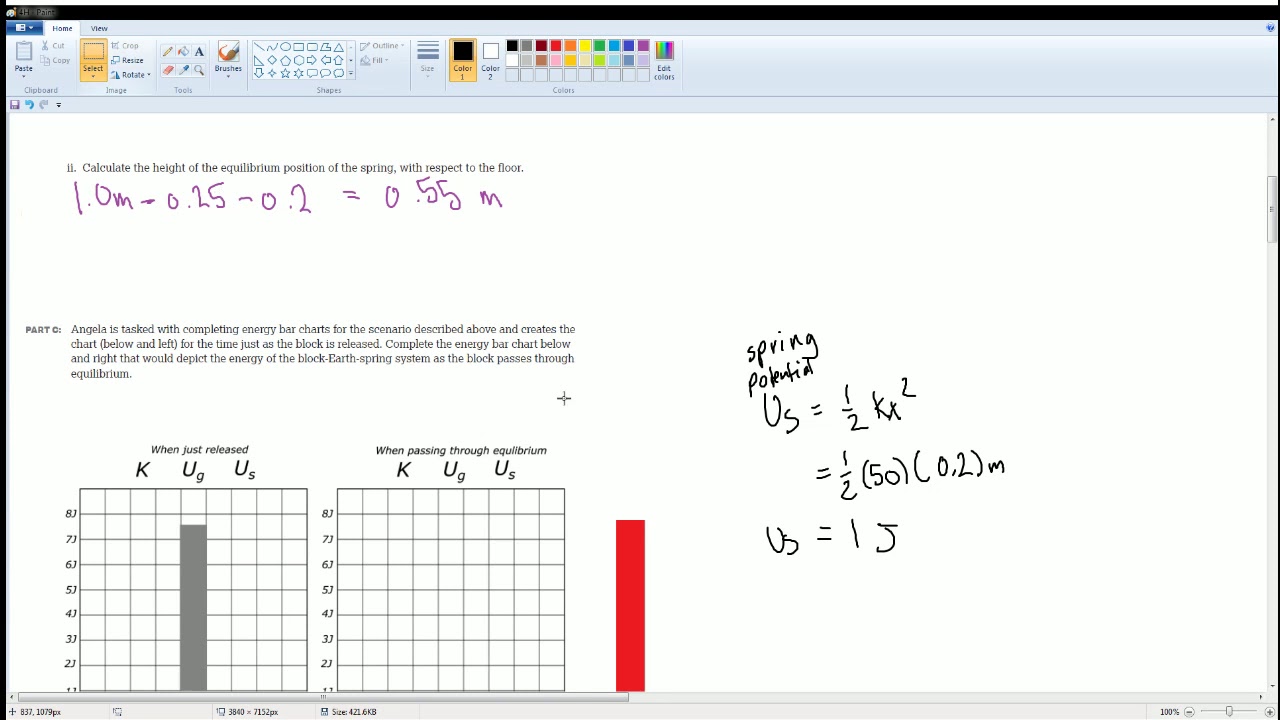
- 📈 The potential energy of a spring is given by the formula 1/2 kx^2, where x is the displacement from the equilibrium position.
- 🔄 The conservation of energy equation is 1/2 kx^2 (spring potential) + mgh (gravitational potential) = 1/2 mv^2 (kinetic energy), which must hold true throughout the experiment.
- 🎢 The experimental setup involves compressing a spring, releasing it, and observing its motion up a ramp to convert elastic potential energy to gravitational potential energy.
- 📏 Key variables to measure include the spring constant (k), the compression distance (x), the mass of the cart (m), and the height (H) achieved by the cart.
- 🔧 The procedure involves marking the equilibrium position, compressing the spring to a known distance, releasing it, and measuring the height at the highest point reached by the cart.
- 🚫 To minimize experimental error, it is suggested to perform the experiment multiple times and average the results, or use precise measuring tools like a meter stick and camera.
- 📊 Data analysis can be done by graphing the spring potential energy versus the gravitational potential energy to verify the linear relationship and conservation of energy.
- 🔄 If the measured spring constant is larger than expected, it would result in a higher gravitational potential energy at the end, indicating a discrepancy in the energy conservation.
- 💡 The experiment can be enhanced by including intermediate steps, such as measuring velocity at the midpoint of the ramp, to provide a more comprehensive understanding of energy transformation.
Q & A
What is the main focus of the AP Physics workbook section discussed in the transcript?
-The main focus is on the conservation of mechanical energy, specifically demonstrating how all the mechanical energy in a system, initially in the form of elastic potential energy, is transformed into another form of mechanical energy.
What is the formula for the potential energy of an elastic spring?
-The potential energy of an elastic spring is given by the formula PE = (1/2)kx^2, where x is the distance the spring is compressed or stretched from its equilibrium position.
According to Hooke's law, what happens to the spring when it is released after being compressed or stretched?
-When the spring is released after being compressed or stretched, it exerts a restorative force and returns to its original shape, converting the potential energy into kinetic energy.
What are the two forms of mechanical energy mentioned in the script that can be converted into each other?
-The two forms of mechanical energy mentioned are elastic potential energy and kinetic energy (or gravitational potential energy when the object is on a ramp).
How can the conservation of energy principle be applied to the spring system?
-The conservation of energy principle states that the total mechanical energy in the system (sum of kinetic and potential energies) remains constant, ignoring external forces. It can be applied to the spring system by comparing the initial potential energy to the final potential or kinetic energy to show that they are equal.
What is the procedure for setting up the experiment to demonstrate the conservation of mechanical energy?
-The procedure involves placing the cart at the equilibrium position, compressing the spring and marking the distance (X), releasing the cart, and observing its motion. If a motion gate is available, the velocity at the midpoint can be measured. The final step is to measure the height (H) the cart reaches at the top of the ramp using trigonometry.
How can experimental errors be reduced in the described experiment?
-Errors can be reduced by conducting multiple trials (at least ten) and averaging the results, such as the height reached by the cart at the top of the ramp, to account for any overshoots or undershoots.
What would be the effect on the experiment's results if the spring constant (k) were larger than initially measured?
-If the spring constant (k) were larger, the spring's potential energy would be greater, resulting in a higher gravitational potential energy at the end of the experiment, as the cart would reach a higher point on the ramp than expected.
How can the data from the experiment be used to verify the correctness of the results?
-The data can be graphed, plotting spring potential energy against gravitational potential energy. A linear relationship should be observed, with the line of best fit showing the conversion of the spring's potential energy into the ramp's potential energy.
What is the significance of measuring the height at the highest point the object reaches?
-Measuring the height at the highest point is crucial because it represents the gravitational potential energy of the object at that point. This measurement is used to verify the conservation of energy by comparing it to the initial spring potential energy.
How does the mass of the cart (object) affect the conservation of mechanical energy demonstration?
-The mass of the cart affects the kinetic and gravitational potential energies in the system. A more massive cart will have greater kinetic energy when released and will reach a higher point on the ramp, converting more potential energy into kinetic energy and vice versa.
What is the role of trigonometry in this experiment?
-Trigonometry is used to calculate the height (H) the cart reaches at the top of the ramp, which is essential for determining the gravitational potential energy and verifying the conservation of mechanical energy principle.
Outlines
📚 Introduction to AP Physics Workbook - Mechanical Energy Conservation
This paragraph introduces the viewer to the AP Physics workbook focusing on the concept of work and energy, specifically point D spring potential energy. The scenario involves students who have already determined the spring constants through an experiment and are now tasked with demonstrating the conservation of mechanical energy. The goal is to show that all the mechanical energy in a system, initially in the form of elastic potential energy, is transformed into another form of mechanical energy. The theoretical background is explained, including the potential energy of an elastic spring, Hooke's law, and the conservation of mechanical energy principle. The paragraph sets the stage for the experiment by discussing the theoretical setup and the expected energy transformations.
🧪 Lab Procedure and Setup - Measuring Mechanical Energy Conservation
This paragraph delves into the lab procedure and setup for demonstrating the conservation of mechanical energy. It outlines the steps for conducting the experiment, starting with measuring the spring's compression distance (X) from its equilibrium position. The paragraph discusses the importance of marking the equilibrium position and the potential for gravitational potential energy at the start. It also mentions the use of a motion gate to measure the object's velocity and the final step of the object reaching the top of the ramp, where trigonometry is used to calculate the height. The paragraph emphasizes the need to understand the theoretical setup and the equations governing the calculation of mass, compression distance, and final height. Additionally, it suggests methods to reduce experimental error, such as conducting multiple experiments and averaging the results.
📈 Data Analysis and Error Reduction - Mechanical Energy Conservation
The final paragraph focuses on data analysis and methods to reduce experimental error in the context of mechanical energy conservation. It explains how to graph the spring potential energy versus the gravitational potential energy to demonstrate the linear relationship between the two. The paragraph also discusses the optional step of graphing the middle step of the experiment, which involves calculating the kinetic energy at the midpoint. It addresses the potential impact of an incorrect spring constant measurement on the results, explaining how a larger spring constant would result in a higher gravitational energy at the end of the experiment. The paragraph concludes by reiterating the importance of understanding the conservation of energy principle and provides a summary of the key points and notes discussed in the video script.
Mindmap
Keywords
💡Conservation of Mechanical Energy
💡Elastic Potential Energy
💡Spring Constant
💡Gravitational Potential Energy
💡Kinetic Energy
💡Experimental Error
💡Procedure
💡Spring Displacement
💡Height Measurement
💡Graphing Data
Highlights
The main focus of the transcript is an experiment to demonstrate the conservation of mechanical energy using a spring and a ramp.
The spring's potential energy is given by the formula 1/2 kx^2, where x is the distance from its equilibrium position.
The conservation of mechanical energy is based on the principle that total mechanical energy (kinetic + potential) remains constant in an isolated system.
The experiment involves compressing the spring, releasing it, and observing the conversion of elastic potential energy to other forms of mechanical energy.
At the start of the experiment, all the mechanical energy is in the form of potential energy stored in the compressed spring.
Upon release, the spring's potential energy is transformed into kinetic energy as the object moves.
The conservation of energy equation for the system is 1/2 kx^2 (spring potential) + 1/2 mgh (gravitational potential) = 1/2 mv^2 (kinetic energy).
The experiment requires measuring the spring constant (k), the mass (m), the compression distance (x), and the final height (H).
To reduce experimental error, the procedure suggests compressing the same mass with different spring displacements and averaging the results.
The height reached by the object at the end of the experiment can be determined using trigonometry.
Graphing the spring potential energy versus the gravitational potential energy can help verify the conservation of energy principle.
If the spring constant is larger than initially measured, the gravitational potential energy at the end will be greater, indicating a higher point on the ramp.
A lower spring constant would result in a lower point on the ramp, suggesting less energy conversion.
The procedure involves marking the equilibrium position, compressing the spring, releasing it, and recording the height reached by the object.
Using a motion gate or a stopwatch can help measure the time it takes for the object to pass the midpoint of the ramp.
The theoretical setup is crucial for understanding the experiment's design and expected outcomes.
The experiment provides a practical application of Hooke's law and the conservation of mechanical energy principles.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: