Gravitational and Elastic Potential Energy

The Physics Classroom
24 Sept 202110:50
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial delves into the concept of potential energy, focusing on gravitational and elastic potential energy. It explains how gravitational potential energy is calculated using mass, height, and gravitational field strength, and how it varies with height. The tutorial also covers the zero level's significance in measuring height and potential energy. Elastic potential energy is introduced through Hooke's Law and the equation relating spring force to stretch, highlighting its direct proportionality to the square of the stretch. The video concludes with an action plan for further learning and resources available on the website.

Takeaways
  • πŸ“š Potential energy is the energy stored in an object due to its position, with two main types discussed: gravitational and elastic potential energy.
  • 🌐 Gravitational potential energy (GPE) is calculated using the formula PE = m * g * h, where m is mass, g is the gravitational field strength (approximately 9.8 N/kg on Earth), and h is height above a reference point.
  • πŸ“ˆ The value of GPE increases with the mass of the object and its height above the reference point, and is measured in joules (J), the same unit for work.
  • πŸ”„ The concept of zero height or reference level is arbitrary and can be chosen based on convenience for calculations.
  • πŸ“‰ As height increases, GPE increases, and as height decreases, GPE decreases, with the potential energy being greatest at the highest point and least at the lowest point in an object's motion.
  • πŸ€” The formula for GPE can be rearranged to solve for any of the variables (PE, m, h) if the other two are known, providing a method to calculate mass or height given the other values.
  • 🏹 Elastic potential energy is associated with the deformation of a spring, which stores energy when stretched or compressed.
  • πŸ”— Hooke's Law describes the relationship between the force applied to a spring and the amount of stretch, expressed as F = k * Ξ”x, where k is the spring constant and Ξ”x is the displacement.
  • πŸ”„ The elastic potential energy stored in a spring is given by the formula PE_elastic = 1/2 * k * Ξ”x^2, where Ξ”x is the displacement from the spring's equilibrium position.
  • πŸ‘ The potential energy stored in a spring is always positive, regardless of whether the spring is stretched or compressed.
  • πŸ“ˆ The spring constant (k) is a measure of the stiffness of the spring, with higher values indicating stiffer springs and lower values indicating softer springs.
Q & A

  • What is potential energy?

    -Potential energy is the energy stored in an object due to its position relative to other objects or forces, such as the Earth's gravitational field or the tension in a spring.

  • What are the two main types of potential energy discussed in the video?

    -The two main types of potential energy discussed are gravitational potential energy and elastic potential energy.

  • How is gravitational potential energy calculated?

    -Gravitational potential energy (PE) is calculated using the formula PE = m * g * h, where m is the mass of the object in kilograms, g is the gravitational field strength (approximately 9.8 N/kg on Earth), and h is the height of the object in meters above a reference point.

  • What is the standard unit of energy, and how does it relate to the units in the gravitational potential energy formula?

    -The standard unit of energy is the joule (J). In the context of gravitational potential energy, one joule is equivalent to the product of a newton-meter, which arises from the units of mass (kg), gravitational acceleration (N/kg), and height (m).

  • How does the height of an object affect its gravitational potential energy?

    -The gravitational potential energy of an object increases with the height of the object. As the object is raised higher, more work is done against gravity, resulting in more potential energy stored in the object.

  • What is an arbitrary zero level, and why is it important in calculating potential energy?

    -An arbitrary zero level is a reference point chosen for convenience when calculating potential energy. It is important because the potential energy of an object is relative to this reference point, and different choices of zero level can result in different numerical values for the same object's potential energy.

  • What is Hooke's Law, and how does it relate to elastic potential energy?

    -Hooke's Law states that the force (F) exerted by a spring is directly proportional to the displacement (delta x) from its equilibrium position, expressed as F = k * delta x, where k is the spring constant. This law is fundamental to understanding how elastic potential energy is stored in a spring, as the more the spring is stretched or compressed, the more potential energy is stored.

  • How is elastic potential energy in a spring calculated?

    -Elastic potential energy stored in a spring is calculated using the formula PE = 0.5 * k * delta x^2, where k is the spring constant and delta x is the displacement from the spring's equilibrium position.

  • Why is the potential energy always positive, regardless of whether the spring is stretched or compressed?

    -Potential energy is always positive because it represents the stored energy in the system. The formula for elastic potential energy (PE = 0.5 * k * delta x^2) includes the square of the displacement, which ensures that the value is always positive, regardless of the direction of the displacement (stretching or compressing).

  • What is the significance of the spring constant (k) in the context of elastic potential energy?

    -The spring constant (k) is a measure of the stiffness of the spring. It determines the amount of force needed to stretch or compress the spring by a given distance. A larger spring constant indicates a stiffer spring that stores more elastic potential energy for the same amount of displacement.

  • How can the equations for gravitational and elastic potential energy be used to solve for unknown variables?

    -The equations can be rearranged to solve for any of the variables if the other two are known. For example, to find the mass (m) in gravitational potential energy, you would rearrange the equation to m = PE / (g * h). Similarly, for elastic potential energy, to find the spring constant (k), you could rearrange the equation to k = 2 * PE / (delta x^2).

Outlines
00:00
πŸ“š Introduction to Potential Energy and Gravitational Potential Energy

This paragraph introduces the concept of potential energy as the energy stored in an object due to its position. It focuses on two types of potential energy: gravitational and elastic. Gravitational potential energy is explained with the example of a wrecking ball raised high above the ground, while elastic potential energy is illustrated with a stretched bowstring. The paragraph explains that gravitational potential energy depends on the mass of the object and its height above a reference point, and it is calculated using the formula PE = m*g*h, where m is mass, g is the acceleration due to gravity, and h is height. The importance of choosing a reference level for zero potential energy is also discussed, with examples of how different choices can affect the calculated potential energy.

05:00
πŸ“ˆ Calculation of Gravitational Potential Energy and the Concept of Zero Level

This paragraph delves deeper into the calculation of gravitational potential energy, emphasizing the significance of the zero level or reference height from which potential energy is measured. It provides a practical example using a staircase diagram with balls of mass one kilogram placed at different heights. The potential energy of each ball is calculated based on three different arbitrary zero levels, demonstrating how the choice of zero level affects the calculated values. The paragraph also explains how to rearrange the gravitational potential energy formula to solve for mass or height when the other variables are known, highlighting the equation's utility in various physics problems.

10:02
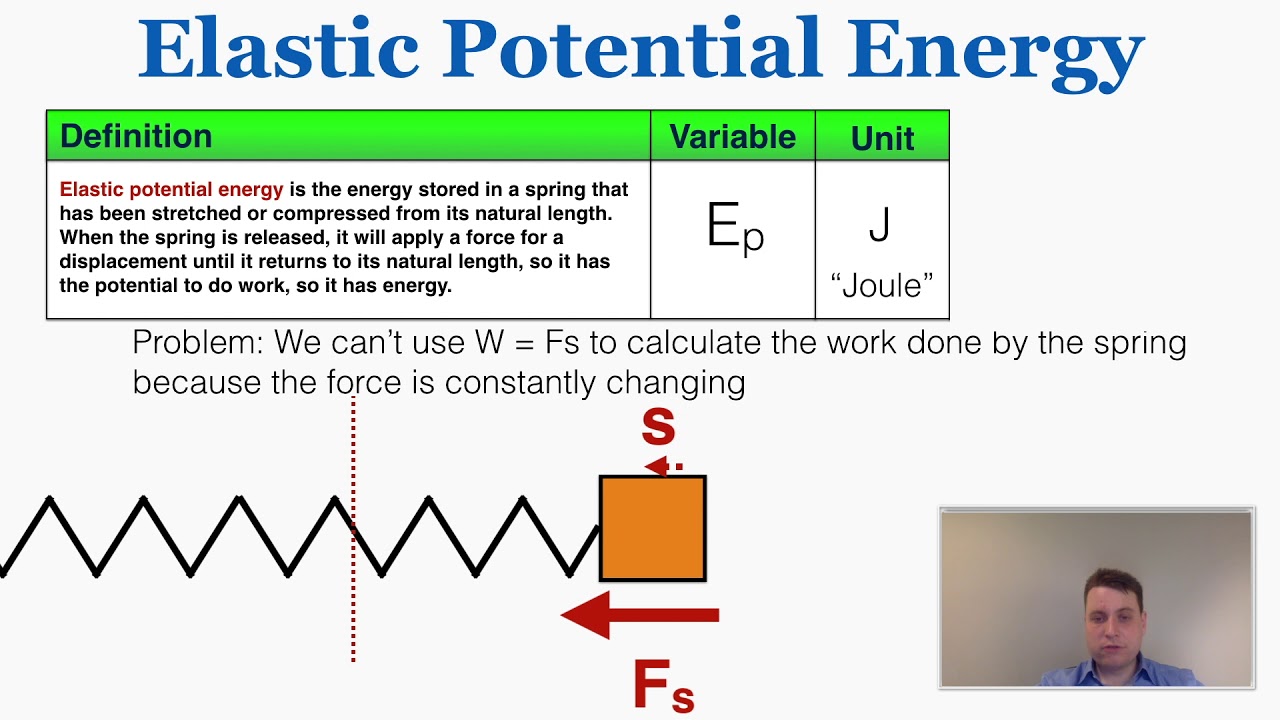
πŸ” Hooke's Law and Elastic Potential Energy in Springs

The final paragraph shifts the focus to elastic potential energy, starting with an exploration of Hooke's Law, which describes the linear relationship between the force applied to a spring and the amount of stretch or compression it undergoes. The spring constant, a measure of the spring's stiffness, is introduced, and its role in Hooke's Law is explained. The paragraph then connects the concept of spring force to elastic potential energy, explaining that the energy stored in a spring is proportional to the square of its stretch or compression, as given by the formula for elastic potential energy, which is PE = 1/2 * k * (Ξ”x)^2, where k is the spring constant and Ξ”x is the displacement from the spring's equilibrium position. The paragraph concludes with an action plan for further learning and an invitation for viewer engagement.

Mindmap
Keywords
πŸ’‘Potential Energy
Potential energy is the stored energy in an object due to its position relative to other objects. In the context of the video, it is the energy stored in an object as a result of its position within a gravitational field or due to its elastic deformation. The script discusses two types of potential energy: gravitational and elastic, and how they are calculated, emphasizing the role of potential energy in physics.
πŸ’‘Gravitational Potential Energy
Gravitational potential energy is a form of potential energy that an object possesses due to its elevated position in a gravitational field. The video explains that it depends on the object's mass and height above a reference point. The formula for calculating gravitational potential energy is given as PE = m*g*h, where m is mass, g is the acceleration due to gravity, and h is height.
πŸ’‘Elastic Potential Energy
Elastic potential energy is the energy stored in an elastic object, such as a spring, when it is stretched or compressed. The video illustrates this concept with the example of a bowstring being stretched. It is related to the spring force and is calculated using the formula PE = 1/2 * k * delta_x^2, where k is the spring constant and delta_x is the displacement from the equilibrium position.
πŸ’‘Mass
Mass is a measure of the amount of matter in an object, typically measured in kilograms. In the video, mass (m) is a key variable in the formula for gravitational potential energy, indicating that the greater the mass of an object, the more potential energy it has when raised to a certain height.
πŸ’‘Height
Height is the vertical distance of an object above a reference level. In the context of gravitational potential energy, the video explains that height (h) is a crucial factor in determining the amount of potential energy an object possesses. The higher the object is lifted, the more work is done on it, and the greater its potential energy.
πŸ’‘Spring Constant
The spring constant (k) is a measure of a spring's stiffness and is used in Hooke's Law to calculate the force needed to stretch or compress a spring. The video mentions that it has units of newtons per meter and is directly related to the amount of elastic potential energy stored in a spring.
πŸ’‘Hooke's Law
Hooke's Law is a principle that describes the linear relationship between the force applied to a spring and the displacement of the spring from its equilibrium position. The video uses this law to explain the direct proportionality between the force applied to a spring and the amount of stretch, which is expressed as F = k * delta_x.
πŸ’‘Displacement
Displacement (delta_x) refers to the change in position of an object, in this case, the stretch or compression of a spring from its equilibrium position. The video explains that the elastic potential energy stored in a spring is directly related to the square of this displacement, as shown in the formula for elastic potential energy.
πŸ’‘Joule
The joule (J) is the standard unit of energy in the International System of Units (SI). The video mentions that the unit of potential energy is a newton-meter, which is equivalent to a joule, indicating that energy and work share the same units.
πŸ’‘Zero Level
Zero level is an arbitrary reference point used to measure the height or position of an object. The video explains the importance of choosing a convenient zero level when calculating gravitational potential energy, as it affects the calculated values of potential energy for objects at different heights.
πŸ’‘Work
Work is the energy transferred to or from an object via the application of force along a displacement. In the video, work is described as being done on an object when it is lifted against gravity, which results in the storage of gravitational potential energy.
Highlights

Introduction to potential energy as energy stored in an object due to its position.

Discussion on two types of potential energy: gravitational and elastic potential energy.

Explanation of gravitational potential energy in relation to an object's position in Earth's gravitational field.

Elastic potential energy is explained through the example of a stretched bowstring.

Gravitational potential energy formula: PE = m * g * h.

The standard unit of energy is the joule, and its relation to the formula for gravitational potential energy.

The impact of height on gravitational potential energy and its calculation.

The concept of zero height as an arbitrary decision for calculating potential energy.

Illustration of calculating potential energy with different zero levels using a staircase diagram.

The ability to calculate any of the three variables (PE, m, h) in the gravitational potential energy equation.

Introduction to Hooke's Law and its relation to spring force and elastic potential energy.

Elastic potential energy formula: Elastic PE = 1/2 * k * delta x^2.

The significance of the spring constant (k) in determining the stiffness of a spring.

Action plan for further learning and resources provided by the video creator.

Invitation for audience engagement through likes, subscriptions, and comments.

Transcripts

Browse More Related Video

College Physics 1: Lecture 29 - Forms of Energy

Gravitational Potential and Gravitational Potential Energy

Elastic Potential Energy - IB Physics

AP Physics Workbook 4.D Spring Potential Energy Lab

(previous version) Introduction to Elastic Potential Energy with Examples

Potential Energy | Science for Kids

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Potential EnergyGravitationalElasticPhysicsTutorialWorkEnergySpring ForceHooke's LawMr HEducational