AP Physics Workbook 1.J Vertrical Motion
TLDRThe video script discusses a physics problem involving a rocket's vertical motion. It explains the rocket's constant upward acceleration of 5 m/s^2 for the first 10 seconds, followed by freefall due to gravity after the engine shuts off. The script guides through drawing acceleration, velocity, and displacement graphs, and calculating the rocket's final velocity and height. It concludes with explaining the rocket's deceleration to 9.8 m/s^2 downwards at 10.1 seconds and clarifies that the rocket is still moving upwards despite the net force being downwards.
Takeaways
- 🚀 The rocket undergoes vertical motion with an initial upward acceleration of 5 m/s².
- ⏱️ The constant acceleration lasts for the first 10 seconds of the rocket's launch.
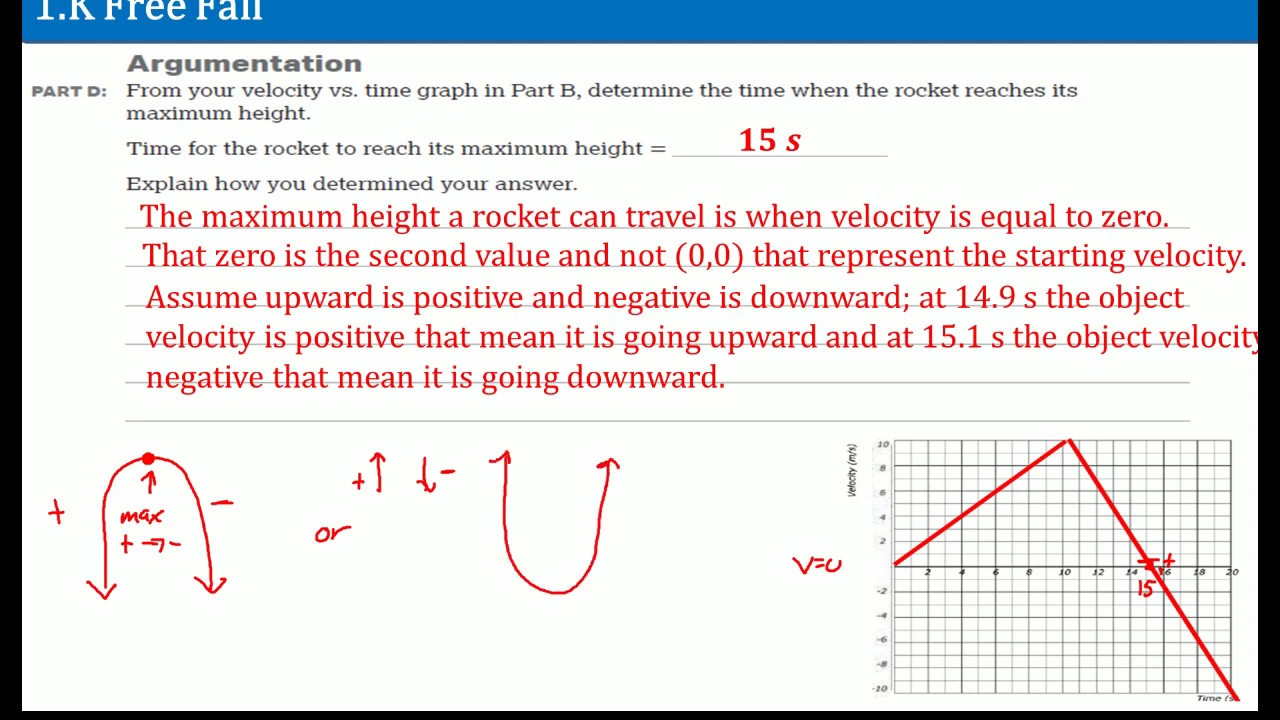
- 📈 The acceleration graph for the first 10 seconds is a straight line starting at 5 m/s and rising to 50 m/s.
- 🛫 After 10 seconds, the rocket's engine shuts off, leading to free fall with acceleration due to gravity.
- 🌌 The deceleration at 10.1 seconds after launch is 9.8 m/s² downwards due to gravity.
- 📊 The velocity-time graph shows a positive slope during the first 10 seconds, indicating constant upward velocity.
- 📈 The displacement graph is a triangle with a base of 10 seconds and a height of 50 m/s, yielding an area of 250 m.
- 🔢 The height reached by the rocket can be calculated using the area under the velocity-time graph for the first 10 seconds.
- 🌐 At 10.1 seconds, despite the change in acceleration, the rocket is still moving upwards due to its initial velocity.
- 💫 The rocket's motion after the engine shuts off involves a gradual deceleration followed by a downward curving path due to gravity.
- 📚 Understanding the relationship between velocity, acceleration, and time is crucial for solving problems involving motion.
Q & A
What is the initial acceleration of the rocket as described in the transcript?
-The initial acceleration of the rocket is 5 meters per second squared, acting upwards.
For how long does the rocket continue to accelerate upwards?
-The rocket continues to accelerate upwards for 10 seconds.
What happens to the rocket's acceleration after the engine shuts off at 10 seconds?
-After the engine shuts off at 10 seconds, the rocket experiences free fall, with an acceleration equal to the gravitational acceleration, which is approximately 9.8 meters per second squared acting downwards.
How does the rocket's velocity change during the 10 seconds of upward acceleration?
-The rocket's velocity increases linearly from zero to 50 meters per second during the 10 seconds of upward acceleration, given the constant acceleration of 5 meters per second squared.
What is the height reached by the rocket at the end of the 10 seconds of upward acceleration?
-The height reached by the rocket at the end of the 10 seconds is 250 meters, calculated using the area under the velocity-time graph as half the product of the base (time) and height (final velocity).
What is the direction of the rocket's acceleration at 10.1 seconds after launch?
-At 10.1 seconds after launch, the direction of the rocket's acceleration is downwards, due to the force of gravity.
Is the rocket still moving upwards at 10.1 seconds after launch?
-Yes, the rocket is still moving upwards at 10.1 seconds after launch, although it is starting to decelerate due to the gravitational force acting on it.
How does the shape of the velocity-time graph reflect the rocket's motion?
-The shape of the velocity-time graph is a straight line with a positive slope, reflecting the constant upward acceleration. The line ends at a velocity of 50 m/s, indicating the rocket's velocity at the end of the 10 seconds of acceleration.
What is the significance of the area under the velocity-time graph in determining the height reached by the rocket?
-The area under the velocity-time graph represents the displacement of the rocket, which in this case is the height it reaches during the upward acceleration phase.
How does the absence of the engine's thrust after 10 seconds affect the rocket's motion?
-After the engine's thrust is shut off, the rocket no longer has an upward force to counteract gravity. As a result, it begins to decelerate due to the gravitational force acting downwards, and eventually, it will start to move back towards the Earth.
What is the expected motion of the rocket after it reaches its maximum height?
-After reaching its maximum height, the rocket will start to move downwards due to the force of gravity, following a parabolic trajectory if air resistance is neglected.
Outlines
🚀 Rocket Launch and Vertical Motion
This paragraph introduces the scenario of a rocket's vertical motion, detailing its launch with an upward acceleration of 5 m/s^2 for 10 seconds. It emphasizes the importance of understanding the constant acceleration during this period and how to represent it graphically. The speaker attempts to sketch a graph of acceleration versus time, explaining the significance of the slope in the graph. The paragraph concludes with a discussion on how to calculate the rocket's velocity after 10 seconds using the graph and the constant acceleration value.
📈 Determining Height from Velocity Graph
The second paragraph focuses on converting the rocket's velocity information into height. It explains the process of calculating the area under the velocity-time graph to determine the height reached by the rocket. The speaker clarifies the shape of the graph as a triangle and uses the formula for the area of a triangle to calculate the height. Additionally, the paragraph addresses the change in acceleration after 10.1 seconds, explaining the transition from positive acceleration to the gravitational acceleration acting downwards, and how this affects the rocket's motion.
🔢 Analysis of Rocket's Deceleration and Direction
In the final paragraph, the speaker analyzes the rocket's deceleration after the engine shuts off at 10.1 seconds. It explains the change in acceleration to 9.8 m/s^2 downwards due to gravity and how this causes the rocket to start falling back to the surface. The speaker corrects a previous mistake and confirms that the rocket is still moving upwards at 10.1 seconds, despite the net force now being directed downwards. The paragraph concludes with a summary of the solution for the given problem, providing a clear understanding of the rocket's motion and the forces acting upon it.
Mindmap
Keywords
💡Vertical Motion
💡Acceleration
💡Rocket
💡Freefall
💡Velocity
💡Force
💡Graph
💡Displacement
💡Time
💡Height
💡Deceleration
Highlights
The transcript discusses a physics problem involving vertical motion, specifically the launch of a rocket.
The rocket is launched straight up with an initial acceleration of 5 m/s^2.
The engine operates for the first 10 seconds of the rocket's flight.
After 10 seconds, the engine shuts off, and the rocket begins to fall back to the surface under the influence of gravity.
The problem requires sketching a graph of acceleration as a function of time from T=0 to T=10 seconds.
The acceleration graph is a straight horizontal line at 5 m/s^2 for the first 10 seconds, representing constant acceleration.
The velocity graph of the rocket is also required, which is a positively sloped line due to the constant upward acceleration.
The velocity of the rocket at the end of 10 seconds is calculated to be 50 m/s.
The height reached by the rocket can be determined by calculating the area under the velocity-time curve.
The area under the curve, representing the height, is calculated to be 250 meters using the formula for the area of a triangle.
At 10.1 seconds after launch, the rocket's acceleration is due to gravity and is 9.8 m/s^2 directed downwards.
Despite the change in acceleration to a downward value, the rocket is still moving upwards at 10.1 seconds due to its initial upward velocity.
The explanation involves understanding the transition from upward motion powered by the engine to the freefall motion under gravity.
The problem illustrates fundamental concepts of classical mechanics, such as constant acceleration, velocity, and freefall.
The solution process demonstrates the application of mathematical concepts like graphing and calculating areas to solve physics problems.
The transcript provides a step-by-step walkthrough of the problem, including the use of diagrams and calculations.
The problem and its solution serve as an example of how physics principles can be applied to real-world scenarios like rocket launches.
The transcript's detailed explanation helps to clarify the relationship between force, acceleration, and motion in a vertical context.
The solution highlights the importance of correctly interpreting and applying physical laws to accurately predict the motion of objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: