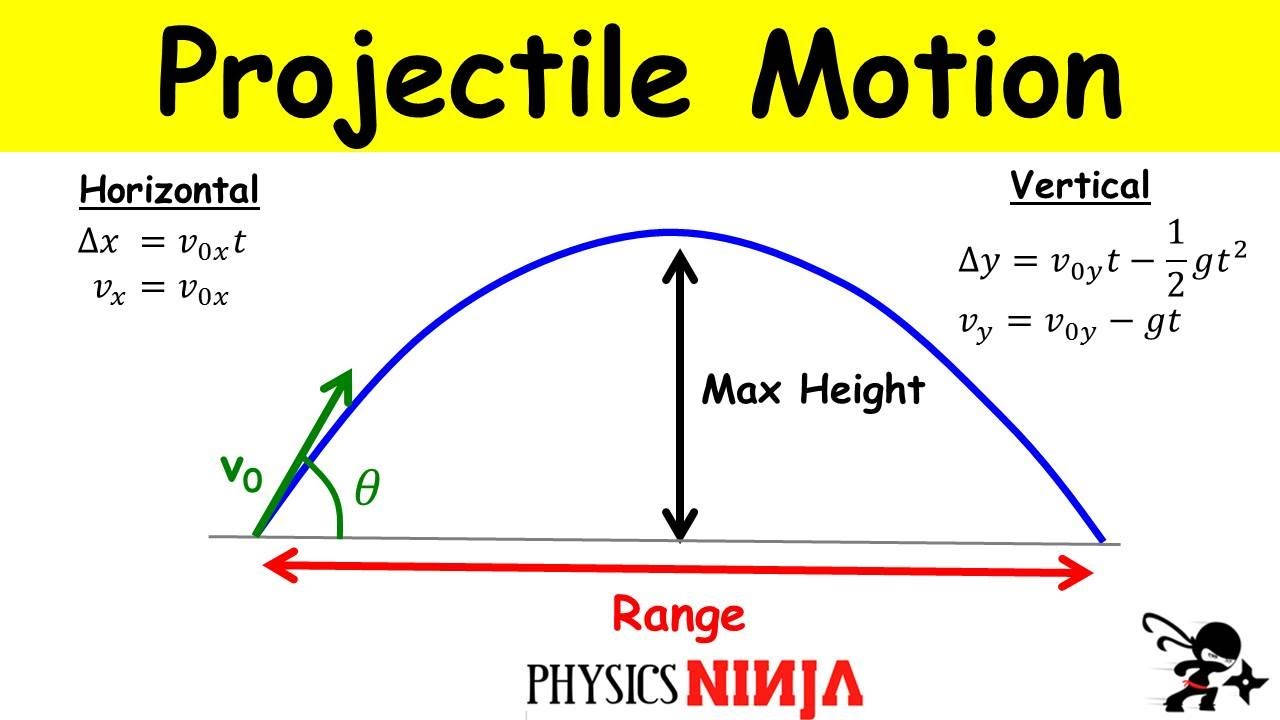
AP Physics Workbook 1.K Free Fall
TLDRThe video script discusses a physics problem involving a rocket that launches vertically with an upward deceleration, then turns around and freefalls back to Earth. It clarifies misconceptions about the kinematics equations used to determine the rocket's landing time and maximum height. The key points include understanding constant acceleration, velocity graphs, and the significance of velocity sign change in relation to maximum height. The script emphasizes the importance of correctly interpreting the physics concepts and equations to solve problems related to freefall and motion.
Takeaways
- 🚀 The scenario involves a rocket launched vertically upwards with an initial deceleration of 5 m/s².
- 🔄 After 10 seconds, the rocket's engine shuts off and it begins to freely fall back to Earth with an acceleration of -9.8 m/s².
- 📈 The velocity graph is linear with a positive slope during the first 10 seconds and a negative slope during the free fall.
- 🌟 The maximum height of the rocket is reached when the velocity becomes zero, indicating a change from upward to downward motion.
- ⏱️ The time at which the rocket reaches its maximum height is 15.1 seconds, identified by the sign change in velocity.
- 📊 The graph of velocity vs. time is used to determine the rocket's motion, showing both ascent and descent phases.
- 🛑 A common mistake is using incorrect acceleration values when solving for the rocket's landing time or maximum height.
- 📐 The maximum height is calculated by determining the area under the velocity-time graph from the start to the maximum height point.
- 🎯 Understanding the kinematics equations and the rocket's acceleration changes are crucial for accurately predicting its motion.
- 🌐 The problem-solving approach should consider the rocket's motion as a paraabolic trajectory with distinct phases of ascent and descent.
- 🔢 The numerical value of the rocket's maximum height requires integration of the velocity function over time to find the area under the curve.
Q & A
What is the initial condition of the rocket in the physics problem?
-The rocket starts from rest, with an initial velocity of zero meters per second.
What is the upward deceleration of the rocket during the first 10 seconds?
-The rocket has an upward deceleration of 5 meters per second squared during the first 10 seconds.
How does the acceleration change when the rocket's engine shuts off after 10 seconds?
-After the engine shuts off, the rocket experiences a constant acceleration due to gravity, which is -9.8 meters per second squared, directed downwards.
What is the significance of the velocity graph in understanding the rocket's motion?
-The velocity graph helps to visualize the rocket's speed at different times, showing whether it is accelerating or decelerating, and when it changes direction.
At what point does the rocket reach its maximum height?
-The rocket reaches its maximum height when the velocity becomes zero, marking the transition from upward motion to downward motion.
How can the maximum height achieved by the rocket be calculated?
-The maximum height can be calculated by determining the area under the velocity-time graph from the start to the time when the velocity is zero, representing the upward journey to the maximum height.
Why is the equation of motion described as a parabola in this scenario?
-The equation of motion is described as a parabola because the rocket's motion is symmetrical, starting from rest, decelerating upwards, reaching a maximum height, and then accelerating downwards due to gravity.
What is the mistake made by the student in the provided solution?
-The student incorrectly used a value of 5 minutes per second squared instead of the correct acceleration due to gravity, -9.8 meters per second squared, for the falling part of the motion.
How does the change in the sign of velocity indicate the maximum height of the rocket?
-The change in the sign of velocity from positive to negative indicates the moment when the rocket changes direction from ascending to descending, which is the point of maximum height.
What is the importance of understanding free fall in physics?
-Understanding free fall is important as it provides insights into the motion of objects under the sole influence of gravity, which is a fundamental concept in physics and has practical applications in various fields such as engineering and astronomy.
Outlines
🚀 Rocket Launch and Free Fall Analysis
This paragraph discusses a physics problem involving a rocket that launches straight up from rest with an upward deceleration of 5 m/s^2 for 10 seconds. The rocket then shuts off its engine and falls back to Earth. The scenario is labeled and explained, with the initial acceleration being positive and constant at 5 m/s^2, and the subsequent acceleration due to gravity being negative at -9.8 m/s^2. The paragraph emphasizes understanding the constant nature of these accelerations and how they result in linear velocity-time graphs. The student's incorrect solution is critiqued, highlighting the misuse of acceleration values and the correct approach to finding the time when the rocket lands on Earth using kinematics equations.
📈 Determining Maximum Height in Free Fall
The second paragraph focuses on analyzing the velocity versus time graph to determine when the rocket reaches its maximum height. It explains that the maximum height is achieved when the velocity equals zero, which occurs at 15 seconds. The explanation clarifies why the zero velocity at 15 seconds is significant, contrasting it with the initial zero velocity when the rocket was at rest. The paragraph also discusses the concept of a parabola in relation to the rocket's trajectory and how the change in the sign of velocity indicates the maximum height. Lastly, it addresses the misconception about the numerical value of the rocket's maximum height, explaining that the area under the velocity-time graph represents the distance traveled upwards to the maximum height, which is the actual height of the rocket.
Mindmap
Keywords
💡Free Fall
💡Acceleration
💡Velocity
💡Deceleration
💡Kinematics Equation
💡Maximum Height
💡Parabola
💡Area Under the Curve
💡Zero Velocity
💡Time of Flight
Highlights
The scenario involves a rocket launching straight up with an upward deceleration of 5 m/s^2 for 10 seconds.
After 10 seconds, the rocket's engine shuts off and it begins to freely fall back to Earth.
During the ascent, the rocket's acceleration is constant at 5 m/s^2, and during the descent, it's constant at -9.8 m/s^2 (due to gravity).
The velocity-time graph for the rocket's motion is linear with a positive slope during ascent and a negative slope during descent.
The maximum height of the rocket is reached when the velocity becomes zero, indicating a change from upward motion to downward motion.
The time at which the rocket reaches its maximum height is 15.1 seconds, as this is when the velocity changes from positive to negative.
The rocket's maximum height cannot be determined solely by the time it takes to reach that height, but rather by analyzing the area under the velocity-time graph.
The area under the velocity-time graph from the start to the maximum height represents the total distance traveled upwards.
Understanding free fall is crucial for determining the time it takes for an object to reach its maximum height and the value of that height.
The motion graph illustrates that the rocket's motion can be described by a parabolic trajectory, starting from rest and ending at rest.
The student's solution is incorrect because they used a value of 5 minutes per second squared instead of the correct -9.8 m/s^2 for the acceleration during the descent.
The velocity graph's shape and the change in the sign of velocity are key indicators of the rocket's maximum height and the point of turning.
The rocket's motion is a practical example of the kinematic equations in action, demonstrating the relationship between acceleration, velocity, position, and time.
The problem-solving approach requires a clear understanding of the kinematics equations and the ability to apply them correctly to the given scenario.
The rocket's motion is a simplified model that helps in understanding the principles of physics, particularly in the context of free fall and Newton's laws of motion.
The analysis of the rocket's motion provides insights into the practical applications of physics in real-world scenarios such as space travel and engineering.
The transcript serves as an educational resource for learning about the physics of motion, particularly the concepts of free fall and the parabolic trajectory of objects.
The detailed explanation of the rocket's motion and the analysis of the velocity graph help in developing a deeper understanding of the fundamental principles of physics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: