Precalculus Final Exam Review
TLDRThis video transcript serves as a comprehensive study guide for pre-calculus students, particularly those preparing for their final exams. It covers a range of topics including exponential equations, inverse functions, logarithmic expressions, piecewise functions, and more. The instructor provides detailed walkthroughs for solving problems and encourages viewers to pause and attempt problems independently before checking the solutions. The video also touches on the concept of functions and their domains, offering practical advice on how to approach and solve various mathematical problems. Additionally, the transcript mentions resources for further study and clarifies how to graph exponential and absolute value functions, complete with domain and range in interval notation.
Takeaways
- 📚 The video is a study aid for pre-calculus final exam preparation, focusing on topics like laws of signs and cosines, and triangle problems.
- 🔍 For trigonometry topics, a separate video is recommended, accessible through a YouTube search or a link in the video description.
- ✍️ The video suggests solving problems by pausing and working through them individually before checking solutions against the video.
- 📈 The script covers solving exponential equations by converting bases and using properties of exponents.
- 🔄 It explains finding the inverse function by replacing f(x) with y, switching x and y, and solving for y.
- 📊 The video provides strategies for evaluating logarithmic expressions both mentally and using written methods.
- 🤔 Piecewise functions are discussed, with an example given on how to find the sum of function values at specific points.
- 📈 The concept of continuous compound interest is explained, with a formula provided to calculate the time for investment doubling.
- 🧮 A detailed example is given on calculating the future account value after 40 years with a given interest rate and no withdrawals.
- 🔢 The sum of zeros in a polynomial function is determined by listing potential zeros and using synthetic division.
- 📊 The domain of functions is discussed, with methods for identifying it through inequality solving and number line plotting.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to provide a review for students studying for their pre-calculus final exam, focusing on solving problems that may appear on the exam, including exponential equations, inverse functions, logarithmic expressions, and more.
How does the video approach solving exponential equations?
-The video approaches solving exponential equations by first converting the bases to the same base, then using the properties of exponents to simplify and solve for the variable.
What is the method for finding the inverse function of a given function?
-To find the inverse function, the video suggests replacing f(x) with y, then swapping x and y, solving for y, and finally replacing y with f^(-1)(x) to get the inverse function.
How does the video explain the concept of logarithms?
-The video explains logarithms by providing mental calculations and examples, such as log base 2 of 8 equals 3, and then using these concepts to solve more complex logarithmic expressions.
What is the process for evaluating piecewise functions?
-To evaluate piecewise functions, the video suggests determining which part of the function to use based on the value being evaluated, then applying that specific part of the function to find the result.
How does the video handle logarithmic equations to find the value of x?
-The video handles logarithmic equations by converting them into exponential form, using the properties of logarithms and exponents to isolate and solve for x.
What formula is used to determine the time it takes for an investment to double?
-The formula used is a continuous compounding formula: a = pe^(rt), where a is the future value, p is the principal, r is the annual interest rate (as a decimal), e is Euler's number, and t is the time in years.
How does the video approach the problem of finding the sum of zeros in a polynomial?
-The video approaches this by first listing possible factors of the constant term, testing these factors to see if they result in zero, and then using synthetic division to find the remaining zeros.
What is the method for determining the domain of a function involving a square root?
-The method involves ensuring that the expression under the square root is non-negative, as negative numbers inside a square root do not yield real numbers.
How does the video explain the domain of a rational function?
-The video explains that the domain of a rational function is determined by ensuring the denominator is never zero, which involves factoring the denominator and setting each factor not equal to zero.
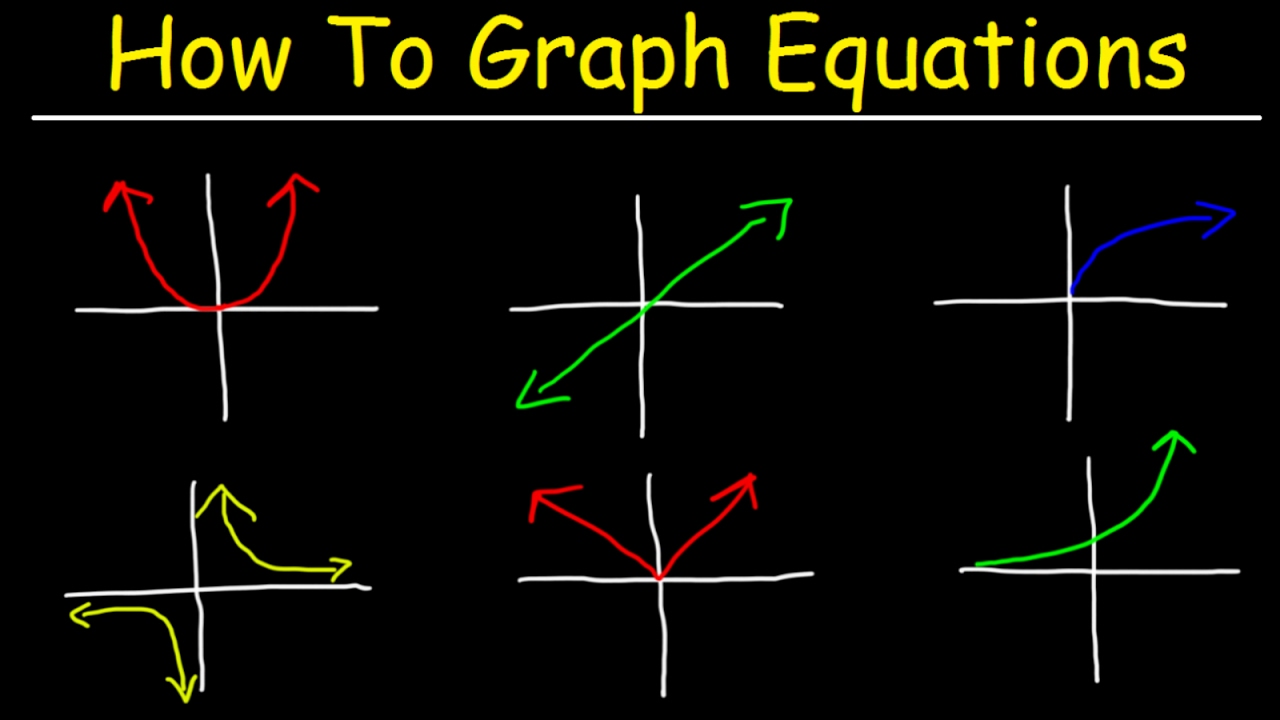
What is the process for graphing an absolute value function?
-The process involves understanding the parent function, applying transformations (shifts and reflections), and plotting key points based on these transformations to sketch the graph.
Outlines
📚 Pre-Calculus Final Exam Review Introduction
This paragraph introduces the video as a study aid for those preparing for a pre-calculus final exam. It mentions that the video does not cover many trick questions but does discuss the law of signs, law of cosines, and some trigonometry problems. The video creator also refers to a separate video dedicated to trigonometry and provides instructions on how to find it through YouTube search or video description links. The paragraph ends with a recommendation to pause the video and attempt problems before checking solutions.
🔢 Solving Exponential and Inverse Functions
This section focuses on solving exponential equations and finding the inverse function of a given function. The process of converting bases and dealing with exponents is explained using a specific example. The method of finding the inverse function by replacing f(x) with y and switching x and y is detailed. The paragraph also includes an example of evaluating the inverse function at a specific point and verifying the result by plugging the result back into the original function. Additionally, it provides two methods for solving a logarithmic expression, one being mental calculation and the other using the properties of logarithms to convert the expression into an exponential form for solving.
📈 Evaluating Logarithmic Expressions and Piecewise Functions
This paragraph continues the mathematical theme by explaining how to evaluate logarithmic expressions using mental calculations and the properties of logarithms. It provides examples of logarithms with different bases and how to find the exponent when the base is known. The paragraph then moves on to discuss piecewise functions, explaining how to determine the correct part of the function to use based on the input value. It concludes with an example of calculating the sum of function values for a piecewise function at specific points.
🧮 Solving Logarithmic Equations and Compound Interest
The paragraph begins with a detailed explanation of converting logarithmic equations into exponential form and solving for the variable. It provides a step-by-step solution to a specific logarithmic equation. Following this, the concept of compound interest is introduced, explaining the formula for continuous compounding and how to solve for the time it takes for an investment to double. The paragraph concludes with an example of calculating the future value of an investment using the given interest rate and time period.
📊 Compound Interest and Mutual Fund Growth
This section delves into the concept of compound interest, specifically focusing on how to calculate the future value of an investment in a mutual fund with a given annual interest rate compounded monthly. The formula for such calculations is provided, and an example is worked out to illustrate the process. The paragraph emphasizes the power of long-term saving and compounding, showing the significant growth of an investment over 40 years without withdrawals.
🔍 Identifying Polynomial Zeros and Function Domains
The paragraph discusses the process of finding the zeros of a polynomial function by listing possible factors of the constant term and testing them to see which yield zero when plugged into the function. It then explains how to use synthetic division to find the remaining zeros once the first zero is identified. The concept of the domain of a function is introduced, with an example provided on how to determine the domain of a function involving a square root. The paragraph concludes with a method for visually representing the domain and range of a function on a number line.
📐 Graphing Exponential Functions and Asymptotes
This section focuses on the methodology of graphing exponential functions, including identifying the horizontal asymptote and using it as a starting point. The paragraph explains how to plot key points based on the function's equation and how to connect these points to form the graph. It also discusses the domain and range of the function, highlighting how to express these using interval notation. The concept of asymptotes is further explored, with the paragraph noting the characteristics of an exponential function's asymptote and how it relates to the function's graph.
Mindmap
Keywords
💡Pre-calculus final exam
💡Law of Signs
💡Law of Cosines
💡Exponential Equations
💡Inverse Functions
💡Logarithmic Expressions
💡Piecewise Functions
💡Continuous Compound Interest
💡Polynomial Zeros
💡Domain of a Function
💡Interval Notation
Highlights
The video is a comprehensive review for students preparing for their pre-calculus final exam.
The video briefly touches on the law of signs and law of cosines, and a few triangle problems.
For those with trigonometry in their exam, there is a dedicated video for review which can be found via a search on YouTube or through the description of the current video.
The video suggests pausing to attempt problems independently before checking the solutions.
The first problem involves solving an exponential equation by converting bases and simplifying.
The second problem explains how to find the inverse function and evaluate it at a given point.
The third problem demonstrates evaluating a logarithmic expression using mental math and properties of logarithms.
The fourth problem involves using a piecewise function to find the sum of function values at specific points.
The fifth problem shows how to convert a logarithmic equation into an exponential equation to solve for x.
The sixth problem discusses the concept of continuous compounding and the time it takes for an investment to double.
The seventh problem calculates the future value of an investment in a mutual fund after a set period at a compounded interest rate.
The eighth problem involves finding the sum of all zeros in a given polynomial function.
The ninth problem explains how to determine the domain of a function involving a square root.
The tenth problem illustrates how to write the domain of a function using interval notation for a rational function.
The eleventh problem tests the ability to solve a logarithmic equation and identify the correct solution.
The twelfth problem demonstrates evaluating a composite function by first finding the inner function's value and then substituting it into the outer function.
The thirteenth problem explains the vertical line test for identifying whether a graph represents a function.
The fourteenth problem involves graphing an absolute value function and identifying its domain and range.
The fifteenth problem guides through graphing an exponential function, determining its domain and range, and identifying asymptotes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: