High School Physics: Free Fall
TLDRThe transcript discusses the concept of freefall, where an object is solely under the influence of gravity, neglecting air resistance. It explains that freefall is characterized by an object accelerating towards Earth at 9.8 m/s^2. The video uses kinematic equations to solve problems related to freefall, such as calculating the distance a brick falls in 3 seconds, the speed of a ball at its maximum height after being thrown upward, the height of a basketball player's jump, and the speed of a ball thrown downward. The examples illustrate the principles of vertical motion, including the symmetry of an object's journey up and down, and the use of initial velocity and acceleration in calculations.
Takeaways
- 📉 Freefall is a motion where an object is solely influenced by gravity, neglecting air resistance.
- 🌍 In freefall, objects accelerate towards the Earth's center at approximately 9.8 m/s², which is the acceleration due to gravity.
- 📌 The kinematic equations are used to solve problems involving objects in constant acceleration during freefall.
- 💫 At the highest point of its trajectory, a freely falling object's velocity is zero due to the brief pause before it starts descending.
- 🔄 There is a symmetry in the motion of an object thrown vertically upwards; it takes the same amount of time to ascend and descend from a given height.
- 🚀 When an object is thrown upwards with an initial velocity, its maximum height can be found using the kinematic equation v² = u² + 2as, where v=0 at the maximum height.
- 📊 The vertical displacement of an object in freefall can be calculated using the equation Δy = ut + 0.5at², with initial velocity (u) being zero.
- 🏀 For an object thrown upwards and returning to the same height, the initial velocity and time taken to ascend are equal to the final velocity and time taken to descend.
- 📈 The final velocity of an object thrown downwards can be calculated using the equation v = u + at, considering the initial velocity (u) and time (t).
- 🤔 To solve more complex problems, it can be helpful to break down the motion into segments, such as analyzing only the ascent or only the descent of the object.
Q & A
What is freefall?
-Freefall is a condition where an object is in constant acceleration due to gravity alone, without any other forces acting on it such as air resistance.
Why is air resistance neglected in the study of freefall?
-Air resistance is neglected in the study of freefall to simplify the analysis, allowing for a focus on the fundamental principles of motion under the influence of gravity alone.
What is the acceleration due to gravity near the Earth's surface?
-The acceleration due to gravity near the Earth's surface is approximately 9.8 m/s^2, directed towards the center of the Earth.
How does the acceleration due to gravity change with distance from the Earth?
-The acceleration due to gravity decreases as one moves further away from the Earth and can vary on different planets due to their mass and size.
What is the initial velocity of an object in freefall?
-The initial velocity of an object in freefall is zero since it starts from rest.
How can you calculate the distance a freely falling object falls in a given time?
-You can use the kinematic equation: Δy = (1/2) * g * t^2, where g is the acceleration due to gravity and t is the time.
What is the significance of symmetry in vertical motion problems?
-Symmetry in vertical motion problems means that the time taken for an object to rise to its highest point is equal to the time it takes to fall back down to the starting height, assuming no air resistance.
How can you find the maximum height reached by an object thrown vertically upward?
-You can use the kinematic equation: Δy = v^2 / (2 * g), where v is the initial velocity of the object and g is the acceleration due to gravity.
What is the final velocity of an object thrown vertically downward with an initial velocity?
-The final velocity of an object thrown vertically downward can be found using the equation: v = v0 + gt, where v0 is the initial velocity, g is the acceleration due to gravity, and t is the time elapsed.
How can you determine the time it takes for a freely falling object to hit the ground from a certain height?
-You can use the kinematic equation: h = (1/2) * g * t^2 to find the height (h) and then solve for t, the time, by rearranging the equation to solve for t: t = sqrt(2h/g).
What happens to the velocity of an object at its highest point in vertical motion?
-At its highest point, the velocity of an object in vertical motion becomes zero momentarily before it starts to fall back down.
Outlines
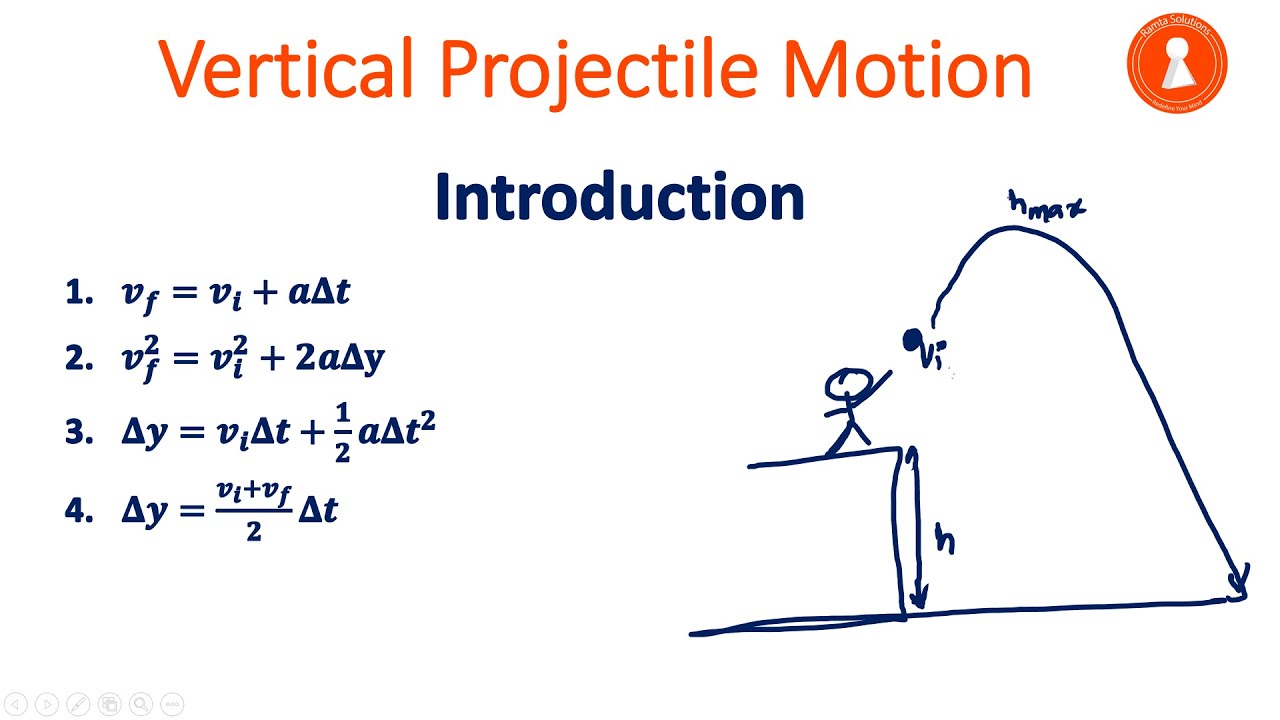
📚 Introduction to Freefall and Kinematic Equations
This paragraph introduces the concept of freefall, explaining it as a scenario where an object is solely influenced by gravity, with air resistance being neglected. It emphasizes that in a true freefall, objects accelerate towards the Earth's center at 9.8 m/s^2. The paragraph sets the stage for using kinematic equations to solve problems involving objects in constant acceleration due to gravity, starting with those at rest and then discussing the implications of initial velocities and the upward motion of objects.
📈 Solving Problems with Falling Objects
The second paragraph delves into the specifics of solving problems related to falling objects. It describes how to use the kinematic equations to calculate the distance a brick falls freely in 3 seconds, considering air resistance negligible. The explanation simplifies the kinematic equation to account for the initial velocity being zero and the acceleration being positive due to gravity. The paragraph further discusses the symmetry of motion for objects moving upward and downward, providing insights into solving more complex problems involving initial velocities and maximum heights reached.
🏀 Vertical Jump Analysis
This paragraph focuses on analyzing the motion of a basketball player jumping for a rebound. It breaks down the vertical motion into two parts—going up and coming down—and uses the symmetry of motion to simplify the problem. The discussion involves calculating the initial velocity of the jump and the height reached using the principles of kinematics. The paragraph also touches on the practicality of the calculated jump height, relating it to a realistic basketball scenario.
🚀 Projectile Motion and Maximum Height
The final paragraph discusses the motion of projectiles, specifically a ball thrown vertically upward and a baseball thrown upward by a player. It explains how to calculate the speed of the ball after being released and the maximum height reached by the baseball. The explanation involves using the kinematic equations to account for the initial velocities, the acceleration due to gravity, and the time elapsed. The paragraph concludes with an invitation for the audience to create their own problems involving dropped or launched objects, encouraging further exploration and practice of the concepts discussed.
Mindmap
Keywords
💡Freefall
💡Constant Acceleration
💡Kinematic Equations
💡Air Resistance
💡Acceleration Due to Gravity
💡Initial Velocity
💡Final Velocity
💡Vertical Displacement
💡Symmetry of Motion
💡Maximum Height
💡Vertically Launched
Highlights
The concept of freefall is introduced, which is an object moving solely under the influence of gravity without any other forces like air resistance.
The acceleration due to gravity is discussed, with its value being 9.8 m/s^2 near the Earth's surface, directed towards the center of the Earth.
The Apollo Mission experiment where a hammer and a feather fall at the same rate on the moon, demonstrating the absence of air resistance, is mentioned.
The kinematic equations are applied to solve problems involving objects in freefall, with the initial velocity being zero and acceleration being gravity.
A brick falling freely from rest for 3 seconds is used as an example to demonstrate how to calculate the distance fallen, using the simplified kinematic equation.
The concept of symmetry in motion is introduced, where the time taken to ascend to the maximum height is equal to the time taken to descend.
A basketball player jumping straight up for 8 seconds is used as an example to illustrate the application of kinematic equations to calculate the height reached.
The problem of a ball thrown vertically upward and reaching a maximum height is solved, demonstrating the use of kinematic equations to find the initial velocity.
A ball thrown straight down from a height of 4 meters with an initial speed is used as an example to calculate the speed of the ball after 7 seconds.
The maximum height reached by a baseball thrown upward with an initial speed of 30 m/s is calculated, using the kinematic equation to find the maximum displacement.
The importance of neglecting air resistance in the context of this course is emphasized for simplicity in problem-solving.
The practical application of the concepts is encouraged by suggesting the creation of a dropped object problem to understand the principles better.
The transcript concludes with a recommendation to visit A+ Physics for more information and practice, highlighting the availability of resources for further learning.
The use of kinematic equations in solving physics problems is demonstrated through various examples, emphasizing the practicality and applicability of the concepts.
The transcript provides a comprehensive overview of the principles of freefall motion, offering a solid foundation for further study in physics.
The concept of gravitational field strength is clarified, explaining that the value of 'g' is not constant and can vary with location and planetary mass.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: