Algebra Basics: What Are Functions? - Math Antics

mathantics
28 Nov 201611:34
EducationalLearning
32 Likes 10 Comments

TLDRIn this Math Antics lesson, Rob introduces the concept of functions in algebra, explaining how they relate one set to another in a specific way. Functions map inputs from a 'domain' to outputs in a 'range', often represented by mathematical equations. The lesson clarifies that a true function assigns exactly one output to each input, disqualifying 'one-to-many' relations. Various examples, including a linear function and the concept of function notation, are used to illustrate the principles, emphasizing the importance of the Vertical Line Test to validate functions and their graphical representation on the coordinate plane.

Takeaways
  • 📚 A function in math is a relationship between two sets, the domain (input set) and the range (output set).
  • 🔢 Sets can be finite or infinite collections of items, often numbers but not limited to them.
  • 📈 Functions map each input value to exactly one output value, following a specific rule or equation.
  • 📊 A function table displays inputs and their corresponding outputs in columns, illustrating the function's behavior.
  • 🏳️‍🌈 The domain and range of a function can be represented visually on a coordinate plane using ordered pairs.
  • 🔍 The 'Vertical Line Test' is used to determine if a graph represents a function by checking for one output per input across the domain.
  • 📌 Functions in algebra often take the form of equations and can be graphed on a coordinate plane.
  • 🔢 The general form of a linear function is y = mx + b, where m is the slope and b is the y-intercept.
  • 📝 Functions can be represented using function notation, such as f(x), to emphasize the input-output relationship.
  • 👉 You can evaluate a function for specific input values by substituting the value into the function's equation.
  • 📖 Understanding functions is fundamental to algebra and allows for solving a variety of mathematical problems.
Q & A

  • What is the definition of a function in mathematics?

    -In mathematics, a function is a relation that connects one set to another set in a specific way. It takes each value from an input set (the domain) and relates it to a value in an output set (the range).

  • How are sets represented visually and notationally?

    -Visually, sets can be shown as a collection of items, while notationally, they are often written inside curly brackets with commas separating the elements, like {1, 2, 3}.

  • What are the two sets involved in a function called?

    -The two sets involved in a function are called the input set (or domain) and the output set (or range).

  • What is a function table and how is it structured?

    -A function table is a table that displays the relationship between inputs and outputs of a function. It typically has two columns: one for input values on the left and one for the corresponding output values on the right.

  • How does the function in the polygon example relate inputs to outputs?

    -In the polygon example, the function relates the name of a polygon to the number of its sides. For instance, if the input is 'triangle', the output is 3, and if the input is 'square', the output is 4.

  • What is the main characteristic of a function that distinguishes it from other relations?

    -A function must produce exactly one output value for each input value. This means it cannot have a 'one-to-many' relation where one input value results in multiple output values.

  • How can you determine if a graph represents a function using the Vertical Line Test?

    -If a vertical line intersects the graph at exactly one point for every possible value of 'x' in the domain, then the graph represents a function. If it intersects at more than one point for some 'x' values, it is not a function.

  • What is the purpose of function notation, such as f(x)?

    -Function notation, like f(x), is a way to represent a function with a specific input variable (x) and to indicate that 'f' is the name of the function, not a variable being multiplied by 'x'. It also allows for easy evaluation of the function for specific input values.

  • How can you evaluate a function for a specific input value?

    -To evaluate a function for a specific input value, you replace the input variable (usually 'x') with the given value in the function's equation. For example, for the function f(x) = 3x + 2, f(4) would be calculated as 3*4 + 2, which equals 14.

  • What is a linear function and what does its graph look like?

    -A linear function is a type of function that has a graph that forms a straight line when plotted on a coordinate plane. An example of a linear function is y = 2x + 1.

  • What are some other types of functions encountered in Algebra?

    -In Algebra, other types of functions include quadratic functions, cubic functions, and trigonometric functions, all of which have distinctive graphs that can be identified and analyzed.

  • What is the domain of the function in the video that does not qualify as a function?

    -The domain of the function y^2 = x does not include negative input values. For positive input values, it can produce two possible output values, which is why it does not qualify as a function.

Outlines
00:00
📚 Introduction to Functions and Sets

This paragraph introduces the concept of functions in mathematics, explaining that a function is a relationship between two sets. It defines a set as a collection of things, which can be numbers or other items, and distinguishes between finite and infinite sets. The paragraph further clarifies the input set (domain) and output set (range) of a function, using the example of a function that maps polygon names to the number of their sides. It also introduces the concept of a function table and basic algebraic functions, emphasizing the rule that a function must map each input to a unique output, disqualifying 'one-to-many' relationships.

05:00
🔍 Understanding Function Properties and Notation

The second paragraph delves into the properties of functions, emphasizing the requirement for each input to have exactly one output, thus defining a 'one-to-one' relationship. It uses the example of the equation y = x + 1 to illustrate a valid function and contrasts it with the equation y squared equals x, which is not a function due to its 'one-to-many' output. The paragraph also explains how functions can be graphed on a coordinate plane and introduces the Vertical Line Test as a method to verify if a graph represents a function. Additionally, it clarifies common function notation, such as f(x) = y, and explains the interchangeable use of 'y' and f(x) in representing the output of a function.

10:03
📈 Graphing Functions and Evaluating Specific Values

The final paragraph discusses the graphical representation of functions, focusing on how different types of functions, including linear, quadratic, cubic, and trigonometric functions, can be plotted on a coordinate plane. It reinforces the concept of the Vertical Line Test as a tool to confirm if a graph represents a function. The paragraph then addresses the use of function notation, particularly the f(x) notation, and explains its purpose in emphasizing the function's relationship with specific input variables. It also demonstrates how to evaluate a function for particular input values, providing examples with the function f(x) = 3x + 2. The paragraph concludes by summarizing the definition of functions and their key components, such as domain and range, and encourages practice with the concepts introduced.

Mindmap
Keywords
💡Functions
In mathematics, a function is a relation that assigns a unique output value to each input value from a given set, known as the domain. It represents a connection between two sets, where every element from the domain is mapped to exactly one element in the range. In the video, functions are introduced as a way to relate one set of inputs to a set of outputs, such as the example of a function that assigns the number of sides to polygon names.
💡Sets
A set in mathematics is a collection of distinct objects, considered as an object in its own right. Sets can consist of numbers, letters, or any other type of objects. In the context of functions, sets are used to define the domain (input values) and the range (output values). The video explains that sets can be finite or infinite and are often visually represented with curly brackets enclosing their elements.
💡Domain
The domain of a function is the set of all possible input values that the function can accept. It defines the range of values that can be used as inputs for the function without resulting in any errors or undefined results. In the video, the domain is referred to as the input set, which is crucial for understanding how a function operates and what values can be used to generate output.
💡Range
The range of a function is the set of all possible output values that result from applying the function to its domain. It is the collection of all outputs that the function can produce. The range is directly related to the function's behavior and the possible results of using it. In the video, the range is discussed as the output set, illustrating the relationship between the input set (domain) and the output set (range).
💡Function Table
A function table is a tabular representation of a function that shows how input values (from the domain) map to output values (in the range). It consists of two columns, one for inputs and one for outputs, with each row showing a single input-output pair. Function tables are useful for visualizing the behavior of a function and understanding its mapping from inputs to outputs.
💡Algebraic Equation
An algebraic equation is a mathematical statement that asserts the equality of two expressions, often involving variables, constants, and various operations such as addition, subtraction, multiplication, and division. In the context of functions, equations can represent the rule or process by which inputs are transformed into outputs.
💡Graph
In mathematics, a graph is a visual representation of the relationship between two variables, where one variable's values are plotted on a horizontal axis (x-axis) and the other's on a vertical axis (y-axis). The graph of a function shows all the input-output pairs as points on a coordinate plane, and by connecting these points, one can visualize the function's behavior. The video explains that different types of functions, such as linear and quadratic functions, have distinct graphical representations.
💡Vertical Line Test
The vertical line test is a method used to determine whether a curve on a coordinate plane represents a function. According to this test, if a vertical line can intersect the curve at no more than one point, then the curve is considered to represent a function. This test checks for the 'one-to-many' relationship, which is not allowed in functions, ensuring that each input value corresponds to exactly one output value.
💡One-to-Many Relation
A one-to-many relation occurs when a single element from one set (the domain) can be associated with multiple elements in another set (the range). This is not allowed in functions because functions must have a one-to-one correspondence between inputs and outputs, meaning each input value can only produce one output value. The video explains that while one-to-many relations exist, they are not considered functions.
💡Function Notation
Function notation is a way of expressing a function using a symbol, typically 'f', followed by parentheses around the input variable. This notation emphasizes that the function is a rule that takes an input and produces a unique output. It is a shorthand that allows for clear communication of the function's relationship between inputs and outputs and is particularly useful when evaluating the function for specific input values.
💡Ordered Pair
An ordered pair is a pair of values that are associated in a specific order, typically denoted as (x, y). In the context of functions and graphs, ordered pairs represent the points on the coordinate plane where the input value (x) is plotted on the horizontal axis, and the output value (y) is on the vertical axis. The order of the pair is important, as (x, y) is different from (y, x) in terms of their representation on the graph.
Highlights

In math, a function is something that relates or connects one set to another set in a particular way.

A set is a group or collection of things, often a collection of numbers.

A function takes each value from an input set (the domain) and relates it to a value in an output set (the range).

Functions are often represented in a function table with two columns, one for input values and one for output values.

The function in the example relates the name of a polygon to its number of sides.

Algebraic functions usually relate one variable to another in the form of an equation, like y = 2x.

For each input value, the output value is twice as big in the function y = 2x.

Functions are not allowed to have 'one-to-many' relations, where one input value could result in many different output values.

A function produces only one output value for each input value, relating a member of the input set to exactly one member of the output set.

The equation y = x + 1 is an example of a linear function, which graphs as a straight line on the coordinate plane.

There are various types of functions in Algebra with interesting graphs, such as quadratic, cubic, and trigonometric functions.

The Vertical Line Test helps determine if a graph is a function by checking if a vertical line intersects the graph at exactly one point for every 'x' value in the domain.

Functions can be represented using function notation, such as f(x) = y, where 'f' is the name of the function, 'x' is the input, and 'y' is the output.

The interchangeable use of f(x) and 'y' in function notation highlights dealing with a function and allows for easy evaluation of the function for specific input values.

The basic concept of a function in math is that it relates an input value to exactly one output value.

The domain is the set of all input values for a function, and the range is the set of output values.

Algebraic functions can be graphed on the coordinate plane by treating input and output values as ordered pairs.

The video provides a basic introduction to functions, which is essential for working with them in Algebra.

Transcripts

Browse More Related Video

Introduction to Functions (Precalculus - College Algebra 2)

Back to Algebra: What are Functions?

One to One Functions (Precalculus - College Algebra 50)

Calculus made EASY! 5 Concepts you MUST KNOW before taking calculus!

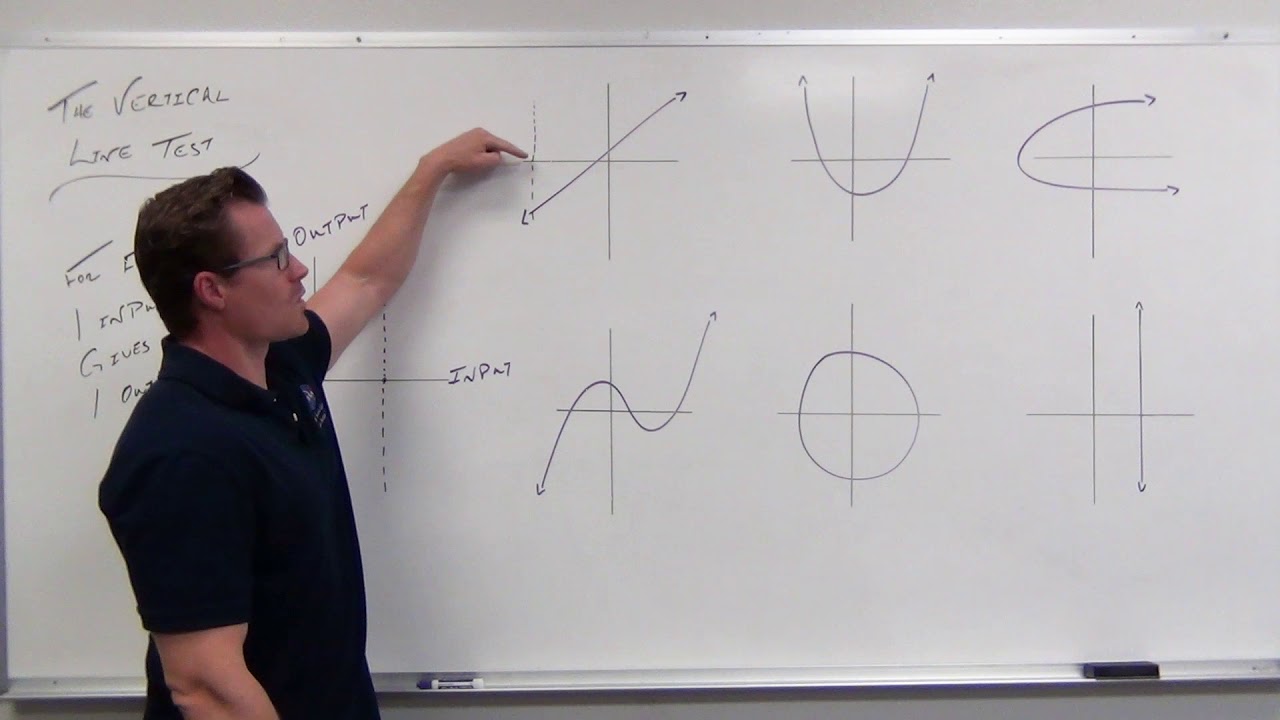
Using the Vertical Line Test (Precalculus - College Algebra 6)

Relations, Mappings & Functions.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Algebra BasicsFunction ConceptsInput-Output MappingDomain and RangeFunction NotationMath EducationVisual LearningLinear FunctionsVertical Line TestMath Antics