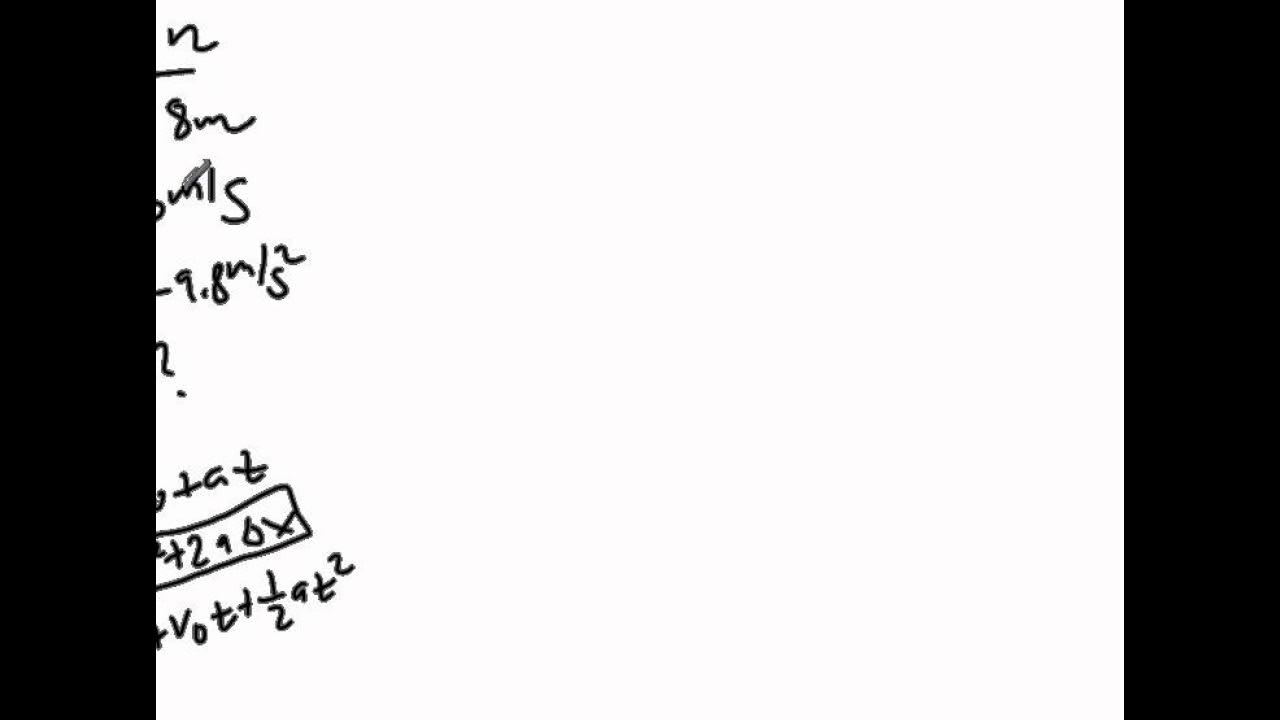AP Physics B Kinematics Presentation #35

The New Jersey Center for Teaching and Learning
26 Jun 201203:42
EducationalLearning
32 Likes 10 Comments

TLDRThe script describes a physics problem involving a ball thrown vertically downward from a cliff with an initial speed of 8 m/s. It takes 6 seconds for the ball to hit the ground, and the problem is solved using the equations of motion under gravity. The initial velocity is considered negative due to the downward direction, and the acceleration due to gravity is 9.8 m/s². By applying the kinematic equations, the script calculates the initial height of the cliff to be 224 meters, providing a clear demonstration of how to solve for vertical displacement in a physics context.

Takeaways
  • 📚 The problem involves a ball thrown vertically downward from a cliff with an initial speed of 8 m/s.
  • 📉 The initial velocity is considered negative due to the downward direction of the throw.
  • ⏱️ It took 6 seconds for the ball to reach the ground from the cliff's edge.
  • 📉 The acceleration due to gravity is -9.8 m/s², acting downwards.
  • 🔍 The final height of the ball when it hits the ground is 0 meters.
  • 🔑 The formula used to solve for the initial height (y₀) is derived from the kinematic equation: y = y₀ + v₀t + 1/2at².
  • 🚫 The term involving the initial height (y₀) is canceled out since the final height is 0 meters.
  • 🔢 The equation simplifies to y₀ = v₀t - 1/2at², which is used to find the initial height.
  • 🧮 Plugging in the given values, the calculation for y₀ results in a height of 224 meters.
  • 📈 The calculation involves multiplying the initial velocity by time and subtracting the product of half the acceleration, time squared.
  • 📝 The result indicates that the cliff from which the ball was thrown is 224 meters high.
Q & A

  • What is the initial velocity of the ball when it is thrown vertically down from the cliff?

    -The initial velocity of the ball is -8 m/s, with the negative sign indicating the downward direction.

  • What is the acceleration acting on the ball during its fall?

    -The acceleration acting on the ball is the acceleration due to gravity, which is 9.8 m/s^2.

  • How long does it take for the ball to reach the ground after being thrown?

    -It takes the ball 6 seconds to reach the ground.

  • What is the final height of the ball when it reaches the ground?

    -The final height of the ball when it reaches the ground is 0 meters.

  • What is the formula used to calculate the height of the cliff from which the ball was thrown?

    -The formula used to calculate the height of the cliff is y = y0 + vt + 0.5at^2, where y0 is the initial height, v is the initial velocity, a is the acceleration, and t is the time.

  • Why is the initial velocity given a negative value in the formula?

    -The initial velocity is given a negative value because it is in the downward direction, which is considered negative in the context of the formula.

  • How is the formula for the height of the cliff simplified in this scenario?

    -The formula is simplified by recognizing that the final height (y) is 0 meters, thus eliminating the y0 term, and rearranging to solve for y0.

  • What is the value of the term 'vt' in the formula when calculating the height of the cliff?

    -The value of 'vt' is -48 m, calculated as -8 m/s multiplied by 6 seconds.

  • What is the term '0.5at^2' in the formula, and what is its value in this scenario?

    -The term '0.5at^2' represents the distance the ball falls due to gravity. Its value in this scenario is 176.832 m, calculated as 0.5 * 9.8 m/s^2 * (6 s)^2.

  • What is the calculated height of the cliff from which the ball was thrown?

    -The calculated height of the cliff is 224 meters, obtained by adding the values of 'vt' and '0.5at^2'.

  • What is the significance of the negative sign in the calculation of the height of the cliff?

    -The negative sign in the calculation indicates that the initial velocity is in the opposite direction of the positive y-axis, and when added to the positive value of '0.5at^2', it gives the correct height from which the ball was thrown.

Outlines
00:00
📚 Calculating Cliff Height from Free Fall

The script explains a physics problem involving a ball thrown vertically downwards from a cliff. Given the initial velocity of 8 m/s, the acceleration due to gravity (9.8 m/s²), and the time taken to reach the ground (6 seconds), the problem is approached using kinematic equations. The initial and final positions, initial velocity, time, and acceleration are identified, and the equation y = y₀ + v₀t + 1/2at² is simplified to solve for the initial height (y₀). The calculation results in the cliff being 224 meters high.

Mindmap
Keywords
💡Vertical motion
Vertical motion refers to the movement of an object in a direction perpendicular to the surface of the Earth, either upwards or downwards. In the context of the video, the ball is thrown vertically down, which is a type of vertical motion. The script discusses the physics of this motion, particularly focusing on the descent of the ball from the cliff.
💡Initial velocity
Initial velocity is the speed of an object at the start of its motion. In the video script, the initial velocity of the ball is given as 8 m/s, indicating the speed at which it was thrown down from the cliff. This concept is crucial for understanding the subsequent calculations of the ball's motion under gravity.
💡Acceleration due to gravity
Acceleration due to gravity is the rate at which an object in free fall accelerates towards the Earth's surface, approximately 9.8 m/s². The script uses this value to calculate the distance the ball falls, as it is the constant acceleration acting on the ball during its descent.
💡Final velocity
Final velocity is the speed of an object at the end of its motion. Although not explicitly calculated in the script, the concept is implied when discussing the equations of motion. The final velocity of the ball would be the speed just before it hits the ground, which is influenced by both its initial velocity and the acceleration due to gravity.
💡Time
Time is the duration for which the motion occurs. In the script, it is stated that the ball takes 6 seconds to reach the ground. Time is a key variable in the equations of motion used to calculate the distance fallen by the ball.
💡Position
Position refers to the location of an object in space. The script mentions the initial and final positions of the ball, with the initial position being the height of the cliff (unknown) and the final position being the ground (0 meters).
💡Equations of motion
Equations of motion are mathematical formulas that describe the relationship between an object's displacement, velocity, acceleration, and time. The script uses these equations to solve for the height of the cliff, specifically the equation y = y0 + v0*t + 0.5*a*t², where y0 is the initial position, v0 is the initial velocity, a is the acceleration, and t is the time.
💡Displacement
Displacement is the change in position of an object. In the context of the video, displacement is used to describe the distance the ball falls from the cliff to the ground, which is the height of the cliff that the script aims to calculate.
💡Free fall
Free fall is the motion of an object when it is subject only to the force of gravity, without any other forces acting on it (like air resistance). The script describes the ball's motion as a free fall, which simplifies the calculations by allowing the use of the basic equations of motion.
💡Calculation
Calculation refers to the process of computing a value or result using mathematical methods. The script involves several calculations to determine the height of the cliff, using the given values for initial velocity, acceleration due to gravity, and time.
💡Height of the cliff
The height of the cliff is the final value that the script is trying to determine. It is the initial height from which the ball is thrown and is calculated using the equations of motion and the given parameters of the ball's descent.
Highlights

A ball is thrown vertically down from the edge of a cliff with an initial speed of 8 m/s.

The ball reaches the ground after 6 seconds, indicating the time of flight.

The initial velocity is considered negative due to the downward direction of the throw.

Gravity's acceleration is taken as 9.8 m/s², the standard value on Earth.

The final height of the ball when it hits the ground is 0 m.

The problem involves solving for the initial height of the cliff (y₀).

The kinematic equation v = v₀ + at is used to relate initial velocity, acceleration, and time.

The equation y = y₀ + v₀t + 1/2at² is identified as the key formula for the problem.

The final position (y) is set to 0 m, simplifying the equation to solve for y₀.

The simplified equation y₀ = v₀t + 1/2at² is derived to find the initial height.

Plugging in the given values, the calculation for y₀ begins with the term -8 m/s * 6 s.

The calculation continues with the term -1/2 * 9.8 m/s² * (6 s)².

The calculation results in a positive value for y₀, indicating the height from which the ball was thrown.

The final calculated height of the cliff is 224 meters.

The problem demonstrates the application of basic physics principles to real-world scenarios.

The solution process emphasizes the importance of direction in kinematic equations.

The problem showcases the step-by-step approach to solving physics problems involving motion.

The final answer is derived through a combination of algebraic manipulation and substitution.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #32

High School Physics: Free Fall

Rectilinear Motion Problems - Distance, Displacement, Velocity, Speed & Acceleration

AP Physics B Kinematics Presentation #34

AP Physics B Kinematics Presentation #38

Two Dimensional Motion Problems - Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics CalculationVertical MotionFree FallCliff HeightInitial VelocityGravity AccelerationTime TakenMotion AnalysisFalling ObjectEducational Content