Introduction to Transformations of Functions
TLDRThis informative script introduces the concept of functions and their transformations, emphasizing the importance of understanding functions for real-life applications. It defines a function as a numerical relationship with a unique output for every input, using the notation f(x). The script covers parent functions like constant, linear, absolute value, and quadratic functions, explaining their key features and how to identify them using the vertical line test. It then delves into transformations, detailing horizontal and vertical translations, stretches, shrinks, and reflections, providing rules for interpreting mathematical equations and visualizing the resulting graphs.
Takeaways
- 📚 Functions are numerical relationships where each input (X) has exactly one output (Y).
- 🛒 Real-life applications of functions require consistency, like a price for an item, to be useful.
- 📏 The vertical line test checks if a graph represents a function by seeing if the line crosses the graph more than once.
- 🏩 Parent functions are basic function forms like constant, linear, absolute value, and quadratic functions that can be transformed.
- 🌈 Constant functions are represented by horizontal lines, with every X value mapping to the same Y value.
- 🚦 Linear functions are characterized by straight lines with constant slopes, starting at (0,0) for the parent function.
- 🔄 Absolute value functions have a V-shape, with a vertex at (0,0), representing distances from numbers to zero.
- 🥚 Quadratic functions are U-shaped and have a vertex at (0,0), with slopes that change as you move left or right from the vertex.
- 🔄 Transformations are changes made to parent functions, including horizontal and vertical translations, stretches, shrinks, and reflections.
- 📈 Transformation rules apply to all functions: vertical stretches/shrinks change the Y-axis, horizontal stretches/shrinks change the X-axis, and reflections flip the graph over the X or Y axis.
- 🧩 Describing transformations involves identifying and applying the rules in the order they appear in the function's equation.
Q & A
What is the definition of a function in mathematics?
-A function is a numerical relationship where every input (X value) has exactly one output (Y value). It is a rule or a mapping that assigns to each element of a set (the domain) exactly one element of another set (the range).
Why is it important for a function to have a unique output for each input?
-It is important because functions are used to model real-life situations where a unique output for each input ensures consistency and predictability. For example, in pricing, if different customers were charged different prices for the same item, it would lead to confusion and unfairness.
How is a function represented symbolically?
-A function is commonly represented by a symbol like f(X), G(X), or H(X), where 'f', 'g', or 'h' are names for the function and 'X' represents the input variable.
What is the vertical line test and how does it help in identifying functions?
-The vertical line test is a method to determine if a graphical representation is a function. You draw a vertical line and see if it crosses the graph more than once. If it does, it fails the test, indicating that the graph does not represent a function since a function should not cross a vertical line at any point.
What is a constant function and what does its graph look like?
-A constant function is a function where every input value 'x' maps to the same output value 'y'. Its graph is a horizontal line, as all the output values are the same, regardless of the input.
What are the key features of a linear function?
-A linear function has the form f(x) = mx + b, where 'm' is the constant slope and 'b' is the y-intercept. Its graph is a straight line with a constant slope, passing through the origin (0,0) if 'b' is zero.
How does the absolute value function differ from other functions in terms of its graph?
-The absolute value function has a V-shape graph with its vertex at the origin (0,0). It represents the distance of a number from zero and consists of two straight lines that meet at the vertex, with a constant slope on each side of the x-axis.
What is a quadratic function and what characterizes its graph?
-A quadratic function is defined by an equation with the highest power of the variable being squared, such as f(x) = ax^2 + bx + c. Its graph is a U-shape, known as a parabola, which can open upwards or downwards depending on the coefficient 'a'.
What are the five types of transformations that can be applied to functions?
-The five types of transformations are: horizontal translations (shifts left or right), vertical translations (shifts up or down), horizontal stretches or shrinks, vertical stretches or shrinks, and reflections over the x-axis or y-axis.
How do you interpret a horizontal stretch or shrink in a function?
-A horizontal stretch or shrink is interpreted by multiplying the input variable 'x' by a factor 'k'. If 'k' is greater than 1, it stretches the graph horizontally; if 'k' is between 0 and 1, it shrinks the graph horizontally. The transformation is represented as f(x/k) for a stretch and f(kx) for a shrink.
What happens when you add or subtract a value inside the parentheses of a function?
-When you add or subtract a value inside the parentheses, it results in a horizontal shift of the graph. Adding a value shifts the graph to the right (positive direction), while subtracting shifts it to the left (negative direction).
How do you determine if a function is reflected over the x-axis or y-axis?
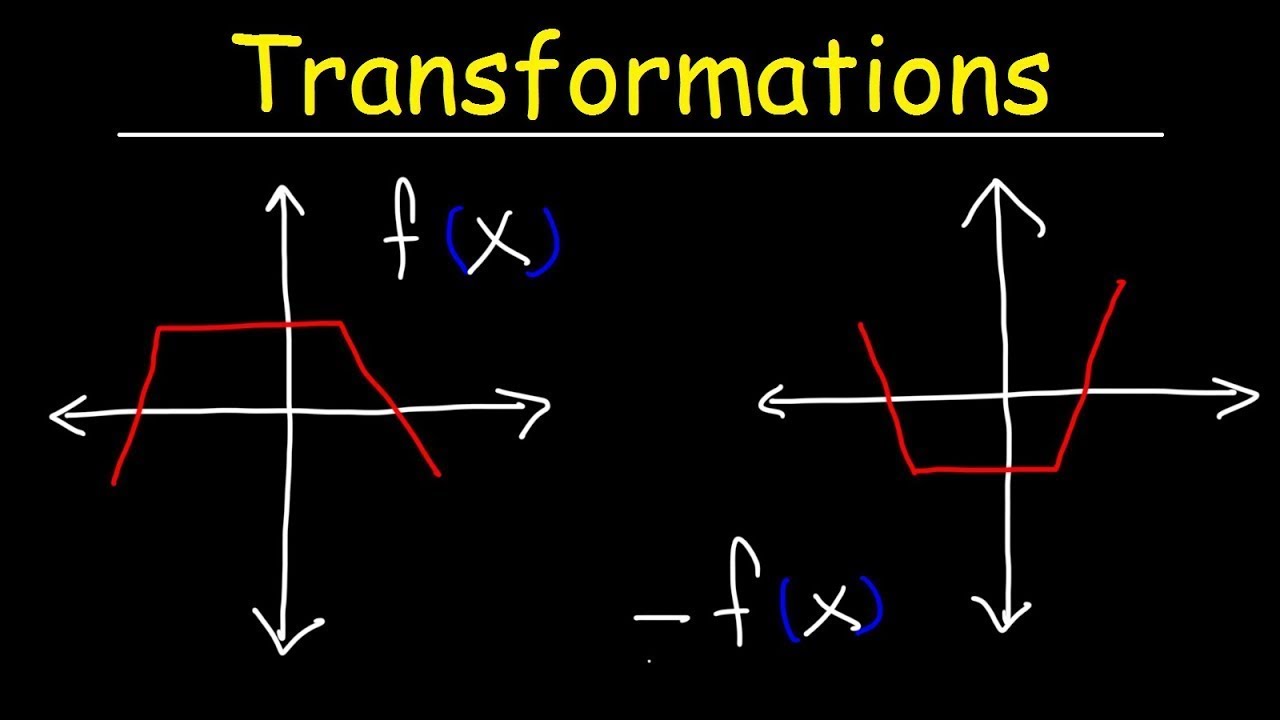
-A function is reflected over the x-axis if the 'x' variable is multiplied by a negative (f(-x)). Conversely, a reflection over the y-axis occurs when the entire function is multiplied by a negative (-f(x)).
Outlines
📚 Introduction to Functions and Transformations
This paragraph introduces the concept of functions, emphasizing their importance in mathematics and real-life applications. It defines a function as a numerical relationship where each input (X) corresponds to exactly one output (Y). The video uses the example of buying peanuts to illustrate the need for a consistent output for each input in a function. The formal definition of a function is presented, and the symbol f(X) is introduced as a common notation for functions. The concept is further explained using the vertical line test, which helps determine if a given graph represents a function. The paragraph concludes by highlighting the importance of understanding parent functions to graph and interpret any function.
📈 Understanding Parent Functions and Their Characteristics
This paragraph delves into different types of parent functions, starting with the constant function, which is represented by a horizontal line and has the same Y value for every X value. The linear function is introduced next, characterized by a straight line and a constant slope, with the parent function being f(X) = X. The absolute value function is then discussed, with its V-shaped graph and vertex at the origin (0,0), emphasizing the positive distance from any number to zero. Lastly, the quadratic function is introduced, characterized by a U-shaped graph with a changing slope and a vertex at (0,0). The paragraph outlines the importance of understanding these parent functions to graph and interpret more complex functions through transformations.
🔄 Transformations: Horizontal, Vertical, and Reflective Changes
This paragraph focuses on the process of transformations, which involves changing a parent function in various ways. Five types of transformations are discussed: horizontal and vertical translations (shifts), horizontal and vertical stretches or shrinks, and reflections over the X or Y axis. The rules for interpreting transformations are explained, with horizontal translations involving shifts in the opposite direction of the coefficient inside the parentheses, and vertical translations resulting from adding or subtracting from the entire function. The paragraph also clarifies that multiplying the function by a factor affects the vertical stretch or shrink, while multiplying inside the parentheses affects the horizontal stretch or shrink. The concept is illustrated with examples, showing how to identify and apply transformations to parent functions.
🎯 Applying Transformation Rules to Specific Functions
The paragraph concludes with examples demonstrating how to apply the transformation rules to specific functions. It starts by identifying the parent function based on the given equation and then sequentially applies each transformation, such as vertical stretches, horizontal shifts, and reflections. The examples illustrate how to interpret coefficients outside and inside the parentheses, the impact of adding or subtracting from the function, and the effect of squaring a negative number on quadratic functions. The paragraph emphasizes the importance of practice in understanding and applying these transformation rules for various functions throughout the year.
Mindmap
Keywords
💡Functions
💡Vertical Line Test
💡Parent Functions
💡Constant Function
💡Linear Function
💡Absolute Value Function
💡Quadratic Function
💡Transformations
💡Horizontal Translations
💡Vertical Stretches/Shrinks
💡Reflections
Highlights
Introduction to functions and their transformations.
A function is a numerical relationship where each input has exactly one output.
The real-life importance of functions is exemplified by consistent outputs for identical inputs, like grocery pricing.
The formal definition of a function and the notation f(x).
The vertical line test to determine if a graph represents a function.
Constant functions are horizontal lines with every x value yielding the same y value.
Linear functions are characterized by straight lines and constant slopes.
Absolute value functions have a V-shape with a vertex at the origin and represent distances from zero.
Quadratic functions are U-shaped and have a vertex at the origin with changing slopes.
Transformations of functions include horizontal and vertical translations, stretches, shrinks, and reflections.
The rule for vertical stretches or shrinks: multiply the function by a factor.
Horizontal stretches or shrinks involve multiplying the x inside the function by the reciprocal of the factor.
Horizontal shifts in functions are influenced by additions or subtractions inside the parentheses, moving in the opposite direction.
Vertical shifts are caused by additions or subtractions outside the parentheses, affecting the entire function.
Reflections occur by multiplying the function by a negative, reflecting over the x or y axis.
Quadratic functions with a negative coefficient squared result in no visible change in appearance when reflected over the x-axis.
Understanding these concepts allows for the interpretation and manipulation of any function throughout the year.
Transcripts
Browse More Related Video
Transformations of Functions | Precalculus

Graphing Rational Functions with Transformations (Precalculus - College Algebra 39)

Precalculus Introduction, Basic Overview, Graphing Parent Functions, Transformations, Domain & Range

Ch. 2.6 Transformations of Functions

Graphs You Must Know (Precalculus - College Algebra 13)

Introduction to Graph Transformations (Precalculus - College Algebra 14)
5.0 / 5 (0 votes)
Thanks for rating: