Standing Waves on a String, Fundamental Frequency, Harmonics, Overtones, Nodes, Antinodes, Physics

The Organic Chemistry Tutor

27 Nov 201640:16

EducationalLearning

32 Likes 10 Comments

TLDRThis informative video delves into the concept of standing waves, explaining their creation and characteristics using a string model. It details the relationship between the number of standing waves (n), wavelength, and frequency, highlighting the fundamental frequency and harmonics. The video also explores the equations necessary to calculate various properties of standing waves and discusses nodes and antinodes. Practical examples are used to demonstrate the calculation of frequencies and wavelengths, providing a comprehensive understanding of standing wave patterns.

Takeaways

🌟 Standing waves are patterns that appear stationary because they oscillate without moving in the x-direction, fixed at both ends.
📶 The number of standing waves (n) in a pattern is directly related to the frequency (f) and inversely related to the wavelength (λ).
🎵 The fundamental frequency (f1) is the first harmonic and serves as the basis for calculating higher harmonics, which are multiples of the fundamental frequency.
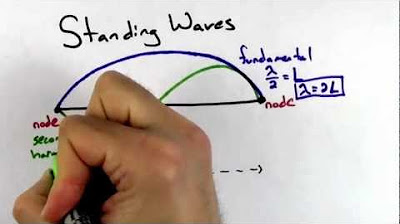
🌀 The wavelength of a standing wave is given by the equation λ = 2L/n, where L is the length of the string and n is the number of standing waves.
📊 The frequency of a standing wave can be found using the equation f = v/λ, where v is the wave speed and λ is the wavelength.
🧵 The speed of a wave on a string is determined by the tension force and the linear density of the string, with the equation v = √(T/m), where T is the tension and m is the linear density.
📌 Nodes are points of zero amplitude within a standing wave pattern, while antinodes are points of maximum displacement.
🔄 The number of nodes in a standing wave pattern is always one more than the number of standing waves (n+1), and the number of antinodes equals the number of standing waves (n).
🔢 To find the length of a string for a given standing wave, use the equation L = nλ/2, which requires knowledge of the number of standing waves and their wavelength.
🌈 The velocity of a wave, wavelength, and frequency are interconnected, and knowing any two of these values allows for the calculation of the third.
📈 The relationship between the different harmonics and their corresponding wavelengths is such that as the harmonic number increases, the wavelength decreases and the frequency increases.

Q & A

What is a standing wave and how is it different from other types of waves?
-A standing wave is a wave pattern that appears to be stationary, not moving in the x-direction. It is different from other types of waves because it is fixed at both ends and does not propagate or travel through space. This is due to the superposition of waves reflecting back and forth between two fixed points, creating nodes and antinodes.
How can you create a standing wave on a string?
-A standing wave can be created on a string by attaching it to two fixed ends and applying a tension force. When the string is plucked or disturbed and then released, it vibrates and forms a standing wave pattern with nodes and antinodes along its length.
What is the relationship between the number of standing waves (n) and the length of the string (L)?
-The length of a standing wave pattern is directly related to the number of standing waves (n) and the length of the string (L). The equation that relates these is L = (n * λ) / 2, where λ is the wavelength. This means that the length of the string must be an integer multiple of half the wavelength to support standing waves.
How does the frequency of a standing wave relate to its wavelength?
-The frequency (f) of a standing wave is inversely proportional to its wavelength (λ). This relationship is described by the equation f = v / λ, where v is the wave speed. As the wavelength decreases, the frequency increases, and vice versa.
What are the fundamental frequency and harmonics in the context of standing waves?
-The fundamental frequency (f1) is the lowest frequency at which a standing wave can vibrate. The harmonics, also known as overtones, are integer multiples of the fundamental frequency (f2 = 2 * f1, f3 = 3 * f1, etc.). Each harmonic corresponds to a different number of standing waves across the string.
What is the equation for calculating the wavelength of a standing wave?
-The equation for calculating the wavelength (λ) of a standing wave is λ = 2L / n, where L is the length of the string and n is the number of standing waves. This equation is derived from the fact that the length of the string must accommodate an integer number of half-wavelengths.
What are nodes and antinodes in a standing wave, and how do they relate to constructive and destructive interference?
-Nodes are points on a standing wave where the amplitude is zero, and antinodes are points where the maximum displacement occurs, having the highest amplitude. Constructive interference occurs at antinodes, where the amplitudes of the interfering waves add together, and destructive interference occurs at nodes, where the amplitudes cancel each other out.
How can you find the speed of a wave knowing the tension and the linear density of the string?
-The speed of a wave (v) on a string can be calculated using the equation v = √(T / (μ / L)), where T is the tension force, μ is the linear density of the string (mass per unit length), and L is the length of the string. The square root of the ratio of tension to the inverse product of linear density and length gives the wave speed.
What is the relationship between the speed of a wave, its wavelength, and its frequency?
-The speed of a wave (v), its wavelength (λ), and its frequency (f) are related by the equation v = λf. This equation shows that the speed of a wave is equal to the product of its wavelength and frequency.
How can you determine the number of nodes and antinodes in a standing wave pattern?
-In a standing wave pattern, the number of nodes is always equal to the number of standing waves (n) plus one, and the number of antinodes is equal to the number of standing waves (n). For example, a standing wave with two loops will have three nodes and two antinodes.
What is the formula to calculate the frequency of the nth harmonic of a standing wave?
-The frequency of the nth harmonic (fn) of a standing wave can be calculated using the formula fn = n * f1, where f1 is the fundamental frequency. This shows that the frequency of a harmonic is directly proportional to its harmonic number and the fundamental frequency.
How can you find the wavelength of the first harmonic given the wavelength of a higher harmonic?
-If you know the wavelength (λn) of the nth harmonic, you can find the wavelength of the first harmonic (λ1) using the equation λ1 = λn * n. This is because the wavelength of a harmonic is inversely proportional to its harmonic number.

Outlines

00:00

🌊 Introduction to Standing Waves

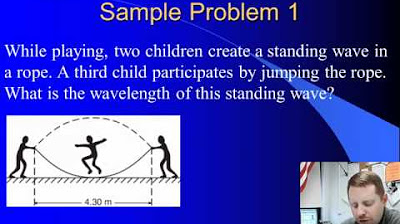
This paragraph introduces the concept of standing waves, explaining how they are created on a string fixed at both ends with tension. It describes different types of standing waves and their appearances, emphasizing that standing waves seem stationary due to their fixed ends. The relationship between the number of standing waves (n), length (l), and wavelength is introduced, with the equation l = n * (wavelength) / 2. The concept of natural frequencies and harmonics is also touched upon, setting the foundation for further discussion.

05:01

📏 Wavelength and Frequency Relationships

This section delves into the mathematical relationships between wavelength, frequency, and the number of standing waves. It explains how the fundamental frequency (f1) and harmonics (fn) are related, with fn being n times f1. The wavelength is shown to be inversely proportional to the number of standing waves, with the equation λ = 2l / n. The concept of natural frequencies is further explored, and the velocity of a wave is related to its wavelength and frequency, with the equation v = wavelength * frequency.

10:03

🎵 Harmonic Analysis and Equation Derivation

This paragraph focuses on the analysis of harmonics and the derivation of key equations. It explains how to find any harmonic frequency using the fundamental frequency and the number of standing waves. The derivation of the equation for wave velocity is discussed, which is based on tension force and linear density. The paragraph also introduces the concept of nodes and antinodes in standing wave patterns, explaining their significance in terms of constructive and destructive interference.

15:04

🔢 Calculation of Harmonics and Wavelengths

This section provides examples of calculating harmonic frequencies and wavelengths for standing waves. It demonstrates how to find the fundamental frequency and subsequent harmonics, as well as the corresponding wavelengths. The relationship between wave speed, wavelength, and frequency is used to solve for unknown values in various scenarios. The importance of these calculations in understanding standing wave behavior is emphasized.

20:06

📐 Applications of Wave Equations

This paragraph discusses the practical application of wave equations in determining characteristics of standing waves, such as the length of the string, wavelength, and frequency. It provides a comprehensive overview of the six main equations essential for analyzing standing waves. The concept of nodes and antinodes is revisited, with an explanation of how to determine their number in a standing wave pattern.

25:07

🌟 Advanced Harmonic and Wave Speed Calculations

This section presents more complex calculations involving harmonics, wavelengths, and wave speeds. It covers scenarios where the number of loops (standing waves) and their corresponding frequencies or wavelengths are given, and it explains how to find related wave properties. The calculations involve the use of multiple equations and the concept of linear density to derive wave speed and tension force.

30:09

📚 Summary and Study Tips

In conclusion, the paragraph provides a brief recap of the key concepts and equations discussed throughout the video. It encourages viewers to practice applying these concepts to ensure understanding and preparation for exams. The goal is to equip viewers with the knowledge and tools necessary to analyze and solve problems related to standing waves effectively.

Mindmap

Keywords

💡Standing Waves

Standing waves are a particular type of wave pattern that appears to be stationary, even though the individual particles in the medium (like a string) are still moving. They are created when a wave reflects back upon itself, leading to a scenario where the wave seems not to move in the x-direction. This concept is central to the video as it explains the fundamental nature of the wave patterns being discussed.

💡String Fixed at Both Ends

A string fixed at both ends is a critical setup for the creation of standing waves. When such a string is subjected to a tension force and then plucked, it generates a standing wave pattern. The fixed ends act as boundaries that reflect the wave back onto itself, which is essential for the formation of standing waves.

💡Wavelength

Wavelength is the distance between two consecutive points in a wave that are in the same phase, such as two crests or two troughs. It is a fundamental property of waves and is directly related to the wave's frequency and speed. In the context of standing waves, the wavelength is associated with the length of the string and the number of loops (standing waves) present.

💡Frequency

Frequency refers to the number of complete wave cycles that pass a given point in a unit of time, typically measured in Hertz (Hz). In the context of standing waves, the frequency is related to the natural or resonant frequencies of the string, with the fundamental frequency being the lowest and the harmonics being multiples of the fundamental frequency.

💡Harmonics

Harmonics, in the context of wave patterns, refer to the multiple frequencies that are integer multiples of the fundamental frequency. Each harmonic corresponds to a specific number of standing waves on the string, with the first harmonic being the fundamental frequency and subsequent harmonics having frequencies that are double, triple, etc., that of the fundamental.

💡Nodes and Antinodes

Nodes and antinodes are specific points on a standing wave. Nodes are locations where the amplitude of the wave is zero, meaning there is no displacement, while antinodes are points of maximum displacement. In a standing wave pattern, nodes and antinodes alternate, and the number of nodes is always one more than the number of loops (or standing waves), while the number of antinodes matches the number of loops.

💡Wave Speed

Wave speed is the rate at which a wave or any disturbance travels through a medium. It is determined by the properties of the medium through which the wave is traveling. In the case of mechanical waves, like those traveling through a string, the wave speed is dependent on the tension in the string and the mass per unit length of the string.

💡Wave Equations

Wave equations are mathematical representations that describe the behavior of waves. They relate various properties of waves, such as wavelength, frequency, speed, and amplitude, and are essential for understanding and predicting wave behavior. The video introduces several key equations that are used to calculate different aspects of standing waves on a string.

💡Resonant Frequencies

Resonant frequencies are the specific frequencies at which a system naturally vibrates. When a system is driven at or near its resonant frequency, it exhibits large amplitude oscillations. In the context of the video, resonant frequencies are the natural frequencies at which the string vibrates to produce standing waves.

💡Constructive and Destructive Interference

Constructive and destructive interference are phenomena that occur when two waves meet. Constructive interference happens when the crest of one wave aligns with the crest of another, resulting in a larger amplitude. Destructive interference occurs when the crest of one wave aligns with the trough of another, leading to a reduction in amplitude or even cancellation.

💡Linear Density

Linear density is the mass per unit length of a material. It is a crucial factor in determining the wave speed on a string, as it affects how the tension is distributed along the string. The linear density, along with the tension force, dictates how waves will propagate through the string.

Highlights

Standard waves are created by applying tension and releasing a string, resulting in a pattern that appears to move or stand still depending on the conditions.

Standing waves appear stationary because they do not move in the x-direction, unlike waves that move along the x-axis.

The number of standard waves in a pattern is indicated by 'n', and each has the same length as the string they are created on.

The wavelength (λ) of a standing wave is related to the length of the string (L) and the number of standard waves (n) by the equation λ = 2L/n.

Standing waves occur at natural or resonant frequencies, with the fundamental frequency (f1) being the lowest.

Higher harmonics (fn) are integer multiples of the fundamental frequency (f1), with fn = n * f1.

The wavelength of a standing wave decreases as the number of standard waves (n) increases, while the frequency increases.

Constructive interference occurs at antinodes where amplitude is maximum, and destructive interference occurs at nodes where amplitude is minimum.

The number of nodes in a standing wave pattern is always one more than the number of standard waves (n).

The number of antinodes in a standing wave pattern is equal to the number of standard waves (n).

The velocity of a wave is determined by the tension force and the linear density of the medium, with v = sqrt(T/μ), where T is tension and μ is linear density.

The speed of a wave is constant for a given medium and is equal to the wavelength times the frequency, v = λf.

To find the length of a string for a given standing wave, use the equation L = nλ/2, where n is the number of standard waves and λ is the wavelength.

The fundamental frequency can be found from a higher harmonic using the equation f1 = fn/n.

The wavelength of the first harmonic (λ1) can be calculated from a higher harmonic's wavelength (λn) using λ1 = λn * n.

The tension force required to produce a standing wave can be calculated using F = (μL * v^2) / L, where μ is the linear density and v is the wave speed.

The speed of a wave can be determined if the frequency and wavelength of a harmonic are known, using v = λf.

Understanding the properties and equations of standing waves is crucial for solving wave-related physics problems and comprehending wave behavior.

Transcripts

Browse More Related Video

Standing Waves

AP Physics 1 - Standing Waves in Instruments

High School Physics - Standing Waves

Harmonics

AP Physics Workbook 10.J Standing Waves in Tubes

The Physics of Music: Crash Course Physics #19

Related Tags

Physics Education Wave Mechanics Standing Waves String Vibration Wave Frequencies Wave Patterns Mathematical Analysis Acoustics Harmonics Wave Speed