AP Physics 1 - Standing Waves in Instruments

Dan Fullerton
9 Jan 201414:24
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of standing waves in musical instruments, explaining how they are created and utilized in string and tube instruments. It covers the fundamental frequency and harmonics, detailing the mathematical relationships between string length, wavelength, and frequency. The script also addresses the differences between open and closed tube instruments, providing equations for calculating frequencies and wavelengths. It includes practical examples, such as designing a guitar string for a specific frequency and calculating frequencies and wavelengths for organ pipes. The video concludes with a problem on creating an A note in an open-ended tube instrument, encouraging further exploration of standing waves in music.

Takeaways
  • 🎵 Standing waves in instruments are created by fixing string ends or confining air in tubes, which allows for the formation of harmonics and overtones.
  • 🌟 The fundamental frequency in string instruments is set up by holding a string at both ends, creating a half-wavelength between the nodes.
  • 📶 The first harmonic corresponds to a full wavelength on the string, with the string length (L) being half the wavelength (λ) multiplied by the harmonic number (n).
  • 🔄 The frequency of each harmonic can be calculated using the wave speed (V), the string length (L), and the harmonic number (n) through the equation F = nV/(2L).
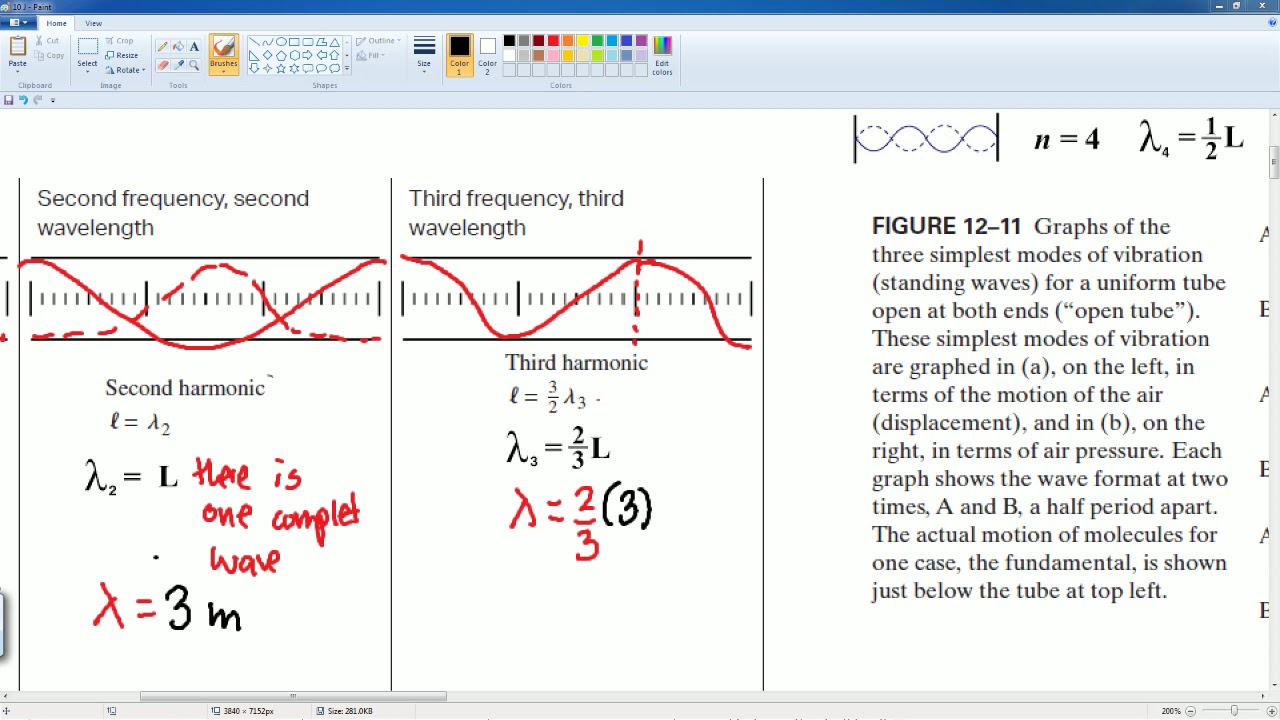
  • 🎷 Open-ended tube instruments like trumpets and flutes require an anti-node at each end, influencing the harmonics and overtones produced.
  • 🎹 Closed-ended tube instruments, such as some in pipe organs, form only fundamental frequency and odd harmonics due to the node at the closed end and anti-node at the open end.
  • 📐 The wavelength (λ) in a closed-ended tube is calculated as 4L/n, where L is the length of the tube and n is the harmonic number.
  • 🎸 For a guitar string, the length (L) can be determined by rearranging the frequency equation and solving for L, using the wave speed (V) and the desired fundamental frequency (F).
  • 🎺 In organ pipes, the highest and lowest frequencies, as well as the longest and shortest wavelengths, can be calculated by applying the appropriate equations for closed and open-ended tubes.
  • 🎻 To design a custom instrument with a specific fundamental frequency, the musician must use the correct equations for the type of tube (open or closed-ended) and solve for the required dimensions based on the speed of sound in air.
  • 🔗 For further understanding of standing waves, additional resources are available online, such as at 'aplusphysics.com'.
Q & A

  • What is a standing wave and how is it created in string instruments?

    -A standing wave is a wave pattern that appears to stand still, and it is created in string instruments by fixing the ends of the string, allowing only specific wavelengths to form due to the fixed ends acting as nodes. This principle is used in instruments like pianos, basses, cellos, violins, and guitars.

  • What is the fundamental frequency in string instruments, and how is it established?

    -The fundamental frequency in string instruments is the lowest frequency at which the string can vibrate. It is created by holding the string at both ends and setting up a half wavelength between the nodes, which are the fixed ends. This frequency is also known as the first harmonic.

  • How do overtones and harmonics relate to the wavelengths in a string?

    -Overtones and harmonics are higher frequencies that are integer multiples of the fundamental frequency. They are produced when the string vibrates in multiple sections, corresponding to whole number wavelengths. For example, a full wavelength (N=2) produces the second harmonic, and one and a half wavelengths (N=3) produce the third harmonic, and so on.

  • What is the relationship between the length of a string, its harmonic number, and the resulting frequency?

    -The length of the string (L) is related to the harmonic number (n) and the wavelength (λ) by the equation L = n * λ/2. The frequency (F) can then be found using the wave speed (V) and the length of the string with the equation F = n * V / (2 * L).

  • How do standing waves form in tubes, and what factors determine the wavelengths and frequencies?

    -Standing waves in tubes are formed by the reflection of sound waves between the ends of the tube. The wavelengths and frequencies are determined by the size of the tube and whether it is open or closed at the ends. For open-ended tubes, a node is required at each end, while closed-ended tubes must have a node at the closed end and an antinode at the open end.

  • What is the difference between the frequencies produced by closed-ended and open-ended tube instruments?

    -Closed-ended tube instruments can produce both fundamental frequencies and odd harmonics, while open-ended tube instruments can produce all harmonics including even ones. This is because closed-ended tubes must have a node at the closed end, which limits the vibration patterns and hence the frequencies that can be produced.

  • How can you calculate the length of a string needed to produce a specific fundamental frequency?

    -To calculate the length of a string for a specific fundamental frequency, use the equation L = n * V / (2 * F), where n is the harmonic number (1 for the fundamental frequency), V is the wave speed, and F is the frequency. Rearrange the equation to solve for L and plug in the known values.

  • What is the highest and lowest frequency observed in the organ pipes example?

    -In the organ pipes example, the highest frequency is observed in pipe number 3, and the lowest frequency is in pipe number 1. This is due to the different lengths and the harmonics at which each pipe is vibrating.

  • What are the longest and shortest wavelengths shown in the pipes?

    -The longest wavelength is observed in pipe number 1, and the shortest wavelength is in pipe number 3. This is because the wavelength is inversely proportional to the frequency for a given speed of sound, and the frequencies in these pipes vary.

  • How would you design a custom instrument with a tube open at both ends to produce an A note at 440 Hz as the fundamental frequency?

    -To design a custom instrument with a tube open at both ends to produce an A note at 440 Hz, use the equation for the frequency in an open-ended tube: F = n * V / (2 * L). Since n is 1 for the fundamental frequency, V is the speed of sound in air (343 m/s), and F is 440 Hz, you would solve for L to find the required tube length.

  • What is the length of the tube needed to produce an A note at 440 Hz in an open-ended tube instrument?

    -To produce an A note at 440 Hz in an open-ended tube instrument, the required tube length can be calculated using the equation L = n * V / (2 * F). With n as 1, V as 343 m/s, and F as 440 Hz, the calculation yields a tube length of approximately 0.39 meters.

  • What additional resources can one explore to learn more about standing waves?

    -For more information on standing waves, one can refer to educational resources such as physics textbooks, online physics courses, or websites dedicated to physics education, including 'aplusphysics.com' as mentioned in the transcript.

Outlines
00:00
🎶 Understanding Standing Waves in String Instruments

This paragraph introduces the concept of standing waves in string instruments, explaining how they are created by fixing a string at both ends to form nodes, which allows specific wavelengths to resonate. It mentions various stringed instruments like piano, bass, cello, violin, and guitar that utilize this principle to produce harmonics and overtones. The fundamental frequency is established by setting up a half-wavelength between the nodes, also known as the first harmonic. The paragraph further discusses the mathematical relationships between the harmonic, string length, wavelength, and resulting frequency, and how these can be used to determine the notes produced by the strings.

05:04
🎵 Frequency and Wavelength in Open and Closed Tubes

The second paragraph delves into the formation of standing waves in open and closed tubes, which is applicable to different types of musical instruments. It explains how the size of the tube and the movement of air within it determine the wavelengths and frequencies of the sound waves. The paragraph distinguishes between instruments with tubes open at both ends, like trumpets and flutes, and those with closed ends, like clarinets and some pipe organs. It also provides equations for calculating wavelengths and frequencies in closed-ended tubes, highlighting that only fundamental frequency and odd harmonics are allowed in such instruments.

10:05
🎼 Solving Problems with Standing Wave Principles

This paragraph presents practical problems related to the design of musical instruments, using the principles of standing waves. It includes a step-by-step explanation of how to calculate the required length of a guitar string to produce a specific frequency, and how to determine the highest and lowest frequencies and the longest and shortest wavelengths in a set of organ pipes. The paragraph concludes with a problem about designing a custom instrument with a tube open at both ends, explaining how to calculate the tube length to achieve a desired fundamental frequency of 440 Hertz, which corresponds to the musical note A.

Mindmap
Keywords
💡Standing Waves
Standing waves are a particular pattern of wave vibration that occurs when waves reflect back and forth between two fixed points, creating nodes (points of no displacement) and anti-nodes (points of maximum displacement). In the context of the video, standing waves are used to explain the principles behind the sound production in musical instruments, particularly stringed and wind instruments.
💡Nodes
Nodes are points in a standing wave pattern where there is no displacement; effectively, they are the points of minimum amplitude. In musical instruments, nodes are crucial for the formation of standing waves. The video explains that in string instruments, the ends held in place serve as nodes, which is essential for the creation of standing waves and, consequently, the production of sound.
💡Harmonics
Harmonics refer to the multiple frequencies that are integer multiples of a fundamental frequency. In musical instruments, the harmonic series is the sequence of frequencies that can be heard when a single note is played. The video explains how different harmonics are produced in string and tube instruments by varying the wavelength of the standing waves.
💡Wavelength
Wavelength is the distance between two successive points in a wave that are in phase, typically measured as the distance between two consecutive crests or troughs. In the context of the video, the wavelength is critical in determining the frequency of the sound produced by the standing waves in both string and tube instruments.
💡Frequency
Frequency refers to the number of cycles of a wave that occur in a unit of time, typically measured in Hertz (Hz). In musical terms, frequency corresponds to the pitch of a sound. The video discusses how the frequency of a standing wave is determined by the wavelength, the speed of the wave, and the length of the string or tube in the instrument.
💡Wave Speed
Wave speed is the rate at which a wave or disturbance travels through a medium, such as air or a string. In musical instruments, the wave speed affects the frequency of the sound produced by the standing waves. The video explains how the speed of the waves on a string can be manipulated to produce different musical notes.
💡Open-Ended and Closed-Ended Tubes
These terms refer to the types of tubes used in wind instruments. An open-ended tube is one that is open at both ends, while a closed-ended tube is sealed at one end. The distinction is important because it affects the formation of standing waves and the frequencies and wavelengths produced. Open-ended tubes allow for the formation of both odd and even harmonics, while closed-ended tubes produce only odd harmonics.
💡Anti-Nodes
Anti-nodes are points in a standing wave pattern where the displacement is at a maximum. In musical instruments, anti-nodes are points of maximum vibration and are essential for the propagation of sound waves. The video discusses the role of anti-nodes in the formation of standing waves in wind instruments.
💡Fundamental Frequency
The fundamental frequency is the lowest frequency of a sound wave and is the first harmonic in a series of overtones. In musical instruments, it is the primary pitch that we perceive when a note is played. The video explains that the fundamental frequency is created when a string or tube is set up with half a wavelength between the nodes.
💡Overtones
Overtones are additional frequencies that accompany the fundamental frequency in a musical note. They are the higher harmonics that give a note its characteristic timbre or quality. The video discusses how overtones are produced in string and tube instruments by the formation of standing waves with varying wavelengths.
💡Wave Equation
The wave equation is a fundamental equation in physics that describes how waves propagate through a medium. It relates the speed of the wave, its frequency, and its wavelength. In the context of the video, the wave equation is used to derive the formulas for calculating the frequencies and wavelengths of standing waves in musical instruments.
💡Guitar Designer
A guitar designer is a professional who designs and creates guitars, taking into account the physical principles of sound production to ensure the instrument produces the desired tones and is playable. The video provides an example of a guitar designer applying the principles of standing waves to design an instrument that produces a specific frequency.
Highlights

Standing waves can be created in instruments by holding a string at both ends and introducing a disturbance.

The ends of the string that are held in place serve as nodes, allowing only certain wavelengths to form within the string.

Many stringed instruments like piano, bass, cello, violin, and guitar utilize the principle of standing waves to produce harmonics and overtones.

The fundamental frequency in string instruments is created by setting up a half wavelength between the nodes at both ends of the string.

The frequency of each harmonic can be determined by a set of relationships involving the harmonic, string length, wavelength, and resulting frequency.

The equation for the length of the string is L = n * λ/2, where L is the length, n is the harmonic number, and λ is the wavelength.

The frequency of each harmonic in a string can be found using the wave equation, which relates wave speed (V), wavelength (λ), and frequency (F).

For open and closed tubes, the wavelengths and frequencies are produced differently, with the size of the tube and the movement of air playing crucial roles.

Instruments like trumpets, pipe organs, flutes, clarinets, and oboes, which are open at both ends, require an anti-node at each end for the formation of standing waves.

Closed-ended tube instruments, such as the clarinet, can only form the fundamental frequency and odd harmonics due to the presence of a node at the closed end and an anti-node at the open end.

The wavelength and frequency equations for a tube closed at one end are λ = 4L/n and F = nV/(4L), with n taking odd integer values.

A guitar designer aiming for a first fundamental frequency of F# at 370 Hz with a wave speed of 450 m/s can calculate the required string length using the equation F = nV/(2L).

The length of a string needed for the F# note at 370 Hz with a wave speed of 450 m/s is approximately 0.61 meters.

In a set of organ pipes, the highest and lowest frequencies and the longest and shortest wavelengths can be determined by applying the appropriate equations for closed and open-ended tubes.

Pipe number 3 has the highest frequency and the shortest wavelength, while pipe number 1 has the lowest frequency and the longest wavelength.

A musician designing a custom instrument with a tube open at both ends can calculate the tube length required to produce a fundamental frequency of A (440 Hz) using the equation F = nV/(2L) with n being the first harmonic.

The required length of the tube for the custom instrument to produce an A note at 440 Hz is approximately 0.39 meters.

For more information on standing waves, readers are directed to a physics resource website.

Transcripts

Browse More Related Video

AP Physics Workbook 10.J Standing Waves in Tubes

Standing Waves on a String, Fundamental Frequency, Harmonics, Overtones, Nodes, Antinodes, Physics

Standing Waves

The Physics of Music: Crash Course Physics #19

A better description of resonance

Harmonics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Standing WavesMusical InstrumentsString TheoryTube ResonanceHarmonic FrequenciesSound CreationPhysics of MusicAcoustic PrinciplesWave EquationsInstrument Design